【洛谷】【P5782】和平委员会（2—SAT问题，tarjan算法）

传送门：和平委员会        2-SAT问题详解        tarjan算法

---

题目描述

根据宪法，Byteland 民主共和国的公众和平委员会应该在国会中通过立法程序来创立。 不幸的是，由于某些党派代表之间的不和睦而使得这件事存在障碍。 此委员会必须满足下列条件：

• 每个党派都在委员会中恰有 1 个代表。
• 如果 2 个代表彼此厌恶，则他们不能都属于委员会。

每个党在议会中有 2 个代表。代表从 1 编号到 2n。 编号为 2i−1 和 2i 的代表属于第 i 个党派。

任务：写一程序读入党派的数量和关系不友好的代表对，计算决定建立和平委员会是否可能，若行，则列出委员会的成员表。

---

输入格式

第一行有两个非负整数 n,m。他们各自表示：党派的数量 n 和不友好的代表对 m。

接下来 m 行，每行为一对整数 a,b，表示代表 a 和 b 互相厌恶。

---

输出格式

如果不能创立委员会，则输出信息 NIE。

若能够成立，则输出包括 n 个从区间 1 到 2n 选出的整数，按升序写出，每行一个，这些数字为委员会中代表的编号。

如果委员会能以多种方法形成，程序可以只输出它们的某一个。

---

题解

这一道题就是经典的2-SAT板子题，先看一下我对2-SAT问题的理解和思路

讲一下代码思路：

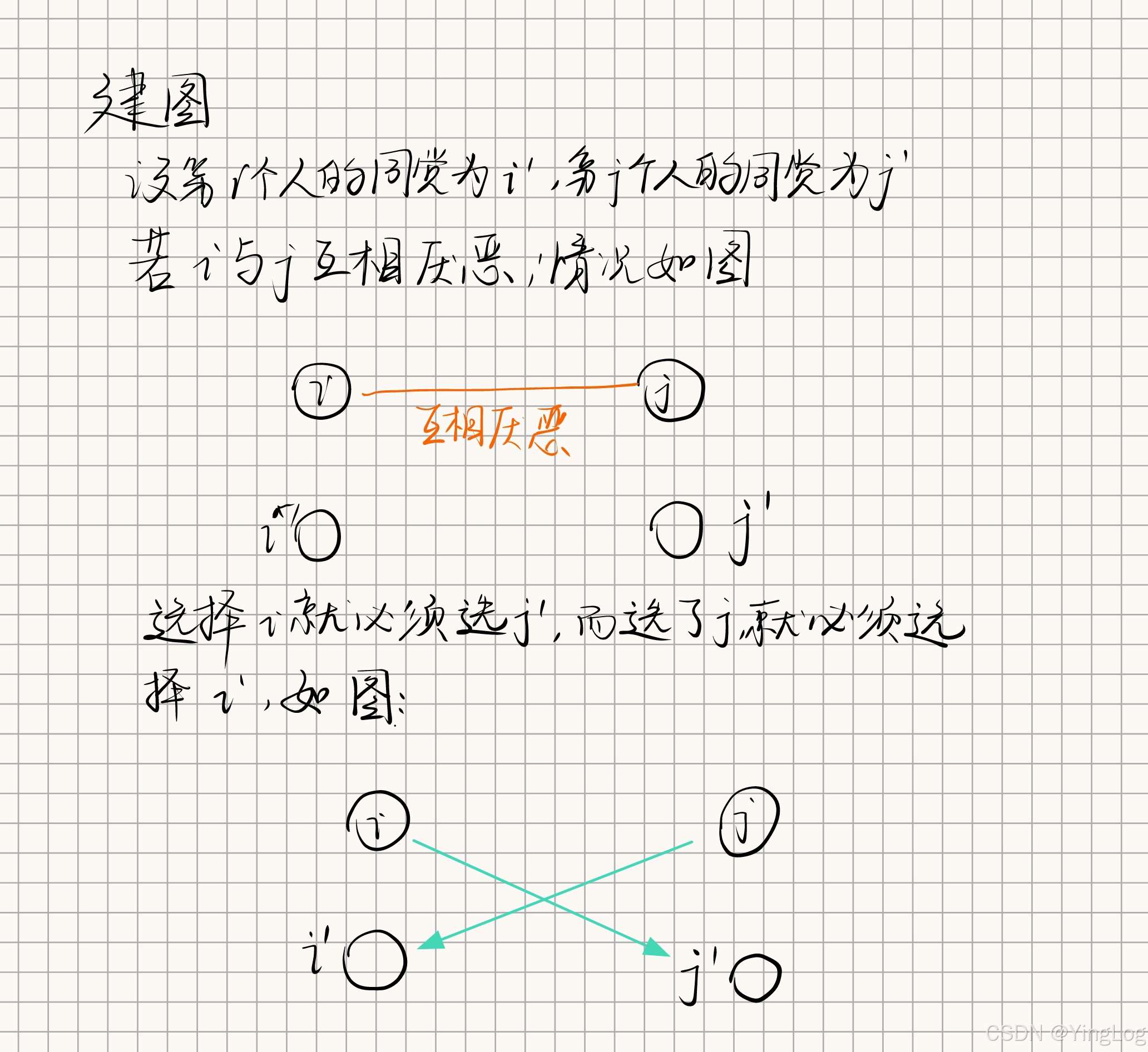
• partner(int x):
  用于返回节点 x 的伙伴节点。奇数节点返回其加一的偶数，偶数节点返回其减一的奇数。

• tarjan(int u, int fa):
  这是实现 Tarjan 算法的核心递归函数。它用于深度优先遍历（DFS）并标记每一个节点 u 的 dfn（深度优先序列编号）和 low（可以追溯到的最小 dfn 编号）。

  • 如果未遍历节点 v（!dfn[v]），则递归调用 tarjan。
  • 如果 v 已经被访问且不在当前强连通分量中，则更新 low[u]。
  • 当low[u] 与 dfn[u] 相等时，表示找到了一个强连通分量，通过弹栈的方式将该强连通分量内的节点标记为相同的编号。

• 
  

在 main() 函数中：

1. 读取节点 n 和边 m 的数量。
2. 构建图 t，对于每一条边 (a, b)，将边的伙伴节点添加到图中。
3. 遍历所有节点，调用 tarjan 对未被访问的节点进行处理。
4. 在所有节点中，检查每对伙伴节点是否属于同一强连通分量。
   • 如果存在一对伙伴节点属于同一强连通分量，输出 "NIE" （代表不可以有效配对），然后返回。
5. 如果检查通过，对于每一对伙伴节点，根据其强连通分量的编号输出结果。（强连通分量的编号呈逆拓扑排序）

#include <bits/stdc++.h>
using namespace std;
const int M=2e5+5;
#define endl '\n'
int partner(int x){
    return (x%2)?x+1:x-1;
}
vector<int>t[M];
int dfn[M],low[M],cur;
int num[M],num_cnt;
stack<int>st;
void tarjan(int u,int fa){
    dfn[u]=low[u]=++cur;
    st.push(u);
    for(int i=0;i<t[u].size();i++){
        int v=t[u][i];
        if(!dfn[v]){
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
        }
        else if(!num[v]){
            low[u]=min(low[u],dfn[v]);
        }
    }
    if(low[u]==dfn[u]){
        num[u]=++num_cnt;
        while(st.top()!=u){
            num[st.top()]=num_cnt;
            st.pop();
        }
        st.pop();
    }
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int a,b;
        cin>>a>>b;
        t[a].push_back(partner(b));
        t[b].push_back(partner(a));
    }
    for(int i=1;i<=2*n;i++){
        if(!dfn[i]){
            tarjan(i,-1);
        }
    }
    for(int i=1;i<=2*n;i+=2){
        if(num[i]==num[i+1]){
            cout<<"NIE";
            return 0;
        }
    }
    for(int i=1;i<=2*n;i+=2){
        if(num[i]<num[i+1]){
            cout<<i<<endl;
        }
        else cout<<i+1<<endl;
    }
    return 0;
}

---