3.二次代价函数，梯度下降法找loss最小值，交叉熵函数 的应用

二次代价函数(quadratic cost)

** 其中，C表示代价函数，x表示样本，y表示实际值，a表示输出值，n表示样本的总数。**

• 为简单起见，同样一个样本为例进行说明，此时二次代价函数为：
  
  y是label，是已知的， z是信号的总和。a是预测值（是需要计算的）等于z的信号总和之后的激活函数
  y-a表示真实值与预测值之间的差值
  相当于loss = tf.reduce_mean(tf.square(y - prediction)) ，需要的是越小越好。
  train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss)

---

梯度下降法（Gradient descent）找最低点（loss的最小值）

从以上公式可以看出，w和b的梯度跟激活函数的梯度成正比，激活函数的梯度越大，w和b的大小调整得越快，训练收敛得就越快。

最好是：在远离最低点的时候，导数要越大越好，在离最低点近的时候，导数越来越小

---

换一个思路，我们不改变激活函数，而是改变代价函数，改用交叉熵函数

其中C表示代价函数，x表示样本，y表示实际值，a表示预测值，n表示样本的总数

sigmoid函数为：

可证：

求w的最小值，两边对w进行求导

求b的最小值

---

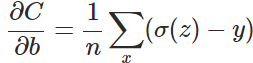
总结：

</