八股文——机器学习基础损失函数

一、常见的代价函数

1、二次代价函数

J=1/2nΣ||a(x)-y(x)||^2

对于一个样本而言，J=(y-a)/2

激活函数的梯度越大，权值w和b大小调整的越快，训练收敛的越快

假使激活函数是sigmoid函数，当使用二次代价函数时，很可能会出现梯度消失，使用sigmoid函数在饱和区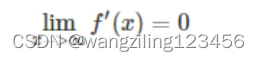即x过大或者过小时，梯度是接近于0

2.交叉熵代价函数

J=-1/nΣ[yln(a)+(1-y)ln(1-a)]

更适合搭配sigmoid激活函数

二、常见的损失函数

1.用于回归

绝对值损失函数和平方损失函数

绝对值损失函数MAE

平方损失函数MSE

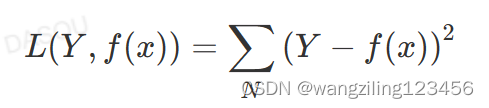
 MSE比MAE可以更快的收敛，当使用梯度下降算法时，MSE梯度下降是变化的，MAE梯度损失是均匀不变的，梯度不发生改变不利于模型的训练（调节学习率）。