LeetCode42 接雨水_42. 接雨水-优快云博客

本文链接：https://blog.youkuaiyun.com/zjsru_Beginner/article/details/122793214

该博客讨论了一个计算雨水收集问题的算法，通过分析柱状图的高度来确定能够收集到的雨水量。作者首先提出了两种方法：按行求解和按列求解。按行求解的时间复杂度过高，不适合大数据量；而按列求解的方法通过找到每列的左右最高柱子来计算雨水，但这种方法在某些测试用例中仍存在效率问题。为了优化，作者进一步改进了算法，通过一次遍历计算左右最大高度，从而减少了重复搜索，提高了效率。代码实现中涉及到了动态维护最大值的概念。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

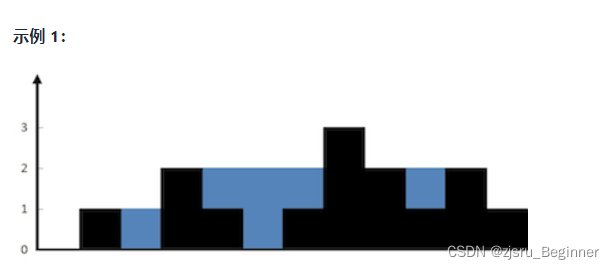
示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105

看到这个图片大致就了解这个题目时什么意思了，一开始蹦出了两个想法，一个是按照行去求。

从行的方式求解

由图可以看出来要收集到雨水的条件为左右都有墙壁，形成一个左右密封的区域，所以可以通过一行一行的来判断，但是时间复杂度为m*n，m为其中最高的柱子高度，n为柱子个数，从最后的结果来看，最后两个测试样例没有办法通过，因此不主要写行的求法

从列的方式求解

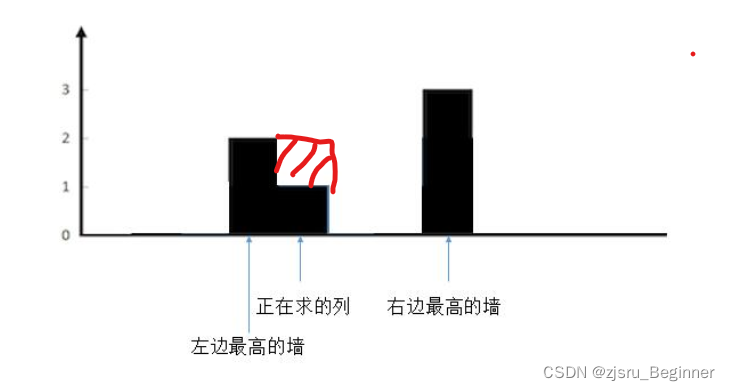
求每一列的水，我们只需要关注当前列，以及左边最高的柱子，右边最高的柱子就够了。

装水的多少，当然根据木桶效应，我们只需要看左边最高的柱子和右边最高的柱子中较矮的一个就够了。

所以，我们可以通过循环来寻找左边和右边最高的柱子（图中红色部分为改列收集到的水）

class Solution {
public:
    int trap(vector<int>& height) {
        int leftmax,rightmax,i,j,sum;
        sum=0;
        for (int i = 1; i < height.size()- 1; i++) {   //因为最左和最右的格子一定无法收集到水因此不去考虑
             leftmax = 0;
            for (j = i - 1; j >= 0; j--) {    //通过循环寻找左边的最高的柱子
            if (height[j] > leftmax) {
                leftmax = height[j];
                }
            }
            rightmax = 0;
            for (j = i + 1; j < height.size(); j++) {  //通过循环寻找右边最高的柱子
                if (height[j] > rightmax) {
                rightmax = height[j];
                }
            }
            int minnumber =min(leftmax,rightmax);   //通过比较获得较短的那一条边
             if (minnumber > height[i]) {
            sum = sum + (minnumber - height[i]);   //减去自生的高度，就可以得到收集到的水
            }
        }
        return sum;
    }

};

经过代码提交发现最后有一个测试点没有办法通过，考虑对代码进行优化，分析超时的原因为每次都需要对选择柱子的前后进行查找最大，当数据过于庞大的时候会比较浪费时间，进行改进

将原来的leftmax和rightmax改为数组，通过一次整体的遍历可以将每个的点的左最大和右最大找到

class Solution {
public:
    int trap(vector<int>& height) {
        int i,number,sum;
        sum=0;
        number=height.size();
        vector<int> leftmax(number);   //我在自己的软件中跑时使用数组的可以成功的，但是不知道为啥平台里需要用到容器
        vector<int> rightmax(number);
        for (i = 1; i < number - 1; i++) {
            leftmax[i] = max(leftmax[i - 1], height[i - 1]);  //改列的左最大为前一列的左最大和前列进行比较取最大值
        }
        for (i = number - 2; i > 0; i--) {
            rightmax[i] = max(rightmax[i + 1], height[i + 1]);  ////改列的右最大为后一列的右最大和后列进行比较取最大值
        }
        for (i = 1; i < number - 1; i++) {
            int minnumber = min(leftmax[i], rightmax[i]);
            sum += max(0, minnumber - height[i]);
        }
        return sum;
    }
};

soy