poj1548机器人

题目描述：贵公司提供的机器人可用于在体育赛事和音乐会后从田间捡拾垃圾。在机器人被分配到工作之前，田野的航拍照片用网格标记。网格中包含垃圾的每个位置都被标记。所有机器人都从西北角开始，在东南角结束运动。机器人只能向东或南两个方向移动。进入包含垃圾的牢房后，机器人将在继续之前将其捡起。一旦机器人到达东南角的目的地，它就不能重新定位或重复使用。由于您的费用与用于特定工作的机器人数量成正比，因此您有兴趣找到可以清洁给定场地的最少机器人数量。例如，考虑图 1 中所示的字段映射，其中行和列的编号如图所示，垃圾位置标有“G”。在此方案中，所有机器人都将从位置 1,1 开始，并在位置 6, 7 结束。

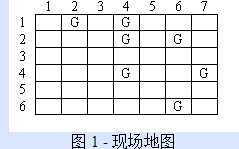
下面的图 2 显示了两种可能的解决方案，其中第二种更可取，因为它使用两个机器人而不是三个。

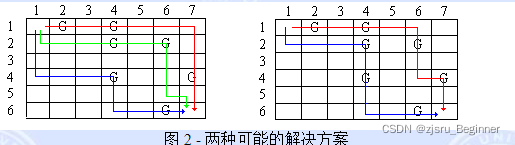
您的任务是创建一个程序，该程序将确定从田地中拾取所有垃圾所需的最少机器人数量。

问题分析：题目的意思是一个矩形区域，在若干个给定的坐标上有垃圾。机器人从西北角（矩形区域的左上角）开始清理，它只能向东或者向南行进，如果到达了东南角（矩形区域的右下角）则完成了它的使命。问最少用多少个机器人可以将所有的垃圾清理完毕。然后用Dilworth定理，把坐标看成一对数组，也就是求这个数组的最长反链。实际上这样一看，与poj1065的题意如出一辙。先排序，然后求最长下降子序列。

代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define N 28
typedef struct node{         //定义坐标数组
    int a,b;
}node;
node p[N*N];
int dp[N],n=0,len=0,a,b;
int cmp(const void *a,const void *b){
    if((*(node *)a).a == (*(node *)b).a) 
        return (*(node *)a).b - (*(node *)b).b;     //比较函数，按照降序排序
    return (*(node *)a).a - (*(node *)b).a;
}
int find (int x,int len){
    int low,high,mid;
    low = 0;
    high = len;
    while(low <= high){
        mid = (low+high)>>1;            //二分查找排序
        if(dp[mid] == x)
            return mid;
        else if(dp[mid] > x)
            low = mid+1;
        else
            high = mid-1;
    }
    return low;
}
int main(){
    while(scanf("%d %d",&a,&b) &&a!=-1&&b!=-1){
        int i,j;
        if(a && b){
            p[n].a = a;
            p[n++].b = b;
            continue;
        }
        qsort(p,n,sizeof(node),cmp);    //将node排序
        for(i = 0;i<n;i++){
            j = find(p[i].b,len);
            if(j == len+1)
                dp[++len] = p[i].b;
            else
                dp[j] = p[i].b;
        }
        printf("%d\n",len+1);
        n = 0;
        len = 0;
        memset(dp,0,sizeof(dp));
    }
    return 0;
}

yjg