进制转换相关问题（包括51常用的二进制，八进制，十进制，十六进制等等）

我们日常生活中使用最多的就是十进制，那我们以此为切入点：

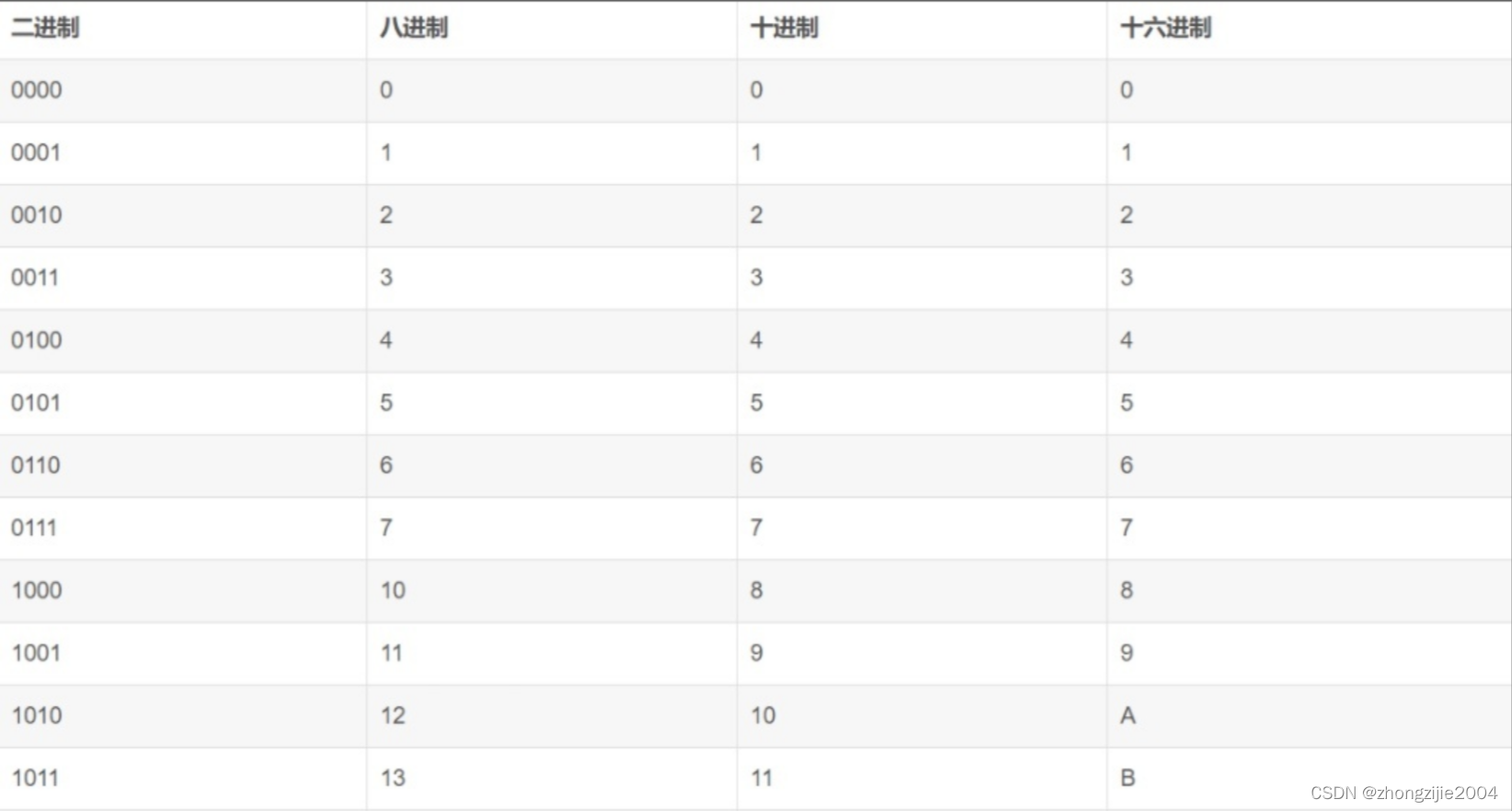
 整型有4种进制形式：
1.十进制： 以0-9这九个数字组成，不能以0开头；
2.二进制： 以0和1两个数字组成；
3.八进制： 以0-7数字组成，为了区分与其他进制的数字区别，开头都是以0开始；
4.十六进制：以0-9和A-F组成，为了区分于其他数字的区别，开头都是以0x开始。

  

​​​​​​一.十进制转换为二进制，八进制，十六进制；

十进制转二进制：

 将一个十进制数除2得到的整数部分保留，作为第二次除2时的被除数，得到的余数依次记下，重复上述步骤，直到整数部分为0就结束，将所有得到的余数最终逆序输出，则为该十进制对应的二进制数

 9（10）=1001（2）

 十进制转八进制或者十六进制：

与十进制转二进制的原理类似，除以8或者16，反向取余数，直到商为0终止。

需要特别注意的是，十六进制数是由0-9和A-F(或者a-f)组成的，A相当于十进制中的10，B相当于11，依次类推，F相当与15，上述事例中取得的余数12即为十六C。

我们不难得出规律：以上几种进制的整数部分转换原理都是除进制数取余数，然后倒序输出。

 二.二进制，八进制，十六进制的转换；

二进制与八进制的相互转换：

我们都知道：2^3=8;

所以二进制与八进制的转换可以采用“对应法”，简单的来说，从低位开始，取二进制数中的每三位合为八进制数的一位，例如：

1010 0100（2）=244（8）

所以二进制转换为十六进制也是这个原理，因为2^4=16;所以从低位开始，取二进制数中的四位合为十六进制数的一位，例如：

1001 0001（2）=91（16）

 三.八进制与十六进制的相互转换：

这两者之间的转换可以借助十进制或者二进制完成（最好是二进制），可以先将八进制转换成十进制或二进制，再转换成十六进制，通过间接转换的方法来实现。

第一次写文章，有不对的地方请多多指点，如果对你有帮助请点个《赞》。