多目标鸟群算法研究

多目标鸟群算法

1 引言

许多实际优化问题涉及同时优化多个冲突目标。航空发动机设计、星座设计、跨模态检索、无人机和图像处理等领域均涉及多目标优化[1–5]。经典优化方法建议通过为目标添加权重向量，将多目标优化问题转化为单目标优化问题，然后每次寻找一个特定的帕累托最优解。基于单一最优解，某些目标得到改善的同时，其他目标会恶化。为应对这一难题，希望在每次仿真运行中都能找到折衷解。多目标进化算法（MOEAs）的发展为多目标优化问题提供了可行途径，例如NSGA‐II[6], MOPSO[7], PAES[8], 等。这些多目标进化算法（MOEAs）是基于种群的算法，继承了单目标算法的所有优良特性，使它们能够同时探索帕累托前沿的不同部分。

鸟群算法（BSA）是一种新的仿生优化算法（2015）[9]。该算法模拟鸟类的觅食行为、防御行为和飞行行为。该算法具有参数少、易于调节的优点。目前，该算法的改进工作主要集中在单目标优化问题上，迄今为止尚无文献报道用于处理多目标优化问题。因此，本研究将帕累托最优解引入鸟群算法，以期同时找到多个最优解。

2 鸟群算法简述

从鸟群的觅食、防御和飞行行为中，可以总结出五条规则[9]：（1）每只鸟在防御和觅食行为之间自由转换，这是一种随机行为。（2）在觅食过程中，每只鸟可以记录并更新自身关于食物的最优信息以及群体的最优信息，这些信息用于寻找新的食物来源。同时，整个群体共享社会信息。（3）在防御过程中，每只鸟试图向中心移动，但该行为受到群体内竞争的影响。警觉性高的鸟比警觉性低的鸟更有可能接近中心。（4）鸟群每次飞往另一个地点时，警觉性最高的鸟成为生产者，警觉性最低的鸟成为寄生者，警觉性介于两者之间的鸟则随机成为生产者或寄生者。（5）生产者主动寻找食物，而寄生者跟随生产者随机行动。上述五条规则的数学描述如下：

鸟群的大小为M，维度数量为N，$x^t_i$表示每只鸟的位置，其中t表示当前迭代次数，i = 1, 2,…, N。规则（2）中的觅食行为被表述为

$$
x^{t+1}_i = x^t_i + c_1 r_1 (p_i - x^t_i) + c_2 r_2 (g - x^t_i) \tag{1}
$$

$c_1$ 和 $c_2$ 是非负常数。$r_1$ 和 $r_2$ 是区间[0,1]内的随机数。$p_i$, $g$ 分别是第i只鸟的历史最优位置和整个鸟群的历史最优位置。

根据规则（3），鸟群中的鸟试图靠近中心区域，但鸟与鸟之间存在竞争关系。这些行为可以表示如下，

$$
x^{t+1} {i,j} = x^t {i,j} + A_1 r_3 (\text{mean} j - x^t {i,j}) + A_2 r_4 (p_{k,j} - x^t_{i,j}) \tag{2}
$$

$$
A_1 = a_1 \times e^{(- \frac{\text{pFit}_i}{\text{sumFit}} + \varepsilon \times N)} \tag{3}
$$

$$
A_2 = a_2 \times e^{\left( \frac{\text{pFit}_i - \text{pFit}_k}{|\text{pFit}_k - \text{pFit}_i| + \varepsilon} \times N \times \frac{\text{pFit}_k}{\text{sumFit}} + \varepsilon \right)} \tag{4}
$$

其中，$a_1$ 和 $a_2$ 是(0, 2)之间的常数，$\text{pFit}_i$ 表示第i只鸟的最优值，$\text{sumFit}$ 表示整个鸟群最优值的总和。$\varepsilon$ 是计算机能表示的最小实数。$\text{mean}_j$ 是第j维中位置的平均值。$r_3$ 是(0, 1)之间的随机数，$r_4$ 是(−1, 1)之间的随机数，k ≠ i。

根据规则（4），每隔一段时间FQ，鸟群可能会飞到另一个地方，一些鸟能够成为生产者，其他则会成为寄生者，生产者和寄生者的行为可被解释为，

$$
x^{t+1} {i,j} = x^t {i,j} + r_5 x^t_{i,j} \tag{5}
$$

$$
x^{t+1} {i,j} = x^t {i,j} + \text{FL} \cdot r_6 (x^t_{k,j} - x^t_{i,j}) \tag{6}
$$

$r_5$ 是满足方差为0、均值为1的高斯随机数。$r_6$ 是介于(0, 1)之间的随机数，FL表示寄生者跟随生产者。

3 多目标鸟群算法

3.1 多目标优化

多目标优化问题(MOOP)旨在找到一组可接受的解，这与只有一个解的单目标问题相反。多目标优化问题(MOOPs)中的解旨在在不同准则之间实现权衡，从而允许多个最优解的存在。MOOP的一般描述为，

$$
\min f(X) = [f_1(X), f_2(X), …, f_m(X)] \tag{7}
$$

$$
g_i(X) \leq 0, \quad i = 1, 2, …, k \tag{8}
$$

$$
h_i(X) = 0, \quad i = 1, 2, …, l \tag{9}
$$

其中，解向量 $X = [x_1, x_2, …, x_n]^T$，$f_i(X)$，i=1，2, …, m为目标函数。求解多目标优化问题的目标是获得尽可能多的帕累托最优解。

3.2 并行细胞坐标系(PCCS)

多目标优化问题涉及同时优化两个以上的目标。受平行坐标概念的启发，多维帕累托前沿可以转换为二维平面网格，同时保持笛卡尔坐标的相对位置关系。帕累托前沿的坐标通过公式(10)转换为整数值坐标，

$$
L_{k,m} = \text{ceil}\left(K \cdot \frac{f_{k,m} - f^{\min}_m}{f^{\max}_m - f^{\min}_m}\right) \tag{10}
$$

其中，k = 1,2, …, K，K为外部档案中帕累托解的数量。$f^{\min} m$ 和 $f^{\max}_m$ 分别为帕累托前沿上第m个目标的最小值和最大值。$L {k,m} \in [1,K]$ 为平行坐标系中 $f_{k,m}$ 的整数标签。如果 $f_{k,m} = f^{\min} m$，则 $L {k,m} = 1$。

3.3 外部档案更新

外部档案中的Pareto解通过其在PCCS中的密度进行评估。首先，将Pareto解投影到PCCS中，第i个解的密度定义如公式(11)所示。

$$
D(i) = \sum_{\substack{j=1 \ j \neq i}}^{K} \frac{1}{D_{pc}(i,j)^2} \tag{11}
$$

$D_{pc}(i,j)$ 表示两个不同帕累托解之间的平行单元距离。

$$
D_{pc}(i,j) =
\begin{cases}
0.5, & \text{if } \forall m, L_{i,m} = L_{j,m} \
\sum_{m=1}^{M} |L_{i,m} - L_{j,m}|, & \text{otherwise}
\end{cases} \tag{12}
$$

外部档案具有一个最大尺寸，该尺寸由用户设定，以反映期望的最终解的数量。新解是否为非支配解，将通过非支配排序方法[12]进行评估。

3.4 多目标优化的构建

$p_i$ 在公式(1)中是迄今为止第i个非支配解，而 $g$ 是从外部档案中选择的一个非支配解，其选择规则是 $g$ 位于PCCS中的低密度区域。$A_1$ 和 $A_2$ 在公式(2)中被修改为，

$$
A_1 = a_1 \times \left(- \sum_{m=1}^{M} \frac{\text{pFit}_{i,m}}{\text{sumFit}_m + \varepsilon} \times \text{pop} \times \frac{1}{M} \right) \tag{13}
$$

$$
A_2 = a_2 \times \left( \sum_{m=1}^{M} \left( \frac{\text{pFit} {i,m} - \text{pFit} {k,m}}{|\text{pFit} {k,m} - \text{pFit} {i,m}| + \varepsilon} \times \text{pop} \times \frac{\text{pFit}_{k,m}}{\text{sumFit}_m + \varepsilon} \right) \times \frac{1}{M} \right) \tag{14}
$$

其中，$\text{pFit}_{i,m}$ 表示第i只鸟的第m个目标的最优值。$\text{sumFit}_m$ 是第m个目标的适应度总和。pop为鸟的总数。M为目标数量。其他变量与公式(3)和(4)中的相同。

鸟群算法的基本规则(4)中只有一个适应度函数，容易判断最小值和最大值，但在多目标优化中需要评估多个目标，最优解指的是一组非支配解。在所提出的MOBSA中，鸟的当前位置将被划分为两部分：非支配解和被支配解。假设位置不被其他鸟支配的鸟为生产者，换句话说，位置被支配的鸟为寄生者。MOBSA的结构如图1所示。

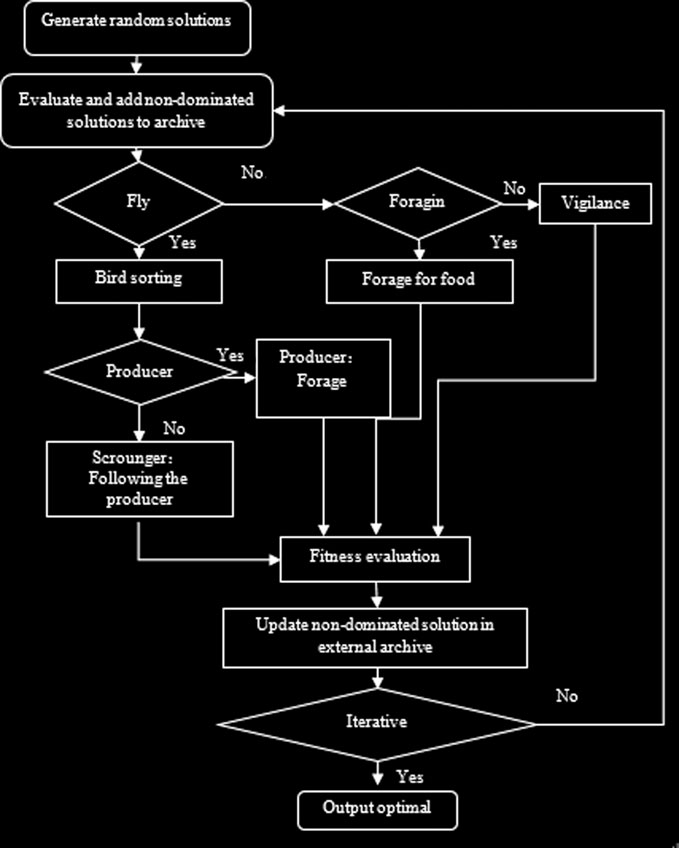
4 评估与分析

4.1 性能优点

多目标优化方法的收敛性能通常通过非支配解的数量、两组覆盖率、世代距离（GD, [10]）、最大帕累托前沿误差(ME)等指标进行评估[6, 10, 11]。本文使用的收敛性性能指标是GD，GD值越小，表示向帕累托前沿的收敛性越好。实验中使用的第二类性能指标是两组覆盖率和间距指标，通常通过分布函数$\Delta$来估算。

$$
\text{GD} = \frac{\left(\sum_{i=1}^{n’} d_i^p \right)^{1/p}}{n’} \tag{15}
$$

其中，$n’$为找到的非支配解的数量，$d_i$为使用算法获得的每个帕累托解到真实帕累托解的欧几里得距离，其公式见式(16)。如果所获得的解位于已知的帕累托最优前沿上，则$d_i = 0$。

$$
d_i = \min_j \sqrt{\sum_{k=1}^{M} (f^i_k - f^j_k)^2} \tag{16}
$$

$n$为已知非支配解的数量，$f^i_k$表示第$i$个个体的第$k$个目标值。

$$
\Delta = \frac{\sum_{m=1}^{M} d^e_m + \sum_{i=1}^{N-1} |d_i - \bar{d}|}{\sum_{m=1}^{M} d^e_m + (n - 1)\bar{d}} \tag{17}
$$

其中，$d_i$ 是所获得的帕累托最优解集中相邻解之间的欧几里得距离。$d^e_m$ 是极端解与所找到的非支配解集在第$m$个目标分量上的边界解。$\bar{d}$是所有$d_i$的平均值。如果获得的解均匀分布良好，即$d_i = \bar{d}$，并且所获得帕累托前沿上的极端解与真实帕累托前沿上的极端解重合，$\Delta = 0$，否则$\Delta > 0$。$\Delta$越小，帕累托前沿分布越好。

4.2 测试函数

使用了四个无约束测试问题来评估MOBSA、NSGA‐II和MOPSO。SCH函数是由Schaffer（1985年）提出并被几乎所有MOEA使用的最常见问题。本研究还测试了FON函数[13]。ZDT3和ZDT6（Zitzler等人）被采纳为测试函数。所有问题均具有两个目标。其他详细信息见表1。由于MOPSO和MOBSA在粒子数量较少时偶尔无法正常工作，因此SCH函数的种群规模设置为500。外部存档库的容量为100。对于MOBSA，鸟的种群数量为50。$c_1 = c_2 = 1.5$，$a_1 = a_2 = 1$，$P \in [0.8, 1]$，$\text{FL} \in [0.5, 0.9]$，$\text{FQ} = 10$。MOPSO的群体也包含50个个体。解空间被划分为49个超立方体。$\omega \in [0.5, 0.9]$，$r_1 = r_2 = \text{rand}$。至于NSGA‐II，种群规模为100，竞赛规模设置为2[12–14]。

表1 测试问题

问题	函数	维度 $n$	边界	最优解	帕累托前沿描述
FON	$f_1(x) = 1 - \exp\left(-\sum_{i=1}^{n} (x_i - \frac{1}{\sqrt{n}})^2\right)$ $f_2(x) = 1 - \exp\left(-\sum_{i=1}^{n} (x_i + \frac{1}{\sqrt{n}})^2\right)$	3	$[-4, 4]$	$x_1 = x_2 = x_3 \in [-1/\sqrt{3}, 1/\sqrt{3}]$	非凸
SCH	$f_1(x) = x^2$ $f_2(x) = (x - 2)^2$	1	$[-10^3, 10^3]$	$x \in [0, 2]$	凸
ZDT3	$f_1(x) = x_1$, $f_2(x) = g \cdot h$ $g = 1 + 9 \sum_{i=2}^{n} x_i / (n-1)$ $h = 1 - \sqrt{f_1/g} - (f_1/g)\sin(10\pi f_1)$	10	$[0, 1]$	$x_1 \in [0, 0.0830015349] \cup [0.1822287280, 0.257762334] \cup [0.4093136748, 0.4538821041] \cup [0.6183967944, 0.6525117038] \cup [0.8233317983, 0.8518328654]$ $g(x) = 1$	断开连接，凸
ZDT6	$f_1(x) = 1 - e^{-4x_1} \sin^6(6\pi x_1)$ $f_2(x) = g \cdot h$ $g = 1 + 9 \left[\sum_{i=2}^{n} x_i / (n-1)\right]^{0.25}$ $h = 1 - (f_1/g)^2$	10	$[0, 1]$	$x_1 \in [0.2807753191, 1]$ $g(x) = 1$	非均匀间隔，非凸

表2 SCH函数的性能优点（GD，$\Delta$）

算法	GD Max	GD Min	GD AVE	GD Sd.	$\Delta$ Max	$\Delta$ Min	$\Delta$ AVE	$\Delta$ Sd.
多目标粒子群优化	5.10E−03	4.40E−03	4.70E−03	2.21E−04	0.992	0.857	0.912	0.034
非支配排序遗传算法II	0.025	4.40E−03	0.006	2.21E−04	0.992	0.802	0.883	0.134
MOBSA	4.80E−03	4.50E−03	4.65E−03	2.21E−04	0.992	0.637	0.679	0.025

表3 FON函数的性能优点（世代距离，$\Delta$）

算法	GD Max	GD Min	GD AVE	GD Sd.	$\Delta$ Max	$\Delta$ Min	$\Delta$ AVE	$\Delta$ Sd.
多目标粒子群优化	6.98E−04	4.09E−04	4.65E−04	6.06E−05	0.928	0.851	0.882	0.019
非支配排序遗传算法II	0.004	4.32e−04	0.001	6.06E−05	0.928	0.851	0.882	0.090
MOBSA	5.32E−04	4.49e−04	4.98e−04	6.06E−05	0.928	0.851	0.882	0.019

表4 ZDT3函数的性能优点（世代距离，$\Delta$）

算法	GD Max	GD Min	GD AVE	GD Sd.	$\Delta$ Max	$\Delta$ Min	$\Delta$ AVE	$\Delta$ Sd.
多目标粒子群优化	0.118	2.00E–04	0.047	0.037	1.004	0.845	0.939	0.042
非支配排序遗传算法II	0.118	2.00E–04	0.081	0.012	1.004	0.845	0.939	0.036
MOBSA	0.118	2.00E–04	0.020	0.018	1.004	0.845	0.939	0.042

表5 ZDT6函数的性能优点（GD, $\Delta$）

算法	GD Max	GD Min	GD AVE	GD Sd.	$\Delta$ Max	$\Delta$ Min	$\Delta$ AVE	$\Delta$ Sd.
多目标粒子群优化	0.844	0.001	0.158	0.235	1.325	0.890	1.062	0.120
非支配排序遗传算法II	0.844	0.001	0.486	0.0684	1.325	0.890	1.062	0.031
MOBSA	0.844	0.001	0.042	0.026	1.325	0.890	1.062	0.094

4.3 结果讨论

所有三种算法在基准函数上均进行了200次迭代的仿真。结果在图2、3、4和5中以图形方式展示。每种算法测试了20次，每次分别进行100次迭代。表2、3、4和5显示了使用MOPSO、NSGA‐II和MOBSA三种算法获得的收敛性指标（GD，$\Delta$）的均值和方差。在SCH、ZDT3和ZDT6上，MOBSA得到的GD均值和标准差均小于其他两种算法。对于FON函数，基于MOBSA的GD均值略大于MOPSO，但其标准差在三种算法中最小。为了评估$\Delta$的另一项优点，MOBSA在SCH、FON和ZDT6上的平均值优于其他算法。然而，ZDT3的平均$\Delta$值基于MOPSO取得最优结果。根据这些统计结果，可以得出结论：MOBSA优于MOPSO和NSGA‐II。

5 结论

本文基于非支配排序策略扩展了BSA，以应对无约束的多目标优化问题。对于所提出的名为MOBSA的算法，采用了平行胞坐标系，并使用非支配排序方法和密度评估方法更新外部档案。在不同测试函数上将所提出的MOBSA与MOPSO和NSGA‐II进行了比较。结果证明，MOBSA在大多数测试函数上能够获得更好的解的分布性和收敛性。未来的工作重点是利用MOBSA处理约束多目标优化问题及其在工程问题中的应用。