启发式算法求解混合整数线性优化问题—— 生产计划安排和资源分配

问题描述和范围限定：

生产计划安排分为两种：静态和动态计划。

静态计划生成的时间距离实际生产时间较长，以假设所有预设条件都满足为前提，在给定优化目标下（比如最小延迟，最低库存金额，etc.）寻找最优计划。静态计划一般采用优化算法实现。

动态计划基于静态计划，是在实际排产出现异常时（比如原材料供应不足，设备突然故障造成停线，上游产品突发质量问题，产线工人罢工，etc.）

这篇文章主要关注生成静态计划的优化算法，包括启发式算法和确切算法。更多动态计划的算法有机会再介绍。

这篇文章的优化算法适用于此类计划问题 1). 任务有截止日期，2). 资源为有限资源并且不可持续（比如设备利用率，不可持续性表现在剩余资源有实效且不可存储，过期无效），3).多资源多任务排产，4）任务目标为以最小库存成本在截止日期前完成生产。

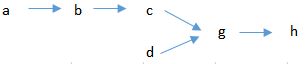
各个任务间可以有层级关系，下游任务可以由多个上游任务合并形成，但是每个上游任务只能对应唯一的下游任务（树形产品结构，成品在根节点，原材料在叶节点，半成品在其他中间节点）。

以测试数据的产品结构为例：a和d为原材料，b,c,g为半成品，h为成品。其中g为assembly。在测试数据中，每个任务有唯一编码。

使用的算法：

Branch and Bound：常用的解决混合整数问题（MIP）的确切算法

确切算法（exact）指能保证找到最优解的一类算法（相对于启发式算法heuristic），在解决问题时往往由于需要搜索庞大的解空间而造成运算量过大运算时间过长。仍然有一些确切算法适合用于求解某一类特定问题，在问题规模可控的条件下能在可接受的时间内给出最优解。

Branch and Bound是一类经常用于求解MIP的确切算法，通过构造树形解空间并以边界形式对解空间剪枝达到有效搜索最优解的目的。在我们的生产日程安排问题中，branch and bound 以非最优有效解作为上边界，松弛问题的最优解（无效解）作为下边界，通过分枝和节点选择规则，将边界解不断分解为子问题分别求解，直到找到最优解。由于存在上下边界，大部分中间节点会因为超过已存在的有效解范围而被剪枝，从而快速缩小解空间，提高算法效率。

详细说明参考百度百科“分枝界限法”条目。

图片来源

Branch and bound算法的核心是如何得到每个节点上的上下边界。常用的方法是Lagrangian relaxation.

Lagrangian Relaxation：常用的线性优化问题降低求解难度的技术

一些由实际场景建模得到的线性优化问题由于存在大量约束条件，使精确求解此类方程组难度增大。Lagrangian relaxation是一类即能保留目标函数线性特点，又能将较难限制条件转化为目标函数一部分的常用松弛方法。此类松弛方程的解可以无限接近于原始方程组的解，因此常常作为原始解的限制边界，应用于组合优化算法中。

比如在我们的生产日程安排问题中，将使用Lagrangian relaxation方法得到节点的下边界，并在此基础上使用启发式算法（Lagrangian heuristic），得到有效的然而可能非最优的解作为节点上边界。

简单来说，假设原始问题为

P: minimize $c^{T}x$

subject to:

$Ax\ge b$ (假设为难约束)，$Bx\le d$ （假设为简单约束），$x\in {\mathbb{Z}}_{+}^n$

可以转化为求解松弛问题

PL: minimize $c^{T}x+{\lambda }^T(b-Ax)$

s.t. $Bx\le d$，$x\in {\mathbb{Z}}_{+}^n$

详细说明参考百度百科“拉格朗日松弛技术”条目

其中 $ \lambda $是Lagrangian multiplier（拉格朗日乘数）。对于Lagrangian multiplier的取值，一般采用subgradient方法迭代求解。

Subgradient：不可导函数的梯度法求极值

梯度法是常用的求解方程的方法。在给定目标下，首先随机选取一组方程的初始（无效）解，根据计算目标值和实际目标值的差异判断下一次迭代中尝试的解应该向哪个方向调整。梯度可以标识调整方向，是通过对损失函数求一阶导得到的。

然而在优化问题中，由于有限制条件的存在，损失函数往往不可导。所以不能采用梯度法，而是使用很相似的次梯度法标识每次迭代解的调整方向。

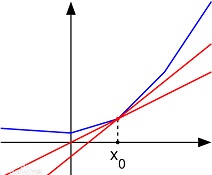
详细说明参考百度百科“次导数”条目

案例：工厂生产计划安排

测试数据：

假设产品结构如上图。

a, d为独立原材料，b,c,g为生产过程中的半成品，h为成品。

作为测试数据，假设需要生产4件相同产品，唯一编号分别为任务名+1-4，产品结构以“上游任务”和“下游任务”两个字段连接，其中“下游任务”只可能有一个产品编号；“上游任务”可以有多个编号，代表装配任务。执行任务的设备分别为mk11-16，上游设备编号不能小于下游设备编号（启发式算法将从最下游设备开始排产）。其他如运行时间，库存成本，订单截止日期 etc.如下表所示：

任务	设备	上游任务	下游任务	运行时长	成品编号	截止日期	单位时间库存成本
a1	mk16		b1	3	h1	50	1
b1	mk15	a1	c1	2	h1	50	2
c1	mk14	b1	g1	5	h1	50	4
d1	mk13		g1	4	h1	50	1
g1	mk12	c1, d1	h1	6	h1	50	8
h1	mk11	g1		1	h1	50	10
a2	mk16		b2	3	h2	60	1
b2	mk15	a2	c2	2	h2	60	2
c2	mk14	b2	g2	5	h2	60	4
d2	mk13		g2	4	h2	60	1
g2	mk12	c2, d2	h2	6	h2	60	8
h2	mk11	g2		1	h2	60	10
a3	mk16		b3	3	h3	65	1
b3	mk15	a3	c3	2	h3	65	2
c3	mk14	b3	g3	5	h3	65	4
d3	mk13		g3	4	h3	65	1
g3	mk12	c3, d3	h3	6	h3	65	8
h3	mk11	g3		1	h3	65	10
a4	mk16		b4	3	h4	70	1
b4	mk15	a4	c4	2	h4	70	2
c4	mk14	b4	g4	5	h4	70	4
d4	mk13		g4	4	h4	70	1
g4	mk12	c4, d4	h4	6	h4	70	8
h4	mk11	g4		1	h4	70	10

建模构造原始问题：

i: 当前任务编号

k: 当前设备编号

$\varphi (i)$: 当前任务的紧邻下游任务集（immediate successors）

$\phi (i)$: 当前任务对应的最终成品编号

$\Lambda (i)$: 当前任务的紧邻上游任务集（immediate predecessors）

Mk: 将在当前设备上排产的任务集

F: 成品集

$p_i$: 任务 i 的运行时长

$d_i$: 任务 i 的成品截止时间

$h_i$: 任务 i 的每件每单位时间库存成本

L: 一个足够大的正值

求解任务sequence和开始时间：

$s_i$: 任务 i 的开始时间

$y_{ij}$: 0/1，如果为1则代表 i 在 j 前发生

原始日程安排问题为：

$(\mathrm{P}):\text{minimize }z={\sum }_{i\notin F}{h}_i(s_{\varphi (i)}-s_i)+{\sum }_{i\in F}{h}_i(d_i-s_i)$

s.t.

$s_i+p_i-s_j\le L\cdot (1-y_{ij})\text{ for }i,j\in M_k(i<j)\text{ and }\forall k$, (2)

$s_j+p_j-s_i\le L\cdot y_{ij}\text{ for }i,j\in M_k(i<j)\text{ and }\forall k$, (3)

$s_i+p_i\le d_i,\text{for }i\in F$, (4)

$s_i+p_i\le s_{\varphi (i)},\text{for }i\notin F$, (5)

$s_i\ge 0,\forall i$, (6)

$y_{ij}=0,1\text{ for }i,j\notin M_k(i<j)\text{ and }\forall k$. (7)

通过定义阶梯库存成本echelon inventory，可以进一步简化原始问题 § 为：

$(\mathrm{P}):\text{minimize }z={\sum }_i{e}_i(d_{\phi (i)}-s_i)$, (8)

其中：

$e_i\equiv h_i-{\sum }_{j\in \Lambda (i)}{h}_j,\forall i$,

$d_{\phi (i)}$ 是 i 对应成品的截止时间。

建模和算法实现基于这篇论文。

将原始问题转化为松弛问题，并拆解为独立的单设备多任务排产松弛问题，分别求解：

通过松弛(4), (5)两项限制，可以得到新的松弛问题：

( L R λ ) :  minimize  ∑ ∀ i ( λ i − e i − ∑ j ∈ Λ ( i ) λ j ) s i + ∑ ∀ i ( e i d φ ( i ) + λ i p i ) − ∑ i ∈ F λ i d i (\mathrm{LR}_\lambda): \text{ minimize } \sum_{\forall i} \big( \lambda_i - e_i - \sum_{j \in \Lambda(i)} \lambda_j \big) s_i + \sum_{\forall i} \big( e_i d_{\varphi(i)} + \lambda_i p_i \big) - \sum_{i \in F} \lambda_i d_i (LRλ​): minimize ∑∀i​(λ