基于模糊逻辑的智能家居节能管理

基于模糊逻辑的智能家居用户侧管理方法研究

摘要

智能电网环境要求用户积极参与节能，并将负载转移到非高峰时段，以平衡电源与负载之间的电力。在这种情况下，由于手动调整家用电器运行的难度较大，用户的偏好、自我调节和自我调度受到越来越多的关注。需要一种自主调度器，使家用电器能够自动运行，以节约成本和能源，同时不降低用户的舒适度。本文提出了一种基于模糊逻辑的智能方法，通过将电力需求转移至非高峰时段，为用户提供建议。所提出的基于模糊逻辑规则的方法包括时间片、投标成本、功率额定值、单个负载每日总运行时长、负载的优选和非优选时间段作为输入，负载的开关状态作为输出。在此，家用电器被分为基本负载和可调度负载。用户舒适度、成本和需求响应是设计基于模糊逻辑的负荷管理调度器所考虑的三个优化变量。仿真结果表明，该系统在考虑用户舒适度和重新调度的情况下，能够支持用户对可控负荷管理的决策，实现可能的经济效益。

关键词 ：需求响应，模糊逻辑，智能电网

一. 引言

智能电网技术的应用之一是智能家居，它可以提供多种节能方式。这有助于同时减少温室气体排放和能源使用。智能家居不仅节省电能，还能带来诸多好处，例如提高稳定性、舒适度、增强家庭自动化以及对电力的控制。[1]

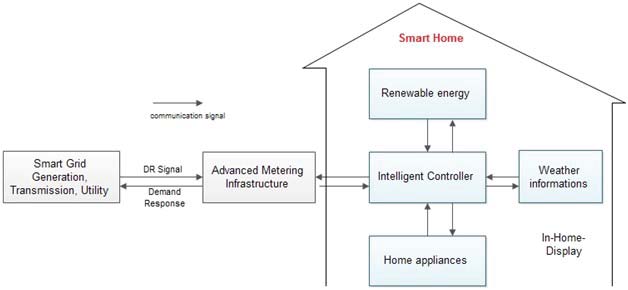
图1展示了具有需求响应（DR）信号的智能家居架构。智能控制器向家用电器和可再生能源发送/接收信号。天气状况也与智能控制器相连，以维持用户的舒适度。需求响应信号通过高级计量基础设施（AMI）从公用事业公司接收。

需求响应（DR）是一种用户侧管理机制，其中电力的终端用户通过改变其正常的能源消费模式，鼓励终端用户参与降低系统的峰值负荷。作为回报，终端用户将获得价格或服务激励。最终，随着终端用户将部分负载从峰值时段或高电价时段转移至非峰值时段或低电价时段，这一过程有望降低整个系统的峰值负荷。[2]

参与需求响应对用户和能源生产者都有重大好处，即帮助用户节省高昂的电力成本，并使公用事业公司能够降低峰值负荷。需求响应策略旨在减轻能源供应商的压力，并降低用户的能源成本。为了维持平衡状态，有必要采用基于智能或优化技术的需求侧负荷管理系统。通过调节居民负荷，需求侧管理能够快速应对供需失离。一旦提供需求响应所需的信息和基础设施，用户便可应用需求侧负荷管理算法来实施需求侧管理策略。

许多智能技术的突破推动了智能家居能源管理系统（HEMS）与住宅内多种功能的集成，例如自动监控、智能电表和较低能耗。由于全球变暖和能源短缺问题日益受到关注，智能家居的重要性日益凸显。实际上，它有助于在用电高峰期减少电力需求[3]。与智能家居相关的各种组件包括智能电表、能源管理系统、能量存储、智能电器和分布式发电。文献[4]对巴西实施的智能电网试点项目的优缺点进行了深入研究，同时讨论了主动需求侧管理（ADSM）、智能输电、配电和发电。用户可根据能源供应商发布的需求响应信号[5]来控制家用电器。作者仅提出了构想，未进行实时实现。

一种基于规则的家庭能源管理算法在实验室中被开发并集成到负载控制器中[6]。该研究说明了通过设定用户偏好可以减少多少功率。负载将根据设计的算法进行启动，而非依据实时电价。借助机器学习算法和传感技术，开发了一种基于硬件的家庭能源管理系统（HEMS）原型，以最小化能源成本并智能地控制负载[7]。该硬件架构通过无线网络调节温控设定点来实现空调单元的开启与关闭，未考虑实时能源成本[8]。在布加勒斯特理工大学的实验室中，使用树莓派开发了一个基于硬件的智能家居模拟器，能够响应供应商信号[9]。

在[10]中展示了基于预设优先级的家用电器家庭能源管理。优先级根据使用情况固定，而不依据时间段和实时电价。为了降低能耗成本，提出了一种家庭能源管理调度器，该调度器在三个不同阶段运行，即实时监控、随机调度和实时控制[11]。在计算总能耗成本以及选择一组家庭控制设备时，采用了随机动态规划。最后，通过实时监控实时显示家庭的可控负载。然而，所实现的智能算法较为复杂，具有较高的计算负载和较低的运行速度。

利用定制软件开发了家庭能源管理，以实现家用电器的开关状态控制和监控[12]。该开发系统的目的是提高对用电情况的认知。该软件兼容Linux，使用Java、Python和HTML编写。

智能电网技术的主要特征之一是可再生能源集成[13]。在[14]中，开发了集成了光伏和储能资源的智能家居。通过安装光伏系统和电池来满足智能家居的能源需求。用电管理系统由自学习反馈机制进行维护。光伏系统将与家用电器交互以维持舒适度。

已采用多种人工智能策略来开发家用电器调度器。人工智能（AI）利用计算机编程来模拟和理解人类智能[15‐17]。人工神经网络是人工智能的一个分支，是一种信息处理系统，有助于模拟非线性系统并模仿人脑[18]。模糊逻辑控制器易于执行，能够处理基于语言的线性和非线性系统，且无需数学模型[18]。

观察到模糊逻辑系统在解决需求侧管理（DSM）问题时更为合适且简单，因此所提出的系统采用了模糊逻辑控制器。本文开发了一种基于简单高效模糊逻辑控制器的需求侧管理方法，能够在适当的时间操作负载，同时不牺牲用户的舒适度。本文其余部分安排如下：在引言之后，介绍了模糊逻辑控制的综述；第3节阐述了所提出的需求响应方法，第4节详细说明了所提出的用于需求响应的模糊逻辑控制器（FLC）的开发过程；第5节提供了仿真细节；最后，第6节对全文进行了总结。

II. 模糊逻辑综述

模糊逻辑源自模糊集的推理理论，这种推理是近似的，而不是从经典谓词逻辑中精确推导出来的。模糊集理论提供了一种表达系统中由于模糊性或无法解释的行为所导致的模糊性的优秀方法。这可以反映人工控制的过程，也能够使实验知识改变控制器参数。所有实值输入数据首先通过静态定义的隶属函数进行模糊化。隶属度函数为模糊集域中的每个点分配一个0到1之间的值。首先，模糊逻辑控制的核心思想是用自然语言描述输入参数，并定义不同参数之间的关系。

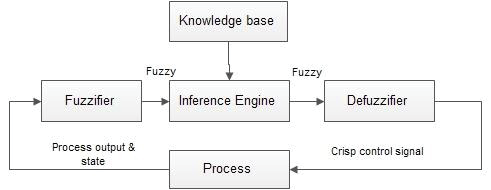
借助模糊规则集对输入和输出进行处理。通过一组规则来组合输入和输出集，以获得输入状态对应的输出。因此，模糊系统遵循的各个步骤包括：输入变量的模糊化、规则评估、规则输出聚合以及去模糊化，如图2[19]所示。在图2中，规则基于外部世界知识构建，并且也规定了如何响应输入信号。该系统持续分析可用的输入，并基于规则对系统输出做出决策。

III. 需求响应的提出方法

为解决上述问题，本文采用了一种基于模糊逻辑的住宅建筑需求侧负荷管理新概念。在此方法中，根据成本和需求，通过切断部分负载来限制用电高峰期的电力使用，并将这些负载转移到其他时段，特别是非高峰时段。所提出的CSM是利用模糊逻辑工具箱设计的。模糊系统遵循的各个步骤包括输入变量的模糊化、规则形成、规则输出聚合以及去模糊化，如图2所示。此处制定的规则基于外部世界知识，规定了输入信号如何响应变化。该系统持续分析可用输入，并依据规则确定系统输出。

严格来说，58条规则是基于如果‐那么规则构建的，并作为模糊逻辑控制器（FLC）的知识库。采用了马丹尼提出的非常流行的语言学方法，因其在设计模糊逻辑控制器时复杂度较低。这些规则由五个输入参数和两个输出参数构成。输入参数包括24小时内的负荷需求时间段、通过智能计量架构获得的实时电价（RTP）、家用电器的功率等级、电器运行时长以及家用电器的首选运行时间。本文所考虑的家用电器包括洗衣机、电机、研磨机和电熨斗。输出参数为家用电器的开关状态。时间段被划分为0到24小时，投标成本根据预录投标值限制在ē.0到ē2之间。功率等级根据家用电器的使用情况被划分为100瓦到2000瓦。输出参数为开和关状态，分别用0和1表示。

在表1中，描述了家用电器开启的优选条件。根据用户负载的使用情况，24小时被划分为极低峰时段、低峰时段、高峰期和关键高峰期。根据时段的划分，实时定价被确定为非常低、低、中、高和非常高。

每个负载的功率额定值被标记为低、中和高瓦数等级。每个负载的营业时间被分为低、中和高。每个负载的优选运行时间段基于用户舒适度进行分类。

时间槽	投标成本 (ē)	功率评分 (瓦特)	运行小时数 (小时)	优选/非优选时间	电器 (开启/关闭)
Very low 高峰期 24.00‐06.00	ē 0‐ē 0.25 Very low	100-500W Low	0‐1/2小时 Low	早晨 10.00‐12.00 下午 14.00‐16.00 晚上 19.00‐21.00	洗衣机 ON-1 关闭‐0
高峰期 06.00‐12.00	ē 0.25‐ē 0.50 Low	500-1000瓦 中 m	1/2–1 Hr. 中	早晨 6.00‐8.00 晚上 17.00‐19.00	电机 ON-1 关闭‐0
Low Peak time 12.00‐17.00	ē 0.50‐ē 1 中 m	1000瓦-1500瓦 High	1‐2小时 High	早晨 09.00‐10.00 晚上 16.00‐17.00 夜晚 18‐19.00	研磨机 ON-1 关闭‐0
关键峰值 time 17.00‐23.00	ē 1‐ē 1.50 High	1000瓦-1500瓦 High		早晨 08.00‐09.00 After 下午。15.00‐16.00 夜晚 21.00‐22.00	电熨斗 ON-1 关闭‐0
关键峰值 time 17.00‐23.00	≥ē 1.50 Very high	1000瓦-1500瓦 High		早晨 08.00‐09.00 After 下午。15.00‐16.00 夜晚 21.00‐22.00	电熨斗 ON-1 关闭‐0

持续时间

IV. 用于需求响应的模糊逻辑控制器开发

为了设计模糊逻辑控制器，需要正确确定以下决策。
- 模糊逻辑控制器的输入和输出选择
- 隶属度函数
- 模糊规则库构建。

4.1. 系统设计和输入‐输出参数

所建议的模糊逻辑控制器具有五个输入：它们是时间片、投标价格、单个负载的每日功率额定值、总运行小时数以及优选和非优选负载时间段。两个输出为负载的开关状态。图3描述了模糊逻辑控制器的示意图。

本研究提出了一种基于模糊逻辑控制器的需求侧管理系统。在所提出的策略中，包含四种不同的家用电器（可调度负载）考虑了不同的耗电能力和允许运行时段。一天24小时被划分为四个时隙：极低峰、低峰时段、高峰期和关键高峰期。表1显示了模糊逻辑控制器的输入和输出分类。用户舒适度、成本和需求响应是设计基于模糊逻辑的负荷管理调度器时考虑的三个优化变量。预设优先级基于用户行为确定。

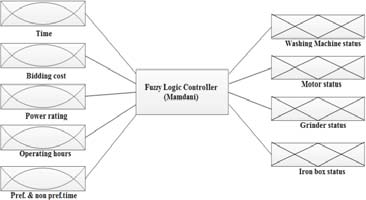
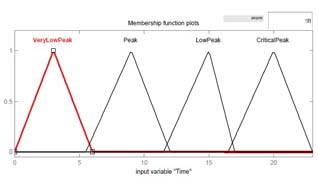
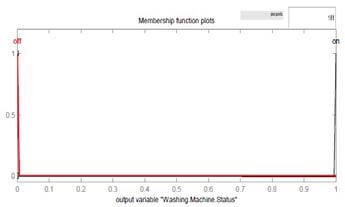
图4展示了模糊输入和输出变量的示意图。由于该系统的目标是自动参与需求响应以节约能源和进行负载管理，因此假设在现有的智能电表中嵌入了模糊逻辑概念。图4a至图4f表示使用模糊工具箱开发的输入和输出隶属度函数图。

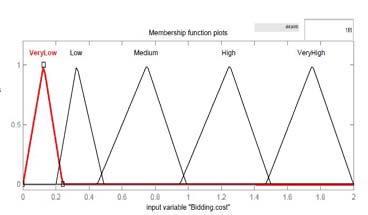
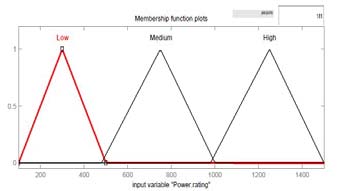
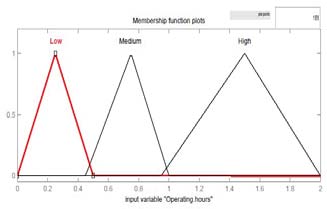
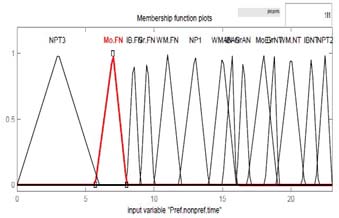
V. 结果与讨论

为了分析所提出的DSM的性能，该结构由MATLAB Simulink工具箱开发。在此，FLC的输入参数通过常量节点获得，这些节点通过多路复用器连接到FLC。多路分解器用于分离输出，其中连接LED灯以显示结果。在本提出的工作中，考虑了若干案例以验证所开发的DSM模型，部分案例的详细信息如下。

案例1(a)：高峰期洗衣机的状态

洗衣机的优选运行时间为早晨：10.00–12.00，下午：14.00–16.00，晚上：19.00–21.00。在情况1中，选取两个优选时间11.00和14.00进行验证。

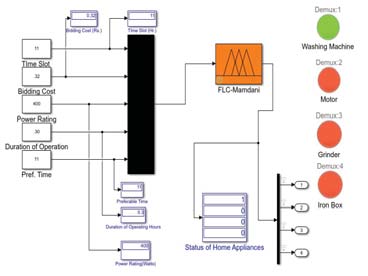
在上述Simulink模型图5a中，所选时隙为上午11点，接收到的该时段实时电价为ē 0.32，其值在ē 0.25至0.5之间变化。由于所选负载的功率额定值为400瓦，首选运行时间为30分钟，因此洗衣机处于开启状态，其余负载处于关闭状态。

案例1(b)：低峰时段洗衣机的状态

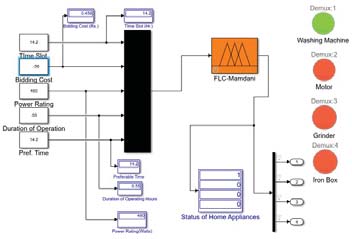
在上述Simulink模型图5b中，所选时隙为14.2，该时段接收到的实时电价为ē 0.56，其值在ē 0.5到1之间变化。由于所选负载的功率额定值为480瓦，首选运行时间约为55分钟，因此洗衣机处于开启状态，其余负载处于关闭状态。

案例2：电机状态

电机的优选运行时间为早晨：06.00–08.00，以及晚上：17.00–19.00。在案例2中，考虑了一个优选时段进行验证。

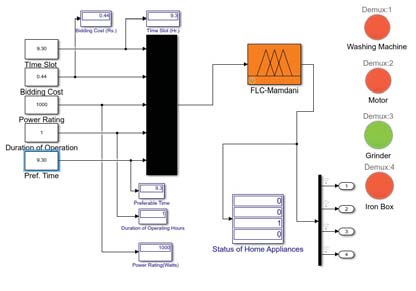
图6显示了电机开启状态的Simulink模型。在上述Simulink模型中，优选的时隙为7.00上午，对应时隙的实时电价为ē0.30。用户优先使用500瓦至1000瓦范围内的负载，此处选择400瓦，这些负载的营业时间需运行约30分钟至1小时，因此在可用负载中开启电机，其余负载处于关闭状态。

案例3：研磨机状态

研磨机的操作时段为：早晨：09.00–10.00，晚上：16.00–17.00，夜晚：18:00–19:00。在三个时隙中，选取09.00–10.00用于验证。

图7显示了研磨机开启状态的Simulink模型。在上述Simulink模型中，首选时隙为上午9:30，该时隙接收到的实时电价为0.44卢比。用户优先使用1000瓦至1500瓦范围内的负载，此处选择1000瓦，这些负载的营业时间约为1小时。在此状态下，研磨机在可用负载中处于开启状态，其余负载则处于关闭状态。

根据上述分析可知，所提出的模型能够建议用户在不降低舒适度的情况下，在实时电价较低时运行其负载。

VI. 结论

在本研究中，提出了一种模糊逻辑方法，以促进能源账单与其暖通空调系统密切相关的用户参与需求响应。开发了基于模糊的需量侧管理，运行需量侧管理所需的数据来自智能电表。该需量侧管理在Simulink中设计，并通过四种不同家用电器的四个案例进行了验证。所开发的CSM用于向用户提供信息，以实现低成本运行负载的目标。基于模糊逻辑控制器的需量侧管理在不同场景下表现良好。结果表明，由于模糊方法提供的建议，与现有方法相比，该方法显著分散了住宅建筑中的能源使用。此外，该系统能够在无需用户干预的情况下自动参与需求响应。