std::sort源码剖析

最新推荐文章于 2024-11-15 10:53:19 发布

原创

最新推荐文章于 2024-11-15 10:53:19 发布 · 1.2k 阅读

3 ·

CC 4.0 BY-SA版权

本文深入剖析了C++标准库中的std::sort算法，揭示了其结合快速排序、插入排序和堆排序的混合设计，以实现高效排序。在数据量较大时，std::sort采用快速排序，分段较小则转为插入排序，当递归过深或分割恶化时，利用堆排序。文章详细分析了算法的递归结构、中值选择、分割策略以及递归深度和分段阈值的设定，同时探讨了不同插入排序算法的性能差异和实现细节。通过对std::sort源码的解读，展示了其在效率和优化方面的精妙之处。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章参考：源码

这篇文章在一个偶然的机会看到，我原先也是知道sort函数效率高，但终究没有去了解原因，读了这篇文章更加钦佩C++大师积年累月智慧的结晶和对效率的极致追求，看到很多地方不禁暗暗称奇。也还是感慨原文作者对技术的追求和细致的讲解，下面的内容大多来自作者的文章，其中加入了自己的理解，也不枉费大半个下午的时间。

从事程序设计行业的朋友一定对排序不陌生，它从我们刚刚接触数据结构课程开始便伴随我们左右，是需要掌握的重要技能。任何一本数据结构的教科书一定会介绍各种各样的排序算法，比如最简单的冒泡排序、插入排序、希尔排序、堆排序等。在现已知的所有排序算法之中，快速排序名如其名，以快速著称，它的平均时间复杂度可以达到O(NlogN)，是最快排序算法之一。

背景

在校期间，为了掌握这些排序算法，我们不得不经常手动实现它们，以加深对其的理解。然而这些算法实在是太常用了，我们不太可能在每次需要时都手动来实现，不管是性能还是安全性都得不到保证。因此这些算法被包含进了很多语言的标准库里，在C语言的标准库中，stdlib.h头文件就有sort算法，它正是最快排序算法——快速排序的标准实现，这给我们提供了很大的方便。

然而，快速排序虽然平均复杂度为O(N logN)，却可能由于不当的pivot选择，导致其在最坏情况下复杂度恶化为O(N2)。另外，由于快速排序一般是用递归实现，我们知道递归是一种函数调用，它会有一些额外的开销，比如返回指针、参数压栈、出栈等，在分段很小的情况下，过度的递归会带来过大的额外负荷，从而拉缓排序的速度。

Introspective Sort

为了解决快速排序在最坏情况下复杂度恶化的问题，人们进行了大量的研究，获得了众多研究成果。本文将要介绍的算法便是其中之一。在开始之前我们需要先简短介绍两个其它常用的算法，这对我们理解新算法为何如此设计非常重要，它们是堆排序和插入排序。

堆排序经常是作为快速排序最有力的竞争者出现，它们的复杂度都是O(N logN)。这里有一个维基百科上的动态图片，直观的反应出堆排序的过程：

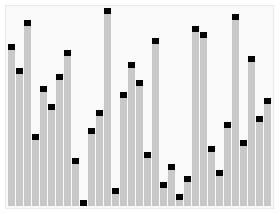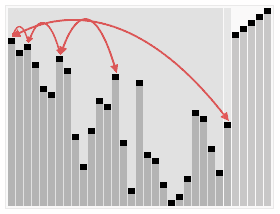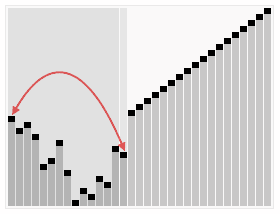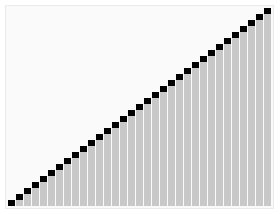
虽然两者拥有一样的复杂度，但就平均表现而言，它却比快速排序慢了2~5倍，知乎上有一个讨论：堆排序缺点何在？
但是，有一点它却比快速排序要好很多：最坏情况它的复杂度仍然会保持O(N logN)这一优点对本文介绍的新算法有着巨大的作用。

插入排序的优点

再来看看插入排序，同样有一张维基百科上的动态图片，可以唤起你对它的记忆：

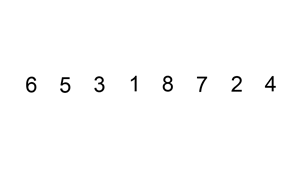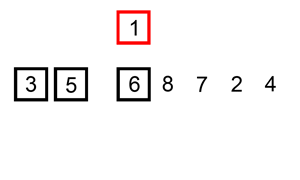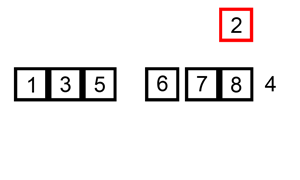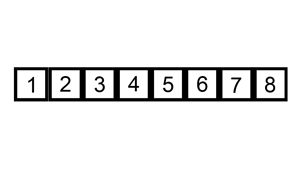
它在数据大致有序的情况表现非常好，可以达到O(N)，可以参考这个讨论Which sort algorithm works best on mostly sorted data? 这一优点也被新算法所采用。

横空出世

到了正式介绍新算法的时刻。由于快速排序有着前面所描述的问题，因此Musser在1996年发表了一遍论文，提出了Introspective Sorting(内省式排序)，这里可以找到PDF版本。它是一种混合式的排序算法，集成了前面提到的三种算法各自的优点：

在数据量很大时采用正常的快速排序，此时效率为O(logN)。
一旦分段后的数据量小于某个阈值，就改用插入排序，因为此时这个分段是基本有序的，这时效率可达O(N)。
在递归过程中，如果递归层次过深，分割行为有恶化倾向时，它能够自动侦测出来，使用堆排序来处理，在此情况下，使其效率维持在堆排序的O(N logN)，但这又比一开始使用堆排序好。

由此可知，它乃综合各家之长的算法。也正因为如此，C++的标准库就用其作为std::sort的标准实现。

std::sort的实现

SGI版本的STL一直是评价最高的一个STL实现，在技术层次、源代码组织、源代码可读性上，均有卓越表现。所以它被纳为GNU C++标准程序库。这里选择了侯捷的《STL源码剖析》一书中分析的GNU C++ 2.91版本来作分析，此版本稳定且可读性强。

std::sort的代码如下：

 template <class RandomAccessIterator>
 inline void sort(RandomAccessIterator first, RandomAccessIterator last) {
     if (first != last) {
         __introsort_loop(first, last, value_type(first), __lg(last - first) * 2);
         __final_insertion_sort(first, last);
     }
 }

它是一个模板函数，只接受随机访问迭代器。if语句先判断区间有效性，接着调用__introsort_loop，它就是STL的Introspective Sort实现。在该函数结束之后，最后调用插入排序。我们来揭开该算法的面纱：

 template <class RandomAccessIterator, class T, class Size>
  void __introsort_loop(RandomAccessIterator first,
                        RandomAccessIterator last, T*,
                        Size depth_limit) {
      while (last - first > __stl_threshold) {
          if (depth_limit == 0) {
              partial_sort(first, last, last);
              return;
          }
         --depth_limit;
         RandomAccessIterator cut = __unguarded_partition
           (first, last, T(__median(*first, *(first + (last - first)/2),
                                    *(last - 1))));
         __introsort_loop(cut, last, value_type(first), depth_limit);
         last = cut;
     }
 }

这是算法主体部分，代码虽然不长，但充满技巧，有很多细节需要注意，接下来我们将对其一一展开分析。

递归结构

可以看出它是一个递归函数，因为我们说过，Introspective Sort在数据量很大的时候采用的是正常的快速排序，因此除了处理恶化情况以外，它的结构应该和快速排序一致。但仔细看以上代码，先不管循环条件和if语句(它们便是处理恶化情况所用)，循环的后半部分是用来递归调用快速排序。但它与我们平常写的快速排序有一些不同，对比来看，以下是我们平常所写的快速排序的伪代码：

function quicksort(array, left, right)
      // If the list has 2 or more items
      if left < right
          // See "#Choice of pivot" section below for possible choices
          choose any pivotIndex such that left ≤ pivotIndex ≤ right
          // Get lists of bigger and smaller items and final position of pivot