通过上一篇文章六自由度机器人正解已经获得了机器人各连杆间的转换关系。当知道各个连杆的转角1、
2、
3、
4、
5、
6时可以求出末端执行器的位姿,这个过程称为正向运动学。这篇文章将讨论逆向运动学,即,给定末端执行器的位姿,求解各连杆的转角。在实际生活中逆向运动学更为实用。
现已知末端姿态矩阵和机器人的运动学模型,求解1、
2、
3、
4、
5、
6。
已知六轴机器人的D-H参数如下所示:
如果不清楚何为改进的DH参数,可以看我的上一篇博客。【机器人学】1-1.六自由度机器人运动学正解 【附MATLAB代码】
| 关节1 | 关节2 | 关节3 | 关节4 | 关节5 | 关节6 | |
| 0 | 90 | 0 | 0 | -90 | 90 | |
| a | 0 | 0 | 425 | 393 | 0 | 0 |
| d | 160.7 | 0 | 0 | 113.3 | 99 | 93.6 |
| 0 | 90 | 0 | -90 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 |
选用改进型的D-H参数,各矩阵分别如下所示:

设

其中






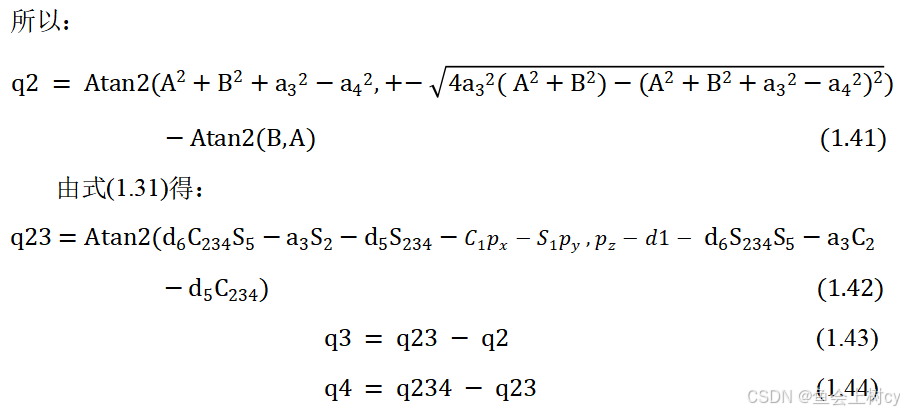


如果你的机械臂D-H参数结构和我的一致,以上解析解你可以直接使用,如果参数相差不大,可以跟着我的计算思路推导一下你自己的逆解方程,相信你也可以得到正确的结果。
MATLAB仿真验证
function R=AxisAngle_RotMat(Rxyz)
theta=(Rxyz(1)^2+Rxyz(2)^2+Rxyz(3)^2)^0.5;
if(abs(theta)<1e-8)
R=eye(3);
return;
end
r=Rxyz/theta;
R=[r(1)^2*(1-cos(theta))+cos(theta) r(1)*r(2)*(1-cos(theta))-r(3)*sin(theta) r(1)*r(3)*(1-cos(theta))+r(2)*sin(theta)
r(1)*r(2)*(1-cos(theta))+r(3)*sin(theta) r(2)^2*(1-cos(theta))+cos(theta) r(2)*r(3)*(1-cos(theta))-r(1)*sin(theta)
r(1)*r(3)*(1-cos(theta))-r(2)*sin(theta) r(2)*r(3)*(1-cos(theta))+r(1)*sin(theta) r(3)^2*(1-cos(theta))+cos(theta)];
endclc;clear;
%带入机器人初始值
d1 = 0.1607;
d2 = 0;
d3 = 0;
d4 = 0.1133;
d5 = 0.099;
d6 = 0.0936;
a1 = 0;
a2 = 0;
a3 = 0.425;
a4 = 0.393;
a5 = 0;
a6 = 0;
%testData1 测试数据
px = 0.129;
py = 0.157;
pz = 0.858;
rx = 38.05;
ry = 42.96;
rz = -179.77;
posture = [rx/180*pi,ry/180*pi,rz/180*pi];
%轴线表示转换为姿态矩阵转
a = AxisAngle_RotMat(posture);
%目标位置姿态矩阵
nx=a(1,1);ox=a(1,2);ax=a(1,3);
ny=a(2,1);oy=a(2,2);ay=a(2,3);
nz=a(3,1);oz=a(3,2);az=a(3,3);
% 求解关节角1
t1 = (d6*a(1,3)-px);
t2 = (d6*a(2,3)-py);
theta1_1 = atan2(t2,t1) - atan2(d4, sqrt(t1^2+t2^2-d4^2)) ;
theta1_2 = atan2(t2,t1) - atan2(d4, -sqrt(t1^2+t2^2-d4^2)) ;
disp([theta1_1 theta1_2]*180/pi);
% 求解关节角5
theta5_1 = atan2(sqrt((ny*cos(theta1_1)-nx*sin(theta1_1))^2+(oy*cos(theta1_1)-ox*sin(theta1_1))^2), ax*sin(theta1_1)-ay*cos(theta1_1));
theta5_2 = atan2(-sqrt((ny*cos(theta1_1)-nx*sin(theta1_1))^2+(oy*cos(theta1_1)-ox*sin(theta1_1))^2), ax*sin(theta1_1)-ay*cos(theta1_1));
theta5_3 = atan2(sqrt((ny*cos(theta1_2)-nx*sin(theta1_2))^2+(oy*cos(theta1_2)-ox*sin(theta1_2))^2), ax*sin(theta1_2)-ay*cos(theta1_2));
theta5_4 = atan2(-sqrt((ny*cos(theta1_2)-nx*sin(theta1_2))^2+(oy*cos(theta1_2)-ox*sin(theta1_2))^2), ax*sin(theta1_2)-ay*cos(theta1_2));
disp([theta5_1 theta5_2 theta5_3 theta5_4]*180/pi);
% 求解关节角6
theta6_1 = atan2((ox*sin(theta1_1)-oy*cos(theta1_1))/sin(theta5_1), -(nx*sin(theta1_1)-ny*cos(theta1_1))/sin(theta5_1));
theta6_2 = atan2((ox*sin(theta1_1)-oy*cos(theta1_1))/sin(theta5_2), -(nx*sin(theta1_1)-ny*cos(theta1_1))/sin(theta5_2));
theta6_3 = atan2((ox*sin(theta1_2)-oy*cos(theta1_2))/sin(theta5_3), -(nx*sin(theta1_2)-ny*cos(theta1_2))/sin(theta5_3));
theta6_4 = atan2((ox*sin(theta1_2)-oy*cos(theta1_2))/sin(theta5_4), -(nx*sin(theta1_2)-ny*cos(theta1_2))/sin(theta5_4));
disp([theta6_1 theta6_2 theta6_3 theta6_4]*180/pi);
% 求解关节角2,3,4
q234_1 = atan2(az/sin(theta5_1), (ax*cos(theta1_1)+ay*sin(theta1_1))/sin(theta5_1));
q234_2 = atan2(az/sin(theta5_2), (ax*cos(theta1_1)+ay*sin(theta1_1))/sin(theta5_2));
q234_3 = atan2(az/sin(theta5_3), (ax*cos(theta1_2)+ay*sin(theta1_2))/sin(theta5_3));
q234_4 = atan2(az/sin(theta5_4), (ax*cos(theta1_2)+ay*sin(theta1_2))/sin(theta5_4));
disp([q234_1 q234_2 q234_3 q234_4]*180/pi);
A_1 = d6*sin(theta5_1)*cos(q234_1)-d5*sin(q234_1)-px*cos(theta1_1)-py*sin(theta1_1);
B_1 = pz-d1-d5*cos(q234_1)-d6*sin(theta5_1)*sin(q234_1);
A_2 = -px*cos(theta1_1)-py*sin(theta1_1)-d5*sin(q234_2)+d6*sin(theta5_2)*cos(q234_2);
B_2 = pz-d1-d5*cos(q234_2)-d6*sin(theta5_2)*sin(q234_2);
A_3 = -px*cos(theta1_2)-py*sin(theta1_2)-d5*sin(q234_3)+d6*sin(theta5_3)*cos(q234_3);
B_3 = pz-d1-d5*cos(q234_3)-d6*sin(theta5_3)*sin(q234_3);
A_4 = -px*cos(theta1_2)-py*sin(theta1_2)-d5*sin(q234_4)+d6*sin(theta5_4)*cos(q234_4);
B_4 = pz-d1-d5*cos(q234_4)-d6*sin(theta5_4)*sin(q234_4);
% 关节2
theta2_1 = atan2(A_1^2+B_1^2+a3^2-a4^2, sqrt(abs(4*a3^2*(A_1^2+B_1^2)-(A_1^2+B_1^2+a3^2-a4^2)^2)))-atan2(B_1, A_1);
theta2_2 = atan2(A_1^2+B_1^2+a3^2-a4^2, -sqrt(abs(4*a3^2*(A_1^2+B_1^2)-(A_1^2+B_1^2+a3^2-a4^2)^2)))-atan2(B_1, A_1);
theta2_3 = atan2(A_2^2+B_2^2+a3^2-a4^2, sqrt(abs(4*a3^2*(A_2^2+B_2^2)-(A_2^2+B_2^2+a3^2-a4^2)^2)))-atan2(B_2, A_2);
theta2_4 = atan2(A_2^2+B_2^2+a3^2-a4^2, -sqrt(abs(4*a3^2*(A_2^2+B_2^2)-(A_2^2+B_2^2+a3^2-a4^2)^2)))-atan2(B_2, A_2);
theta2_5 = atan2(A_3^2+B_3^2+a3^2-a4^2, sqrt(abs(4*a3^2*(A_3^2+B_3^2)-(A_3^2+B_3^2+a3^2-a4^2)^2)))-atan2(B_3, A_3);
theta2_6 = atan2(A_3^2+B_3^2+a3^2-a4^2, -sqrt(abs(4*a3^2*(A_3^2+B_3^2)-(A_3^2+B_3^2+a3^2-a4^2)^2)))-atan2(B_3, A_3);
theta2_7 = atan2(A_4^2+B_4^2+a3^2-a4^2, sqrt(abs(4*a3^2*(A_4^2+B_4^2)-(A_4^2+B_4^2+a3^2-a4^2)^2)))-atan2(B_4, A_4);
theta2_8 = atan2(A_4^2+B_4^2+a3^2-a4^2, -sqrt(abs(4*a3^2*(A_4^2+B_4^2)-(A_4^2+B_4^2+a3^2-a4^2)^2)))-atan2(B_4, A_4);
disp([theta2_1 theta2_2 theta2_3 theta2_4 theta2_5 theta2_6 theta2_7 theta2_8]*180/pi);
q23_1 = atan2(-px*cos(theta1_1)-py*sin(theta1_1)-d5*sin(q234_1)+d6*sin(theta5_1)*cos(q234_1)-a3*sin(theta2_1),pz-d1-d5*cos(q234_1)-d6*sin(theta5_1)*sin(q234_1)-a3*cos(theta2_1));
q23_2 = atan2(-px*cos(theta1_1)-py*sin(theta1_1)-d5*sin(q234_1)+d6*sin(theta5_1)*cos(q234_1)-a3*sin(theta2_2),pz-d1-d5*cos(q234_1)-d6*sin(theta5_1)*sin(q234_1)-a3*cos(theta2_2));
q23_3 = atan2(-px*cos(theta1_1)-py*sin(theta1_1)-d5*sin(q234_2)+d6*sin(theta5_2)*cos(q234_2)-a3*sin(theta2_3),pz-d1-d5*cos(q234_2)-d6*sin(theta5_2)*sin(q234_2)-a3*cos(theta2_3));
q23_4 = atan2(-px*cos(theta1_1)-py*sin(theta1_1)-d5*sin(q234_2)+d6*sin(theta5_2)*cos(q234_2)-a3*sin(theta2_4),pz-d1-d5*cos(q234_2)-d6*sin(theta5_2)*sin(q234_2)-a3*cos(theta2_4));
q23_5 = atan2(-px*cos(theta1_2)-py*sin(theta1_2)-d5*sin(q234_3)+d6*sin(theta5_3)*cos(q234_3)-a3*sin(theta2_5),pz-d1-d5*cos(q234_3)-d6*sin(theta5_3)*sin(q234_3)-a3*cos(theta2_5));
q23_6 = atan2(-px*cos(theta1_2)-py*sin(theta1_2)-d5*sin(q234_3)+d6*sin(theta5_3)*cos(q234_3)-a3*sin(theta2_6),pz-d1-d5*cos(q234_3)-d6*sin(theta5_3)*sin(q234_3)-a3*cos(theta2_6));
q23_7 = atan2(-px*cos(theta1_2)-py*sin(theta1_2)-d5*sin(q234_4)+d6*sin(theta5_4)*cos(q234_4)-a3*sin(theta2_7),pz-d1-d5*cos(q234_4)-d6*sin(theta5_4)*sin(q234_4)-a3*cos(theta2_7));
q23_8 = atan2(-px*cos(theta1_2)-py*sin(theta1_2)-d5*sin(q234_4)+d6*sin(theta5_4)*cos(q234_4)-a3*sin(theta2_8),pz-d1-d5*cos(q234_4)-d6*sin(theta5_4)*sin(q234_4)-a3*cos(theta2_8));
% 关节3
theta3_1 = q23_1 - theta2_1;
theta3_2 = q23_2 - theta2_2;
theta3_3 = q23_3 - theta2_3;
theta3_4 = q23_4 - theta2_4;
theta3_5 = q23_5 - theta2_5;
theta3_6 = q23_6 - theta2_6;
theta3_7 = q23_7 - theta2_7;
theta3_8 = q23_8 - theta2_8;
% 关节4
theta4_1 = q234_1 - q23_1;
theta4_2 = q234_1 - q23_2;
theta4_3 = q234_2 - q23_3;
theta4_4 = q234_2 - q23_4;
theta4_5 = q234_3 - q23_5;
theta4_6 = q234_3 - q23_6;
theta4_7 = q234_4 - q23_7;
theta4_8 = q234_4 - q23_8;
theta_STD = [
theta1_1,theta2_1,theta3_1,theta4_1,theta5_1,theta6_1;
theta1_1,theta2_2,theta3_2,theta4_2,theta5_1,theta6_1;
theta1_1,theta2_3,theta3_3,theta4_3,theta5_2,theta6_2;
theta1_1,theta2_4,theta3_4,theta4_4,theta5_2,theta6_2;
theta1_2,theta2_5,theta3_5,theta4_5,theta5_3,theta6_3;
theta1_2,theta2_6,theta3_6,theta4_6,theta5_3,theta6_3;
theta1_2,theta2_7,theta3_7,theta4_7,theta5_4,theta6_4;
theta1_2,theta2_8,theta3_8,theta4_8,theta5_4,theta6_4;
]*180/pi
由于MATLAB中机器人工具箱对运动学逆解仿真度不够,为此用我自己的模拟机器人测试。没有仿真平台的同学,可以用其他机器人工具箱代替。或其它测试方法。
测试数据1:
图中左边6个参数代表机器人的末端姿态(输入参数),右边6个参数代表6个关节角度(结果)。

MATLAB计算结果1:

测试数据2:

MATLAB计算结果2:

测试数据3:

MATLAB计算结果3:

在工业控制中,由于连杆的DH参数不准确,因此并不能直接将解析解得到的逆解角度直接发送到机器人进行控制,会导致很大的误差, 工业控制中会将机器人进行参数辨识获得准确的DH参数,在进行迭代求解的方式获得关节角度。如果想要学习这方面的知识,请仔细阅读我的第六章博客。
【机器人学】6-5.六自由度机器人运动学参数辨识-逆运动学迭代解【附MATLAB代码】
2024-07-15 更新:将求解q2的过程详细化

























 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








