《Real-Time Rendering 4th Edition》读书笔记--简单粗糙翻译 第七章 阴影 Shadows

写在前面的话：因为英语不好，所以看得慢，所以还不如索性按自己的理解简单粗糙翻译一遍，就当是自己的读书笔记了。不对之处甚多，以后理解深刻了，英语好了再回来修改。相信花在本书上的时间和精力是值得的。

———————————————————————————————

属于生命的一切多样性，一切魅力，一切美好，都是由光和影构成的。 

——Mirumo、托尔斯泰

        阴影对于创建真实的图像很重要， 为用户提供了关于对象位置的视觉提示。 本章主要介绍阴影计算的基本原理，并描述了最重要和最流行的实时算法。 我们还简要讨论了不太流行但体现了重要原则的方法。

        本章中使用的术语如图7.1所示，其中遮光板（occluder）是把阴影投射到接收器（receivers）上的物体。如果使用精准光源（punctual light source），即没有区域，会生成完全阴影区域，有时被称为硬阴影（hard shadows）。 如果使用面积或体积光源，则会产生软阴影（soft shadows）。 每个阴影可以有一个完全阴影的区域，称为本影（umbra）和一个部分阴影的区域，称为半影（penumbra）。软阴影可以通过其模糊的阴影边缘来识别。 然而，需要注意的是，如果只是利用一个低通滤波对硬阴影的边缘进行模糊，通常不能得到正确的渲染结果。如图7.2所示，一个正确的软阴影在接收器上的形状是近似于投射阴影的几何体。 软阴影的本影区域不等于由精准光源产生的硬阴影。 相反，软阴影的本影区域会随着光源变大而减小，如果光源足够大，且接收器距离遮光板足够远，它甚至可能消失。 软阴影效果更好，因为半阴影边缘让观众知道，这里确实是一个阴影。 硬边阴影通常看起来不那么真实，有时会被误解为当前的几何特征，比如表面的折痕。 然而，硬阴影比软阴影渲染速度快。

图 7.1 阴影的术语：光源（light source）、遮光板（ occluder）、接收器（receiver）、阴影（shader）、本影（umbra）、半影（penumbra）

图 7.2 硬阴影和软阴影的混合。 板条箱的阴影很锐利， 因为遮挡者靠近接收器。人的影子在接触点是锐利的， 随着到遮光板的距离增加而软化。 远处的树枝投下柔和的阴影。

         比拥有半影更重要的是要拥有阴影。 没有一些阴影作为视觉提示， 场景往往难以令人信服，也更难理解。 正如Wanger所表明的，有一个不准确的阴影通常比没有更好，因为眼睛对阴影的形状是相当宽容的。 例如，在地板上使用一个模糊的黑色圆圈作为纹理可以将一个角色锚定在地面上。

         在接下来的部分中，我们将超出这些简单的建模阴影，并介绍从场景中的遮挡器实时自动计算阴影的方法。

7.1 平面阴影（Planar Shadows）

        一个阴影发生的最简单例子就是物体在一个平面上投射阴影。 本节介绍了几种用于平面阴影的算法，每种算法在阴影的柔度和真实感方面都有所不同。

7.1.1 投影阴影（Projection Shadows）

        在这个方案中 ，三维物体被渲染了两次来创建一个阴影。通过矩阵计算，把物体的顶点投射到平面上。考虑图7.3所示的情况，光源的位置为l，被投影的顶点是v，投影到平面的顶点是p。先推出投影矩阵的特殊情况下，即阴影平面是y = 0，然后这个结果将推广到任何平面。        

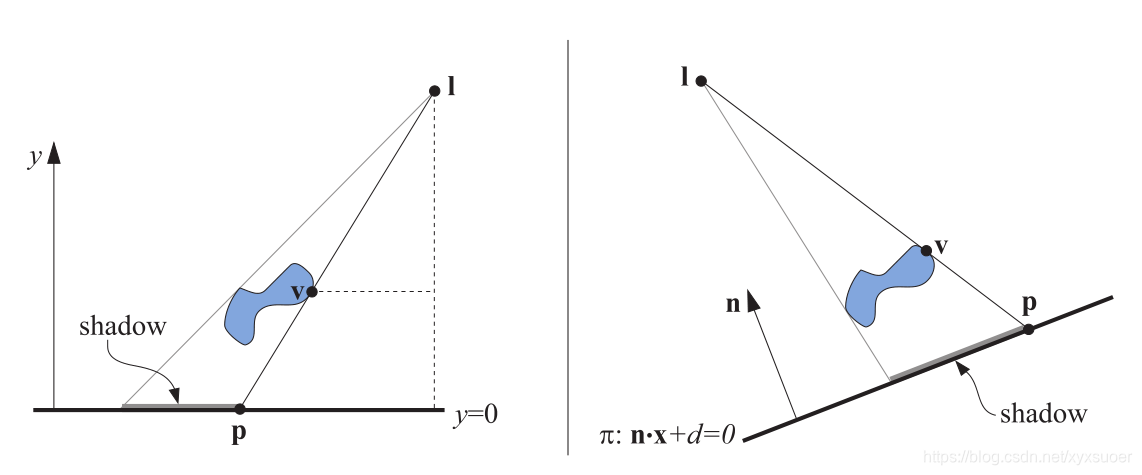
图 7.3 左图：光源在I，投射一个阴影到平面y=0上。顶点v被投影到平面上，对应的投影点是p。两个相似三角形可以用来推导出投影矩阵。右图：在平面π：n·x + d = 0 上的投影。

         我们先求出x坐标的投影，从图7.3左图的相似三角形，我们可以得到：

用同样的方式可以获得z坐标：，同事y坐标为0。然后把这些方程转换成投影矩阵M：

很容易验证Mv = p， 这意味着M确实是投影矩阵。

        在通常情况下，阴影所在平面不是平面y=0，可以用π：n·x+d =0来表示，如图7.3右图所示。 们的目标是找到一个将v投影到p的矩阵。从l发出的射线,经过v,和π平面发生交叉，然后就得到了投影点p：

这个方程也可以转换成一个投影矩阵，如公式7.4所示，满足Mv=p：

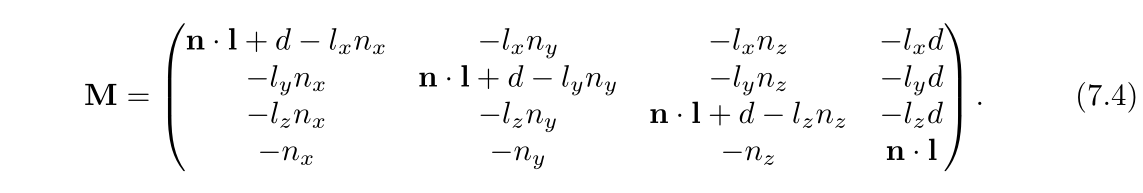
如果平面为y=0，也就是有n=（0,1,0），d=0，公式7.4就变成了公式7.2。

        为了渲染出阴影，简单把这个矩阵应用到物体上，在平面π上投射阴影，然后用黑色并且无光照来渲染这个投影在平面上的阴影。实际操作的时候，需要避免阴影三角形被渲染在接受表面的下方。一种方法是在投影表面上方加一些偏差，这样我们的阴影三角形就永远渲染在表面上方。

         一种更安全的方法是先画出地平面，然后关闭z-buffer，画出阴影三角形，然后像往常一样渲染剩余的几何图形。这些阴影三角形就会永远绘制在地平面上方，因为没有深度比较。

        如果地平面有限制，例如，它是一个矩形，投影阴影可能会落在它之外，打破了视觉错觉。为了解决这个问题，我们可以使用模板缓冲。首先，把接收器绘制到屏幕和模板缓冲中，然后关闭z-buffer，然后绘制只在接收器范围内的阴影三角形，最后正常渲染剩余的场景。

        另外一种阴影算法是把阴影三角形渲染进一张纹理，这个纹理会被应用到地平面上。这个纹理是一种光照贴图（light map）。 正如我们所看到的，这种将阴影投射到纹理上的想法也允许在曲面上产生半阴影和阴影。这种技术的一个缺点是纹理可能被放大，一个纹素可能会覆盖多个像素，打破了视觉错觉。

        如果阴影环境并不是每帧直接发生变化，例如，光源和阴影投射物彼此之间并无移动，这个纹理可以复用。 如果没有发生变化，大多数阴影技术都可以从从一帧到另一帧的中间计算结果的重用中获益。

        所有的阴影发射者必须在光和地平面接收器之间， 如果光源处在物体的最高点下方，会有反阴影（antishadow）发生， 因为每个顶点都是通过光源的点来投影的。 正确的阴影和反阴影如图7.4所示。 如果我们投射一个在接收平面以下的物体，也会发生错误，因为它也不应该投射阴影。

图 7.4 左图展示的是正确的阴影，右图展示的是反阴影， 因为光源在物体的最上面的顶点之下。

         当然可以显式地剔除和修剪阴影三角形，以避免这类瑕疵。 下面介绍一种更简单的方法，即使用现有的GPU管道来执行自带裁剪的投影。

7.1.2 软阴影（soft shadow）

        使用一些技术也可以使投影阴影变成软阴影。在这描述一种Heckbert和Herf提出的算法，这个算法的目的是在地平面生成一张纹理来展示软阴影。

        当光源有一定面积时，就会出现软阴影。 一种近似区域光效果的方法是通过在其表面放置几个精准光源来采样。 对于这些精准光源，都被渲染到一张纹理中并积累到一个缓冲区中。 这些纹理的平均值就是一个软阴影。注意，理论上，任何生成硬阴影的算法都用这类累加技术来生成半影。实际中，以交互的频率来做这类事情是站不住的，因为执行时间也需要考虑到。

        Heckbert和Herf使用了一种基于平截头体的方法来生成阴影。思想就是把光源当作观察者，地平面当作平截头体的远裁剪平面。 截锥体做得足够宽，以包围遮挡板。

        软阴影纹理是通过生成一系列的地平面纹理而形成的，以区域光源上不同的采样点为当前光源，对物体进行投影阴影到渲染到地平面纹理上。然后把这些纹理加起来进行求平均值，这个平均值就是我们要的阴影纹理，图7.5左图就是一个示例。

图 7.5  左图是采用的Heckbert和Herf的算法，使用了256个pass，右图采用的是Haines的算法，使用了一个pass。Haines的算法的本影太大了，尤其是在窗户和门处。

        对区域光源进行采样的算法的一个问题就是它看起来像它本来的样子:几个重叠的影子来自精准光源。同时 ，对n个阴影pass，只生成了n+1个明显的阴影。 大量的传递可以得到准确的结果，但是付出的代价太高。

        一个更高效的方法是使用卷积（convolution），即滤波。 在某些情况下，模糊单一点产生的硬阴影就足够了，并且可以产生半透明的纹理，可以与真实世界的内容混合。如图7.6所示。 然而，在物体与地面接触的地方，一个统一的模糊是无法令人信服的。

图 7.6 下落的阴影（Drop Shadow）。 阴影纹理是通过从上往下渲染出物体的阴影，然后模糊纹理，再渲染到地平面上。

        还有一些其他的方法可以获得更好的近似效果，但是需要额外的成本。例如，Haines算法是先算出一个硬阴影，然后渲染轮廓的梯度边缘，从黑暗的中心到白色的边缘，创造似是而非的半阴影。如图7.5右图所示。然而，这些半阴影不是物理正确的， 因为它们也延伸到了轮廓边缘内的区域。 所有这些方法都有不同的近似值和缺点，但是比平均一组大的阴影纹理要有效得多。

7.2 曲面上的阴影（Shadows on Curved Surfaces）

         将平面阴影扩展到曲面的一个简单方法是使用生成的阴影纹理作为投影纹理。从光源方向考虑阴影。 光能看见的，就能被照亮;它看不见的东西则在阴影里。 假设遮光板从光源方向上被渲染到另外一张白色纹理上。 这个纹理可以投射到接收阴影的表面上。在接收器上的每个顶点有一个(u,v)纹理坐标用于计算它，且纹理应用会用到它。 应用程序可以显式地计算这些纹理坐标。 这与前一节中的地面阴影纹理稍有不同，在前一节中，物体被投射到特定的物理平面上。 在这里，纹理是从光的角度拍摄的，就像投影机里的一帧胶片。

        当渲染时，投影阴影纹理会修改接受器表面， 它也可以与其他阴影方法相结合，有时主要用于帮助感知到物体的位置。 例如，在一个平台跳跃的视频游戏中，主角可能总是被直接赋予一个Drop阴影，即使角色处于完全的阴影中。

        纹理投影方法存在一些严重的缺陷。首先，应用程序必须识别哪些对象是遮光板，哪些对象是它们的接收者。 接收器必须由程序维护，使其比遮光板离光更远，否则阴影就会“向后投射（cast backward）”。另外，遮光板并不能给自己阴影。

         注意，可以通过使用预构建投影纹理来获得各种光照模式。 聚光灯是一个简单的方形投射纹理，它的内部有一个圆圈来定义光线。

7.3     阴影体（Shadow Volumes）

         Heidmann在1991年提出了一种基于Crow 's shadow volume的方法，该方法巧妙地利用模板缓冲区将阴影投射到任意物体上。 它可以用于任何GPU，因为唯一的要求是模板缓存。 它不是基于图像的，从而避免了采样问题，从而可以产生正确的尖锐阴影。 这有时可能是一个不利因素。 例如，一个角色的衣服可能会有褶皱，产生稀薄、坚硬的阴影，会有严重的混叠。 由于其不可预测的成本，体积阴影现在很少被使用。我们在这里对算法进行了简要的描述，因为它说明了一些重要的原则和基于这些原则的研究。

        首先，想象一个点和一个三角形。 把线穿过这个点以及该三角形的顶点，并延伸到无限远处，就得到了一个无限的三面金字塔。 三角形下面的部分，即不包括点的部分，是一个截断的无限金字塔，而上面部分只是一个金字塔，见图7.7。现在假设这个点是光源， 然后，在被截断的金字塔体(三角形下方)内的物体的任何部分都处于阴影中。这个体积被称为阴影体。

图 7.7  左图:点光源的光线通过三角形的顶点延伸，形成一个无限的金字塔。 右图:上半部分为金字塔，下半部分为无限截形金字塔，也称阴影体。所有在阴影体内的几何图形都在阴影中。

         假设我们查看某个场景，并通过一个像素跟踪来自眼睛的光线，直到光线击中要在屏幕上显示的对象。 当光线到达这个物体时，当它穿过正对着的阴影体的一个面时(即，面向观众)，我们给一个计数器加一。因此，每次射线进入阴影计数器是递增的。 以同样的方式，每次射线穿过截形金字塔的背面时，我们给计数器减一，光线会从阴影中消失。 我们持续对计数器进行递增和递减，直到射线击中的物体需要显示的那个像素。 如果计数器大于0，则该像素处于阴影中;否则就不是。 这个原则也适用于有多个三角形投射阴影的情况。参见图7.8。

图 7.8   使用两种不同的计数方法计算阴影-体积交叉点的二维侧视图。在z-pass体积计数中， 当光线通过阴影体的前面（frontfacing）三角时，计数递增;当光线通过后面（backfacing）三角时，计数递减。因此，在点A，射线进入了两个阴影体，计数为+2，然后离开了两个阴影体，计数清零，所以这个点在光中。在z-fail体计数中， 计数从表面开始(这些计数以斜体显示)。在B点处的射线，z-pass方法给出的计数为+2（穿过了两个前面三角形），z-fail给出了相同的计数（穿过了两个后面三角形）。点C展示了z-fail阴影体积必须要有上限。 射线从点C出发，首先击中前面三角形，给出了- 1。 然后，它退出两个阴影体积（通过它们的结束端，这是此方法正常工作所必需的)，净计数为+1。计数不为0，所以这个点在阴影中。 这两种方法对所观察的表面上的所有点都给出相同的计数结果。

         用射线做这件事很费时间。 但还有一个更聪明的解决方案： 模板缓冲可以帮我们计数。 首先，清除模板缓冲区， 其次，整个场景被绘制到帧缓冲中，只使用无光照材质的颜色，以获得颜色缓冲区中的这些着色组件和z-buffer中的深度信息。 第三，关闭z-buffer的更新和写入颜色缓冲区(尽管z缓冲测试仍在进行)，然后绘制阴影体积的前面三角形。 在此过程中，增加在模板缓冲中需要绘制三角形的位置的值。 第四步，在另外一次Pass渲染过程中使用模板缓冲区再完成一次，这一次只绘制阴影体积的背面三角形。 在这次Pass中，模板缓冲区中绘制三角形的位置的值将递减。 当计数的加减都完成后，只有阴影体需要渲染的表面的像素是可见的(即不是被任何真实的几何图形所隐藏)。 在这一点上，模板缓冲区保持每个像素的阴影状态。 最后，再次渲染整个场景，这次只使用受光线影响的材质组件，并且只显示模板缓冲区中值为0的地方。 值为0表示射线从阴影中消失的次数与进入阴影体积的次数相同，这个位置被光照亮。

         这种计数方法是阴影体背后的基本思想。 阴影体算法生成的阴影示例如图7.9所示。 有一些有效的方法可以只使用一次Pass就可以实现算法， 然而，当一个物体穿透相机的近平面时，计数问题就会出现。 一种解决方案称为z-fail，计算的是隐藏在可见表面的背面而不是前面。此方案的简要摘要如图7.8所示。