写在前面的话:因为英语不好,所以看得慢,所以还不如索性按自己的理解简单粗糙翻译一遍,就当是自己的读书笔记了。不对之处甚多,以后理解深刻了,英语好了再回来修改。相信花在本书上的时间和精力是值得的。
———————————————————————————————
“What if angry vectors veer Round your sleeping head, and form. There’s never need to fear ,Violence of the poor world’s abstract storm.”—Robert Penn Warren
“若疯狂的矢量的运算,纠缠着你昏昏欲睡的大脑,掀起抽象世界的风暴,不要畏惧!干就完了!" —王大伟
变换(Transform)是一种操作,针对的是点,向量或颜色值,以某种方式进行转换。对于计算机图形操作者而言,掌握变换极其重要。利用好这种操作,你可以对物体进行光照,对摄像机进行定位,重塑或者触发动画。你还可以把所有计算转换到同一坐标系下,可以用不同的方式把物体投影到一个平面上。
线性变换满足向量加法和标量乘法:

举个例子,f(x)= 5x,是将一个向量的每个元素都乘以5。为了证明这个是线性操作,4.1和4.2的两个条件都需要满足。4.2被称为是缩放变换(Scaling transform),因为它可以改变一个物体的大小(尺寸)。旋转变换(Rotation transform)也是一个线性变换,旋转变换会将一个向量绕着原点进行旋转。缩放变换和旋转变换,以及所有针对三元素向量的线性变换,都可以用一个3x3的矩阵表示。
然而,3x3通常不够大。例如,f(x) = x + (7,3,2)不是一个线性变换,其中x是一个三元素向量,因为按照公式4.1来算,等号左边比等号右边多加了一个(7,3,2)。将一个固定的向量和另外一个向量相加的操作,称为平移。这是一个很重要的操作。通常我们会组合各种变换,例如,先缩小一个物体的一半,然后移动它到另外一个位置。如果使用3x3的矩阵形式来表达的话,不利于我们组合各种变换。
利于一种仿射变换(Affine transform),通常用4x4的矩阵来存储,可以将线性变换和平移组装到一块。仿射变换通常是先进行线性变换,然后再进行平移变换。用齐次坐标来表示四元素向量,点和方向向量可以用同一种表达式。方向向量可以用![]() 表示,点可以用
表示,点可以用![]() 表示。所有的平移矩阵,旋转矩阵,缩放矩阵,反射矩阵和剪切矩阵都是仿射矩阵。
表示。所有的平移矩阵,旋转矩阵,缩放矩阵,反射矩阵和剪切矩阵都是仿射矩阵。
本章从最基础的基本仿射变换开始。表4.1总结了大部分这些变换、符号、函数和属性。其中,正交矩阵的转置矩阵就是其逆矩阵。

表4.1 本章中讨论的大部分变换的总结
变换可以说是操作几何图形的基本工具。大多数图形API是允许用户设置任意矩阵的,以及一些含有很多矩阵操作的库。然而,还是很值得去理解这些库和API后面的矩阵操作。知道一个API功能的使用只是个开始,了解后面矩阵操作才会使得你走的更远。例如,知道正交矩阵的逆矩阵就是它的转置矩阵,会让你的代码更简单更快速。
4.1 基本变换
4.1.1 平移


4.1.2 旋转

在3D领域中,通常用Rx(φ), Ry(φ), and Rz(φ)来表示旋转矩阵,分别表示沿着x,y,z轴进行旋转。如下公式4.5-4.7:

旋转矩阵的效果见于图4.4。旋转矩阵有两个特征,一是它绕着i轴(x,y,z)旋转,二是i轴上所有点保持不变。注意,旋转矩阵也可以用来表示绕任意轴的旋转矩阵,可以利用上面三个旋转矩阵组合得到绕任意轴的旋转矩阵,这些将在4.2.1和4.2.4中进一步讲到。
所有的旋转矩阵的行列式都为1,并且是正交矩阵。这就使得任意数量的旋转变换都可以级联在一起。可以通过![]() 来表示旋转矩阵的逆矩阵,绕着同一个轴进行反方向旋转。
来表示旋转矩阵的逆矩阵,绕着同一个轴进行反方向旋转。
例子:绕点旋转。假设围绕z轴旋转![]() ,旋转的中心点为P,如图4.2所示。因为围绕P旋转,所以P不动。变换第一步是平移物体,利用平移矩阵T(-p)将p平移到原点处,然后旋转物体,利用旋转矩阵
,旋转的中心点为P,如图4.2所示。因为围绕P旋转,所以P不动。变换第一步是平移物体,利用平移矩阵T(-p)将p平移到原点处,然后旋转物体,利用旋转矩阵![]() 进行旋转操作,最后利用平移矩阵T(P)将物体移回到原始位置。最终结果为
进行旋转操作,最后利用平移矩阵T(P)将物体移回到原始位置。最终结果为

4.1.3 缩放
缩放矩阵![]() ,将一个物体以Sx,Sy,Sz的比例分别对x轴,y轴,z轴进行缩放。这意味着缩放矩阵可以放大或缩小物体。缩放因为Si,
,将一个物体以Sx,Sy,Sz的比例分别对x轴,y轴,z轴进行缩放。这意味着缩放矩阵可以放大或缩小物体。缩放因为Si,![]() ,越大,对应轴向的缩放比例越大。如果缩放因子为1,那么该方向不会进行缩放。4.10为缩放矩阵:
,越大,对应轴向的缩放比例越大。如果缩放因子为1,那么该方向不会进行缩放。4.10为缩放矩阵:
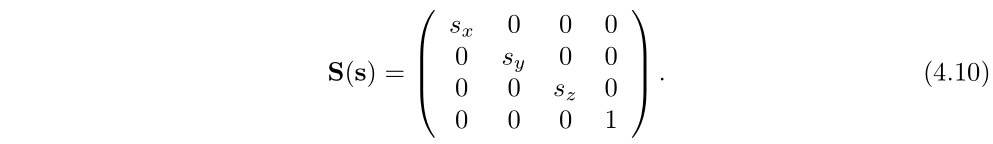
图4.4 展示了缩放矩阵的作用。如果Sx=Sy=Sz,称为统一变换(uniform),否则称为非统一变换(nonuniform)。有时候也称为各向同性(isotropic)和各向异性(anisotropic)。逆矩阵![]() 。
。
当使用齐次坐标系时,还有一种方式表示统一缩放矩阵,就是利用矩阵位于(3,3)(右下角)的值。这个值会影响齐次坐标系中W值,进而通过W值影响到点的每个轴向的变换,对统一缩放矩阵的方向无效。如下两种方式表示:

和S矩阵相比,S'必须是齐次操作。这可能会比较低效,因为齐次操作中引入了除法,如果右下角的值为1,则不需要进行除法。当然,有些系统是不会去判断是否值为1,因为这样可减少额外的消耗。
如果S中一个元素或者三个元素为负数时,则称为反射矩阵(reflection),或者称为镜像矩阵(mirror)。如果只有两个元素值为-1,则会物体被旋转π。注意,一个旋转矩阵乘以一个反射矩阵,结果仍然是一个反射矩阵。例如:

反射矩阵通常需要进行特殊处理。例如,反射矩阵处理一个逆时针三角形后,会变成一个顺时针三角形。这个顺序的变化可能会导致错误的光照和隐面消除。为了检测出是否为一个反射矩阵,可以先算出左上3x3的行列式。如果行列式为负,则该矩阵是反射矩阵。如4.12所示,0·0 -(-1)·(-1) = -1。
例子:沿着一个特定方向进行缩放。标准缩放矩阵只针对x,y,z轴进行了缩放,如果需要做一个 特定方向上的缩放,需要进行复合变换。假设需要沿着正交坐标系![]() ,
,![]() 和
和![]() 进行缩放,则第一步是先构建出F矩阵,如下
进行缩放,则第一步是先构建出F矩阵,如下
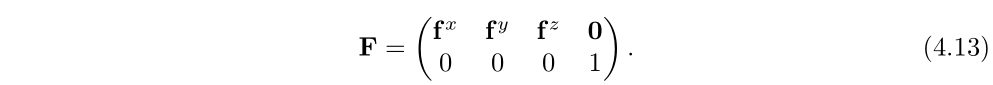
有了F矩阵,则变换就是先把标准坐标系下的坐标转换到新坐标系下,然后进行缩放变换,最后把坐标转移回来。公式如下
![]()
4.1.4 切变
有一种变换叫切变变换,例如,在游戏中利用切变变换可以扭曲整个游戏场景以制造一种迷幻效果,或者扭曲物体的外观。有6个基本切变矩阵,分别为
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 。第一个下标表示的是切变矩阵改变的坐标,第二个下标表示的是切变变换使用的坐标。如公式4.15所示,
。第一个下标表示的是切变矩阵改变的坐标,第二个下标表示的是切变变换使用的坐标。如公式4.15所示,![]() 表示的是切变矩阵,很明显可以从下标中找到参数s,x表示的是第0行,z表示的是第2列,则S位于第0行和第二列的交叉处。
表示的是切变矩阵,很明显可以从下标中找到参数s,x表示的是第0行,z表示的是第2列,则S位于第0行和第二列的交叉处。

将![]() 和点P相乘得到新点P'
和点P相乘得到新点P'![]() 。图4.3展示了一个方块切变变换后的效果。
。图4.3展示了一个方块切变变换后的效果。![]() (i 不等于j)的逆矩阵为其反方向的切变矩阵,
(i 不等于j)的逆矩阵为其反方向的切变矩阵,![]() 。
。

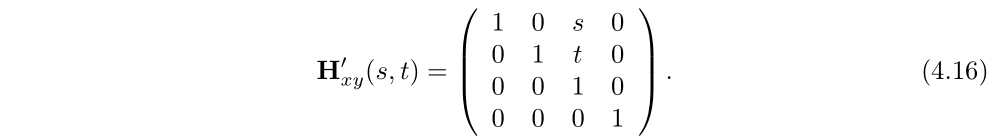
4.1.5 变换结合
由于矩阵乘法中的不可交换性,矩阵的顺序很重要,在变换串联的时候也是基于顺序的。
假设有两个矩阵,S(2,0.5,1)和Rz(π/6)。S表示将x坐标乘以2,y坐标乘以0.5,z坐标不变,R表示沿着z轴(右手坐标系中,垂直平面指向外面的轴)逆时针旋转 π/6。如图4.4所示,两种顺序进行串联得到的结果不同。

图4.4 矩阵相乘顺序不同的例子。上面表示的是![]() ,先进行旋转然后再缩放。下面表示的是
,先进行旋转然后再缩放。下面表示的是![]() ,先进行缩放,然后再进行旋转。可见结果不同,有矩阵的不可交换性
,先进行缩放,然后再进行旋转。可见结果不同,有矩阵的不可交换性![]() 。
。
串联矩阵的作用在于提高效率,举个例子,一个游戏场景中有几百万个顶点,在场景中的全部物体都需要进行缩放,旋转,然后平移。如果将每个顶点分别和这三个变换矩阵进行变换,不如将三个变换矩阵串联成一个矩阵,然后用来和顶点做变换处理。则串联后的矩阵为![]() 。注意,这里的顺序。首先进行的是缩放变换,所以S出现在最右侧。所以有
。注意,这里的顺序。首先进行的是缩放变换,所以S出现在最右侧。所以有![]() ,其中P表示的是需要变换的顶点。基本上TRS是图形系统中最为常见的顺序。
,其中P表示的是需要变换的顶点。基本上TRS是图形系统中最为常见的顺序。
值得注意的是,因为矩阵是顺序串联在一起的,所以可以对其进行分组计算。例如在进行刚体运算的时候,可以将TR进行结合,所以有TRSp=(TR)(Sp)。可见矩阵串联满足结合定律。
4.1.6 刚体变换
当一个人抓住一个实物,例如桌子上的一支笔,从一个地方移动到另外一个地方,例如衬衫的口袋里,只有实物的方向和位置发生了变化,实物的形状没有任何变化。这样的变换,只是结合了旋转和平移,被称为刚体变换。它的特性是保持了物体本身的长度、角度和对称性。
用T(t)表示平移矩阵,R表示旋转矩阵,X表示刚体矩阵,那么有

X的逆矩阵有![]() 。也就是说计算X的逆矩阵,只需要转置R左上的3x3矩阵,平移矩阵T改变符号,然后将两个新矩阵按与原相乘的相反顺序相乘。还有一种计算X的逆矩阵,首先用下面的公式4.18表达X。
。也就是说计算X的逆矩阵,只需要转置R左上的3x3矩阵,平移矩阵T改变符号,然后将两个新矩阵按与原相乘的相反顺序相乘。还有一种计算X的逆矩阵,首先用下面的公式4.18表达X。

其中![]() 表示旋转矩阵的第一列,
表示旋转矩阵的第一列,![]() 表示旋转矩阵的第一行。注意
表示旋转矩阵的第一行。注意![]() 表示的是一个3x1的列向量,每个元素值都为0。所以X的逆可以表达为
表示的是一个3x1的列向量,每个元素值都为0。所以X的逆可以表达为

例子:摄像机的方向。图形学中一个常见的操作是旋转摄像机的朝向,使之对准一个方向。这里使用函数gluLookupAt()(来自OpenGL Utility库,简称 GLU)。尽管这个函数如今不怎么使用了,但是这个需求还是很常见。假设摄像机位于c,需要摄像机对准I,并给定了世界空间向上的向量u',如图4.5所示。需要计算一个基坐标系{r,u,v}。首先计算出视觉方向![]() ,从摄像机指向目标对象的归一化向量。摄像机朝向所对应的朝右方向有
,从摄像机指向目标对象的归一化向量。摄像机朝向所对应的朝右方向有![]() 。u'通常不能表示摄像机朝上向量,最终的向上向量还是通过计算
。u'通常不能表示摄像机朝上向量,最终的向上向量还是通过计算![]() ,v和r叉积得到,由于v和r都已归一化,则u也是归一化的,并相互垂直。接下来构造摄像机的变换矩阵M,首先将摄像机的位置归零,然后改变基坐标系,将r对应为(1,0,0),u对应为(0,1,0),v对应为(0,0,1)。
,v和r叉积得到,由于v和r都已归一化,则u也是归一化的,并相互垂直。接下来构造摄像机的变换矩阵M,首先将摄像机的位置归零,然后改变基坐标系,将r对应为(1,0,0),u对应为(0,1,0),v对应为(0,0,1)。
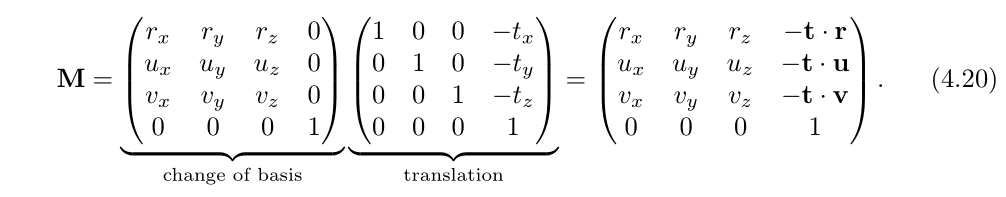

4.1.7 法线变换









 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








