《Real-Time Rendering 4th Edition》读书笔记--简单粗糙翻译第五章着色基础 Shading Basics

本文链接：https://blog.youkuaiyun.com/xyxsuoer/article/details/104481161

写在前面的话：因为英语不好，所以看得慢，所以还不如索性按自己的理解简单粗糙翻译一遍，就当是自己的读书笔记了。不对之处甚多，以后理解深刻了，英语好了再回来修改。相信花在本书上的时间和精力是值得的。

———————————————————————————————

”你需要做的是渲染出一张好图片“

当你需要渲染一个三维对象时，模型不仅需要合适的几何形状，还需要有合适的视觉外观。根据应用程序的不同，其范围可以从照片写实（外观几乎和真实物体的照片一样）到出于创造而选择的各种风格化外观。如图5.1所示两种例子。

图 5.1 上图是用虚幻引擎渲染的写实山水场景。而下图的渲染用的是Campo Santo，这是专门用来渲染插图风格类型的。

5.1 着色模型（Shading Models）

渲染一个物体外观的第一步是选择一个着色模型，用表面朝向，观察方向，光照等因素来决定物体的颜色。

我们以Gooch着色模型（Gooch Shading model）的一个变种为例。这是第15章讨论的非真实感渲染的一种形式，Gooch着色模型旨在提高技术插图细节的清晰度。

Gooch着色模型背后的基本思想是将表面的法线和光源的位置进行比较，如果法线指向光源，则使用暖色调为表面着色，相反则使用冷色调。介于两者之间角度则用插值。在这个例子中，我们添加了一种“高光（highlight）”效果来使物体外形具有光泽度。图5.2展示了Gooch着色模型的实际效果。

图 5.2 结合了Gooch着色模型和高光效果的风格化着色模型。上图展示了具有中性表面颜色的复杂模型，下图展示的是使用各种不同表面颜色的材质球。

着色模型通常有可以控制外观变化的属性。渲染一个物体外观的第二步就是设置这些属性值。本例中，渲染模型只有一个属性，即表面颜色，如图5.2下图所示。

和大部分着色模型一样，本例也受到相对于观察方向和光照方向的表面朝向的影响，出于着色目的，这些方向通常用归一化（单位长度）向量表示，如图5.3所示。

图 5.3 本例着色模型（其实大部分着色模型）的输入用单位向量表示，表面法线 n，观察向量 v，光照方向 l。

现在我们已经定义好了着色模型的全部输入，接下来可以看下着色模型的数学定义：

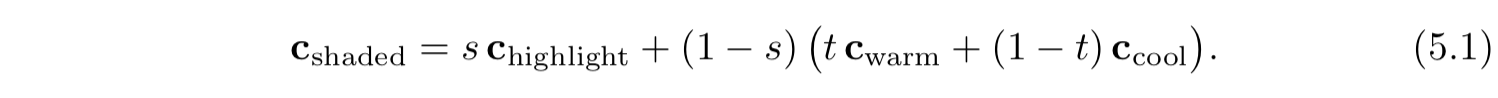
在等式中，采用了以下一些中间计算：

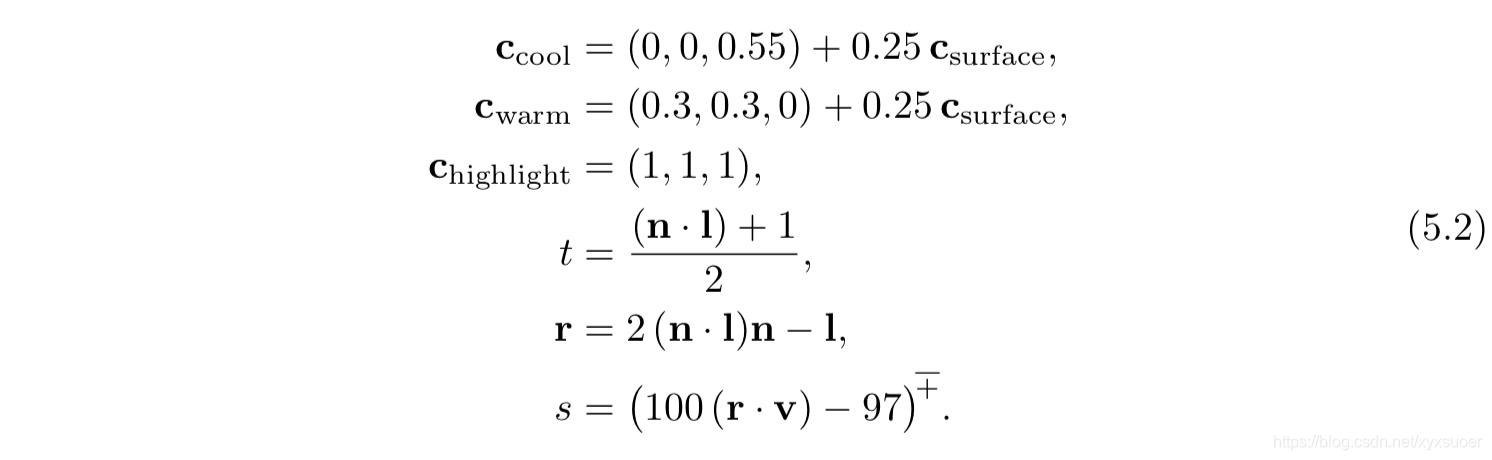
该定义中的一些数学表达式也经常在其他的着色模型中见到， Clamping操作在着色中经常用到，常见的是clamp到0或者clamp到0和1之间。在这里我们用1.2节所介绍的

符号来表示计算高光混合因子s需要clamp在0和1之间。点积运算符出现了三次，每次出现在两个单位向量之间，这是一种很常见的模式。两个向量的点积是它们的长度和它们之间夹角的余弦的乘积。所以，单位向量的点积就是它们之间夹角的余弦。由余弦组成的简单函数通常是用来表达两个方向之间关系的最准确也最好的数学表达式，例如本例中的光方向和表面法线之间的关系。

着色中另外一个常见操作是对颜色（在0和1之间）进行线性插值。这个操作采用

这种方式，在Ca和Cb之间进行插值，随着t从1到0变化，插值结果从Ca到Cb。这个模式在Gooch着色模型中出现了两次，第一次是在Cwarm和Ccool之间进行插值，第二次是将先前插值结果和Chighlight进行插值。线性插值在着色中出现频率很高，在着色语言中有内置函数，称为lerp或者mix。

“ r = 2 ( n · l ) n − l ”是计算反射光向量，计算l关于n的反射。尽管不像上两个操作（clamp和lerp或mix）出现的那么频繁，但是一般着色语言中也有内置反射功能。

通过将这些操作以不同的方式同各种数学表达式和着色参数值组合在一起，可以为多种风格化外观和写实外观定义着色模型。

5.2 光源（Light Sources）

本例着色模型中光照的影响很简单，仅提供了一个主要方向。当然，在现实世界中光照很复杂，可以有多个光源，每个光源都有自己的尺寸，形状，颜色和强度，如果加入间接光照则会有更多变化。在第九章，基于物理的真实感着色模型需要考虑到所有这些参数。

根据应用程序和视觉风格的需要，各种风格化的着色模型可以以多种不同方式使用光照。一些高度风格化的着色模型可能根本就没有光照概念，或仅仅用来提供一个简单的方向性（例如Gooch着色模型）。

着色模型中光照的复杂性也反映在，以二进制形式对光的存在或不存在作出反应。着色模型在有光照的情况下会展示一种外观，在没有光照的情况下将具有不同的外观。这暗示了区分两种情况的一些标准：距光源的距离、阴影（第七章讲到）、表面是否背对光源（表面法线n和光线向量l之间的夹角大于90度）或这些因素的组合。

从以二进制形式表示光的存在或不存在到光强度的连续范围都是一小步，可以用不存在和完全存在之间的简单插值表示，这表示对强度是一个有界范围，可以从0到1，或者表示为以某种方式影响着着色的无边界量。后者的常见操作是将着色模型分成有光照和无光照两部分，光强度Klight线性缩放有光照部分：

这可以容易拓展到一个RGB光颜色Clight，

和多光源，

无光照部分funlit(n,v) 对应于将光视为二进制的着色模型的“不受光影响时的外观”。它可以有各种各样的形式，取决于所需要的视觉风格和应用程序所需。例如 funlit() =(0，0，0)将使不受光源影响的任意表面以纯黑色表示。当然，无照明部分也可以为无照明物体表达某种形式的外观，类似于Gooch着色模型的背向光源的冷色。通常着色模型表示有光照部分的光源并非直接来自某个明确放置的光源，例如来自天空的光或来自周围物体的反射光。这些光的形式将在第十章和第十一章讨论。

前面提到的，如果光的方向和表面法线的夹角大于90度，则光源不会影响表面上的点，实际上是影响表面的背面。这可以看作是相对于表面的光方向和光对着色的影响之间关系的一个特例。尽管是基于物理的，这个关系可以从简单的几何原理派生而来，对许多非基于物理的着色模型和风格化着色模型很有用。

可以将光作用于表面的效果可视化为一组射线，其中射线击中表面的密度对应于表面着色中的光强度。如图5.4所示，该图显示了一个光照表面的横截面。沿该横截面入射到表面的光线与表面的交点之间的距离与l和n之间的角度的余弦成反比。因此，入射到表面的光线的总密度与l和n之间角度的余弦成比例，正如前面说到的，等于两个单位向量的点积。在这里，可以看到为什么定义光向量的方向和光的传播方向相反了，否则我们不得不在点积运算之前对其进行取反。

图 5.4 上面一排展示的是光击中表面的横截面的示意图，左图的光线是垂直击中表面，中间图光线以一个倾角击中表面，右图展示的是用向量的点积来计算向量夹角的余弦。下图展示的是在表面上的某一个横截面。

更准去的说，当点积为正时，光线密度和点积结果成正比，负值对应于从表面背面发出的光线，是无效的。因此在着色公式中，需要将点积保证大于0，用

来表示（1.2节中介绍），这意味着点积为负值则取零。则有：

支持多光源的着色模型通常使用的是公式5.5（更通用）或公式5.6（需要基于物理的模型）。公式5.6对于一些风格化着色模型也有用，因为它可以帮助确保光照的整体一致性，特别是对于背离光源或处于阴影中的表面。当然也有一些并不是适用，而这些模型则可以使用公式5.5。

函数flit()最简单的选择是使用一个常量颜色，

这样着色模型公式为：

这个光照部分对应于 Lambertian着色模型，该模型工作在理想漫反射表面（即完全无光泽的表面）。Lambertain着色模型可以单独用于简单着色，它是许多着色模型的关键组成部分。

从公式5.3到5.6可以看出，一个光源影响着色模型靠两个参数：指向光源的向量l和光颜色Clight。有多种不同类型的光源，它们的主要区别在于这两个参数在场景中的变化方式。

接下来将讨论几种常见的光源，它们有一个共同点：给定了一个表面位置后，每个光源仅从一个方向I照向表面。换句话说，从着色表面位置来看，每个光源都是一个无限小的点。对于现实世界中的光源，这并不严格对，但是大多数光源相对于它们到表面的距离都很小，因此这是一个合理的近似值。

5.2.1 平行光（Directional Lights）

平行光是光源中最简单的模型，在整个场景中I和Clight都是恒定的，除了Clight可能会被阴影影响而衰减。平行光没有位置，当然，实际光源在空间中有一个特定的位置，平行光是抽象的，当光源到场景的距离相对于场景的大小非常大的时候，平行光会表现很好。例如，一个20英尺远的泛光灯可以照亮一个小的桌面西洋镜，则灯可以看作是一个平行光。另外一个例子是凡是被太阳照到的场景，除非所涉及的场景是诸如太阳系内行星之类的东西。

平行光的概念可以稍微扩展下，在允许光方向I不变的情况下，可以改变Clight的值。这通常发生在把光照效果和场景的特定部分绑定的时候，一般是为了表现一些特别效果。例如，有两个嵌套（一个在另外一个内）的立方体盒子，在外部盒子的外部的Clight是（0，0，0），纯黑色，而在内部盒子的内部Clight是某个常量。而在两个盒子之间的采用的是平滑插值得到的结果。

5.2.2 精准光源（Punctual Lights ）

精准光源（Punctual Light）并没有准时的意思（punctual是准时的意思），而是一个具有位置的光照，和平行光不同。和现实中的光不同，这类光没有尺寸，没有形状没有大小。使用术语“Punctual”，是因为在拉丁语中punctus 表示“点，point”。用术语“point light”（点光源）来表示一种特定的发射器， 它可在所有方向上均等的发射光线。 因此点光源和聚光灯（spotlight）是精准光源的两种不同表现形式。光线向量I取决于当前着色表面上的点P0和精准光源Plight：

这个方程是一个向量归一化示例：将向量除以其长度即可产生指向相同方向的单位长度的向量。这也是一个常见的着色操作，在大部分着色语言中都有内置函数。但是，有时候需要这个操作的中间结果，这需要多个步骤，并且要显示执行归一化。

所以有：

我们需要的中间值是r，即精准光源和当前着色表面上的点之间的距离。除了将其用于归一化光向量外，还需要r的值来计算光颜色Clight随着距离的衰减变化（变暗）。这将在下一节讨论到。

点光源/泛光源（Point/Omni Lights）

在所有方向上均匀发射光线的精准光源，称为点光源（Point Lights）或泛光源（Omni Lights）。对点光源，Clight值随着r的增大而衰减。图5.5展示了为什么会衰减，利用了类似于图5.4中的余弦因子进行几何推理。在给定的表面上，来自点光源的光线间的距离和从表面到光源的距离成正比。与图5.4中的余弦因子不同，此间距的增加沿着表面两个维度发生，因此射线密度（及因此引起的光颜色Clight值）与

成正比。这样一来，r就是计算Clight的唯一因素，其中

定义为Clight在固定距离r0处的值：

公式5.11通常被称为 平方反比光衰减（inverse-square light attenuation）。尽管从技术上讲，对点光源是有着正确的距离衰减。但是还有一些问题让这个方程并不适合于实际的着色使用。

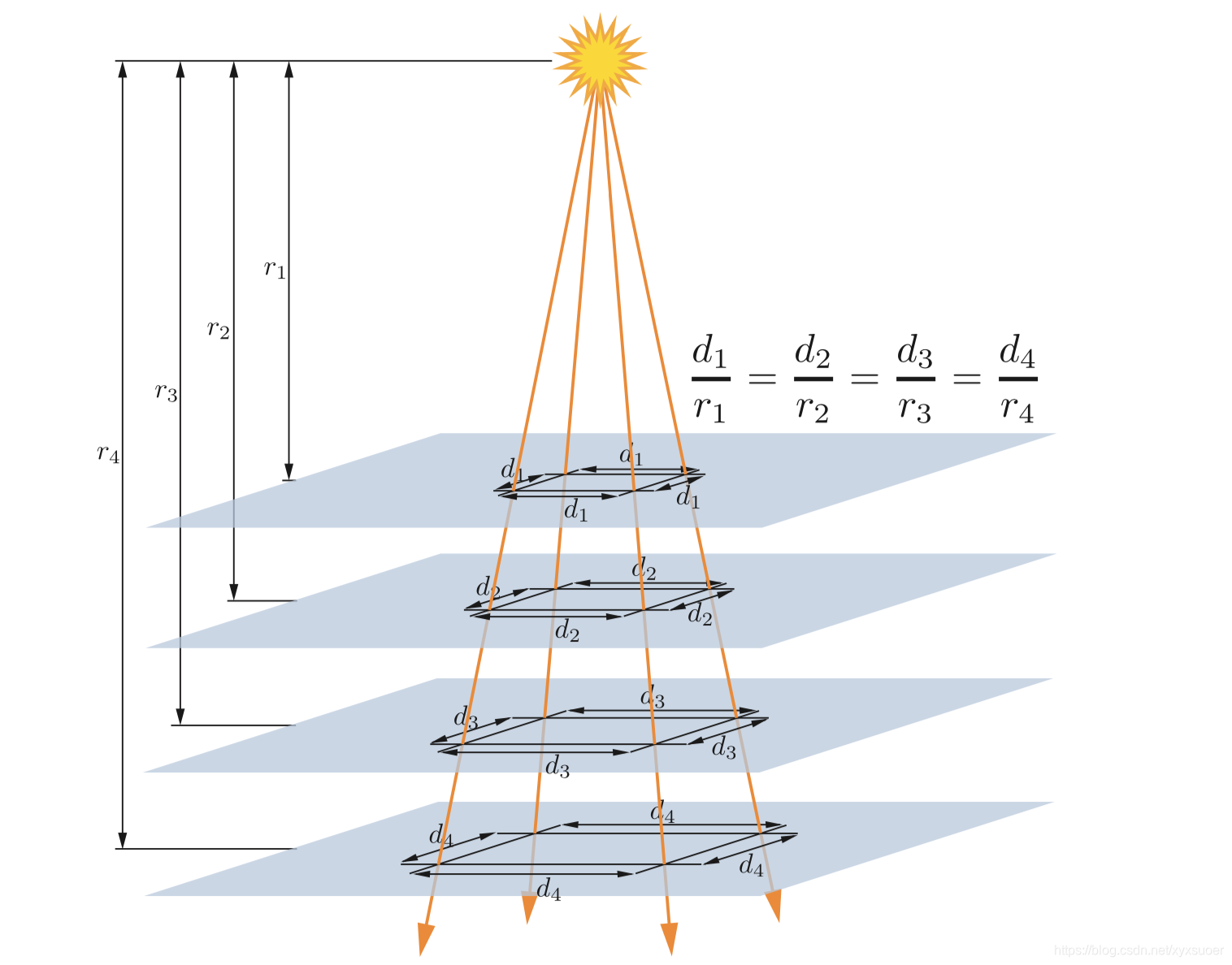
图5.5 点光源发出的光线间的间距与距离r成比例增加，因为光线间的间距同时在二维上增加，因此光线的密度（及光强）和r的平方的反比成正比。

第一个问题发生在相对较小的距离处，随着r趋向于0，Clight的值会增加到无限大，随着r为0时，将得到一个除以0的奇点，为了解决这个问题，一种常见的做法是在分母增加一个小值ε：

ε的确切值取决应用程序， 例如，在虚幻引擎中使用的 ε=1cm。

另外一种方案是（CryEngine和Frostbite 游戏引擎采用的）是把r钳位到一个最小值 rmin ：

和前面采用ε的方法不同， r min 有物理解释：发光物体的半径。对于小于rmin 的r值所对应的是穿透物理光源内部的着色表面，这是不可能的。

相反的，平方反比衰减的第二个问题发生在相对较大的距离处。这个问题不在于视觉效果而在于性能。尽管光强随着距离增加而不断减小，但是永远都到达不了0。为了高效渲染，希望光在某个有限距离处光强为0。这里有许多不同的方法来修改平方反比方程来实现这一目的。理想情况下，修改应该尽可能少的更改。 为了避免在光线影响范围边缘出现明显的截止，建议修改后的函数和该函数的导数在同一距离处值为0。一种解决方案是对平方反比方程乘以 窗口函数（ windowing function ）。虚幻引擎和Frostbite游戏引擎采用的是：