题目描述
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
提示:
- 1 < = n u m s . l e n g t h < = 2500 1 <= nums.length <= 2500 1<=nums.length<=2500
- - 10 4 < = n u m s [ i ] < = 10 4 10^4 <= nums[i] <= 10^4 104<=nums[i]<=104
进阶:
- 你能将算法的时间复杂度降低到 O ( n l o g ( n ) ) O(n log(n)) O(nlog(n)) 吗?
思考一:动态规划
动态规划解法通过定义状态追踪以每个元素结尾的最长递增子序列长度:
dp[i]表示以第i个元素结尾的最长递增子序列长度- 核心逻辑:对于每个元素,比较其与之前所有元素,若当前元素更大,则可基于之前的子序列延长
算法过程
-
初始化:
dp数组全部设为 1(每个元素自身构成长度为 1 的子序列)maxLen初始化为 1(最小可能的最长子序列长度)
-
状态更新:
- 遍历每个元素
i(从 1 到n-1):- 遍历其之前的所有元素
j(从 0 到i-1):- 若
nums[i] > nums[j],则dp[i] = max(dp[i], dp[j] + 1)(基于j结尾的子序列延长)
- 若
- 更新
maxLen为max(maxLen, dp[i])(记录全局最长长度)
- 遍历其之前的所有元素
- 遍历每个元素
-
返回结果:
maxLen即为最长递增子序列的长度
时间复杂度
- 时间复杂度:O(n²),外层循环遍历
n个元素,内层循环对每个元素最多比较n次 - 空间复杂度:O(n),需存储长度为
n的dp数组
该方法通过动态规划暴力枚举所有可能的前序元素,完整覆盖了以每个元素结尾的最长递增子序列情况。
代码
/**
* @param {number[]} nums
* @return {number}
*/
var lengthOfLIS = function(nums) {
const n = nums.length;
const dp = Array(n).fill(1);
let maxLen = 1;
for (let i = 1; i < n; i++) {
for (let j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
maxLen = Math.max(maxLen, dp[i]);
}
return maxLen;
};
思考二:二分查找
传统动态规划(O(n²))会重复比较所有历史元素,而实际上我们只需要关注"对未来扩展最有利"的子序列信息。
"最有利"的定义是:对于长度为k的子序列,其末尾元素越小,未来能拼接的元素就越多。
-
维护一个辅助数组
tailstails[i]表示:所有长度为i+1的递增子序列中,末尾元素的最小值- 这个数组天然具有单调性(严格递增)
-
对每个新元素执行二分查找
- 在
tails中找到第一个大于等于当前元素的位置pos - 若
pos等于tails长度,说明当前元素可组成更长的子序列,直接追加 - 否则,用当前元素替换
tails[pos],确保同长度子序列的末尾元素最小
- 在
-
最终结果
tails数组的长度就是LIS的长度(不必关心具体子序列内容)
算法过程
-
初始化辅助数组:创建空数组
tails,用于记录“长度为i+1的递增子序列的最小末尾元素”(tails[i]对应长度i+1)。 -
遍历原数组元素:对每个元素
nums[i]执行以下操作:- 二分查找位置:在
tails中查找第一个大于等于nums[i]的位置pos(左右指针l=0,r=tails.length-1,通过中间值m调整范围,直至l > r,此时l即为目标pos)。 - 更新辅助数组:
- 若
pos等于tails长度(当前元素大于tails中所有元素),则将其追加到tails(形成更长的子序列)。 - 否则,用
nums[i]替换tails[pos](确保长度为pos+1的子序列末尾元素最小,为后续扩展留更多可能)。
- 若
- 二分查找位置:在
-
返回结果:遍历结束后,
tails数组的长度即为最长递增子序列的长度。
时间复杂度
- 时间复杂度:O(n log n),遍历
n个元素,每个元素的二分查找耗时O(log k)(k为当前tails长度,最大为n)。 - 空间复杂度:O(n),
tails数组最长为n(当原数组完全递增时)。
该方法通过维护“最小末尾元素”数组和二分查找,大幅优化了时间效率,是LIS问题的最优解法之一。
代码
/**
* @param {number[]} nums
* @return {number}
*/
var lengthOfLIS = function(nums) {
const n = nums.length;
const tail = [];
for (let i = 0; i < n; i++) {
let l = 0, r = tail.length-1;
while (l <= r) {
const m = l + Math.floor((r-l)/2);
if (tail[m] < nums[i]) {
l = m + 1;
} else {
r = m -1;
}
}
if (l === tail.length) {
tail.push(nums[i]);
} else {
tail[l] = nums[i];
}
}
return tail.length;
};
可视化
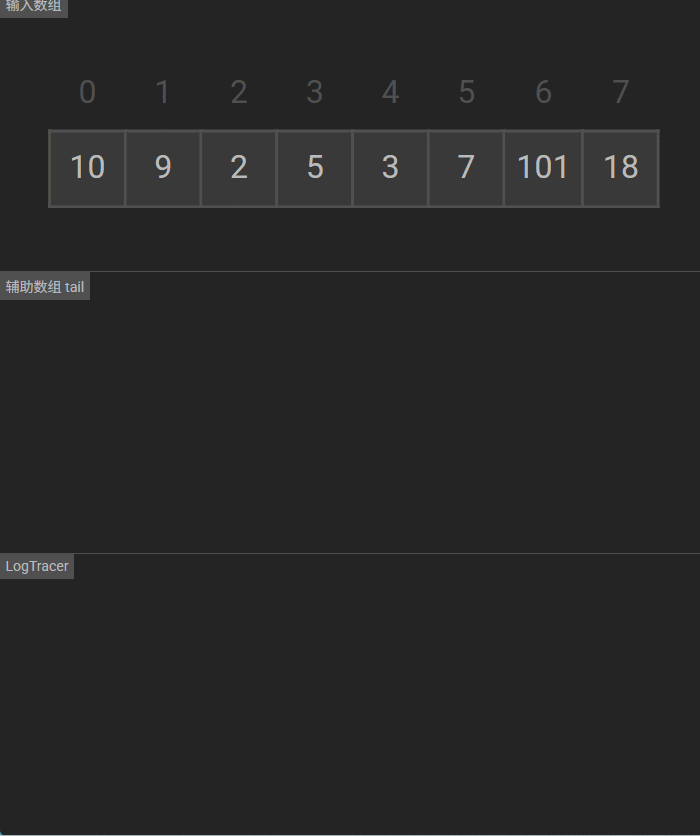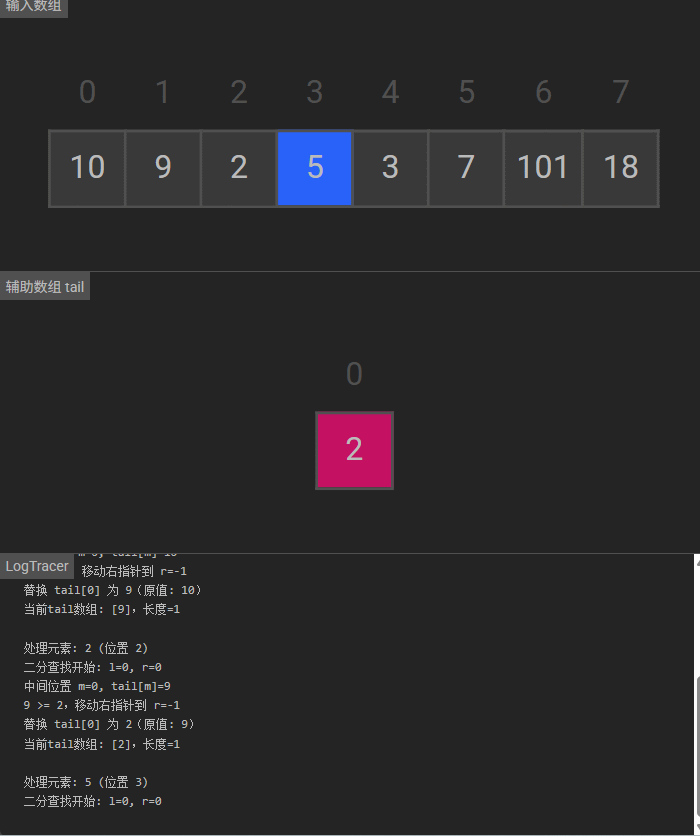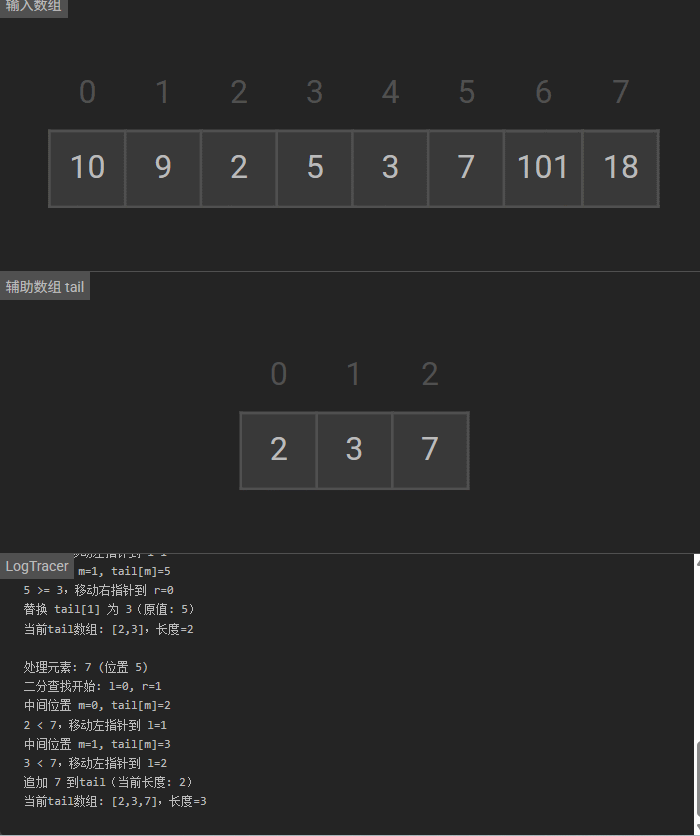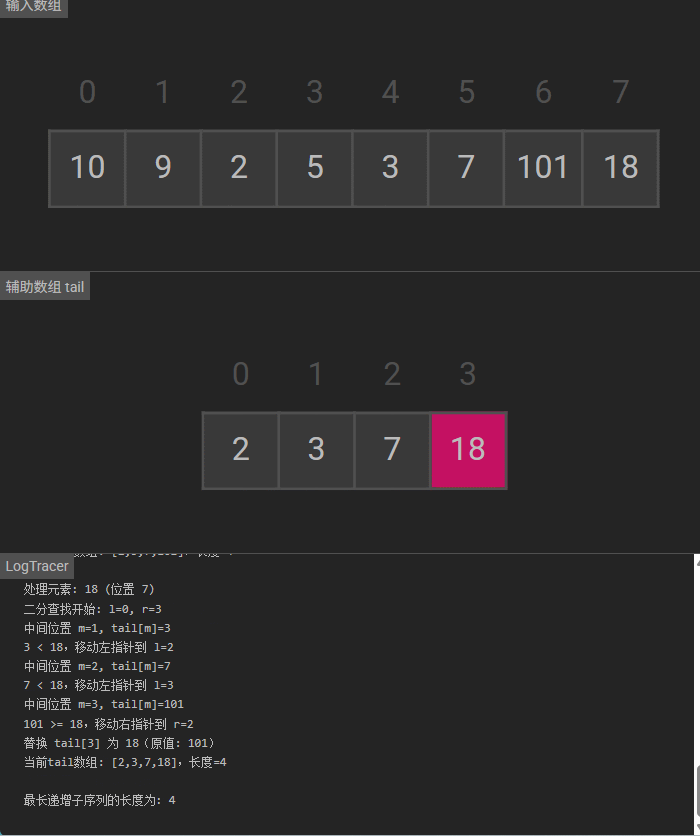






















 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








