【LeetCode热题100道笔记】从前序与中序遍历序列构造二叉树

题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

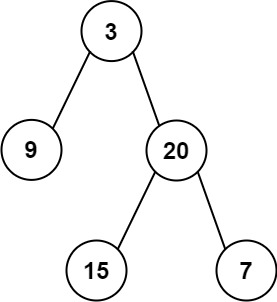
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:
1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列

思考一：原始递归（基于数组切片）

核心是利用前序首元素确定根节点，中序拆分左右子树序列，通过数组切片获取子序列，递归构造左右子树。

算法过程

1. 终止条件：若前序序列为空（preorder.length === 0），说明当前子树为空，返回null。
2. 确定根节点：
   • 前序序列第一个元素preorder[0]即为当前子树的根节点值；
   • 创建根节点root = new TreeNode(rootVal)。
3. 拆分中序序列：
   • 在中序序列中找到根节点值的索引rootIndex（inorder.indexOf(rootVal)）；
   • 中序左子树序列：inorder.slice(0, rootIndex)（根节点左侧元素，均为左子树节点）；
   • 中序右子树序列：inorder.slice(rootIndex + 1)（根节点右侧元素，均为右子树节点）。
4. 拆分前序序列：
   • 前序左子树序列：preorder.slice(1, 1 + rootIndex)（长度与中序左子树一致，从根节点后开始取）；
   • 前序右子树序列：preorder.slice(rootIndex + 1)（剩余元素，长度与中序右子树一致）。
5. 递归构造子树：
   • 根节点的左子树 = 递归调用buildTree（传入前序左子树序列、中序左子树序列）；
   • 根节点的右子树 = 递归调用buildTree（传入前序右子树序列、中序右子树序列）。
6. 返回结果：返回当前根节点，完成递归回溯，最终构建整棵二叉树。

时间复杂度：O(n²)。其中n为节点总数，原因是：

• 每层递归中，indexOf操作需遍历中序序列，耗时O(n)；
• slice操作会创建新数组，耗时O(k)（k为子序列长度），总耗时O(n²)；
• 递归深度为O(n)（最坏情况，链状树），总时间为O(n²)。

空间复杂度：O(n²)。原因是：

• 递归调用栈深度为O(n)；
• 每层递归的slice操作会产生新数组，总空间为O(n²)（所有子序列的长度和）。

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder) {
    if (!preorder.length) return null;
    const rootVal = preorder[0];
    const root = new TreeNode(rootVal);
    const rootIndex = inorder.indexOf(rootVal);
    root.left = buildTree(preorder.slice(1, 1 + rootIndex), inorder.slice(0, rootIndex));
    root.right = buildTree(preorder.slice(rootIndex+1),  inorder.slice(rootIndex+1));
    
    return root;
};

思考二：优化递归（基于索引边界，避免数组切片）

原始递归的slice操作会产生新数组，增加空间开销。优化思路是用索引边界标记子序列范围（而非切片），通过preStart/preEnd（前序子序列边界）和inStart/inEnd（中序子序列边界）定位子序列，减少空间消耗。

算法过程

1. 初始化递归入口：调用辅助函数buildBTree，传入完整序列的索引边界：
   • 前序边界：preStart=0，preEnd=preorder.length（左闭右开区间）；
   • 中序边界：inStart=0，inEnd=inorder.length（左闭右开区间）。
2. 辅助函数终止条件：若preStart >= preEnd（前序子序列为空），返回null。
3. 确定根节点与中序 pivot：
   • 前序子序列首元素preorder[preStart]为当前根节点值，创建根节点root；
   • 遍历中序子序列[inStart, inEnd)，找到根节点值的索引pivot（中序根节点位置）。
4. 计算左子树长度与子序列边界：
   • 左子树长度leftSize = pivot - inStart（中序左子树元素个数）；
   • 左子树边界：
     • 前序左子树：preStart+1（根节点后开始）到preStart+1+leftSize（左子树长度结束）；
     • 中序左子树：inStart到pivot（根节点左侧）；
   • 右子树边界：
     • 前序右子树：preStart+1+leftSize（左子树结束后开始）到preEnd；
     • 中序右子树：pivot+1（根节点右侧）到inEnd。
5. 递归构造子树：
   • 根节点左子树 = 递归buildBTree（传入左子树边界参数）；
   • 根节点右子树 = 递归buildBTree（传入右子树边界参数）。
6. 返回结果：辅助函数返回当前根节点，最终入口函数返回整棵树的根节点。

时间复杂度：O(n²)。其中n为节点总数，原因是：

• 每层递归中，遍历中序子序列找pivot耗时O(n)；
• 递归深度为O(n)（最坏情况，链状树），总时间为O(n²)。
• （优化潜力：若用哈希表存储中序值与索引的映射，可将找pivot的时间降至O(1)，总时间优化为O(n)）。

空间复杂度：O(n)。原因是：

• 递归调用栈深度为O(n)（最坏情况）；
• 无需创建新数组，仅使用原数组和索引变量，额外空间为O(n)。

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder) {
   
    return buildBTree(preorder, inorder, 0, preorder.length, 0, inorder.length);
};

function buildBTree(preorder, inorder, preStart, preEnd, inStart, inEnd) {
    if (preStart >= preEnd) return null;
    const rootVal = preorder[preStart];
    const root = new TreeNode(rootVal);
    let pivot = -1;
    for (let i = inStart; i < inEnd; i++) {
        if (inorder[i] === rootVal) {
            pivot = i;
            break;
        }
    }
    const leftSize = pivot - inStart;
    root.left = buildBTree(preorder, inorder, preStart+1, preStart+1+leftSize, inStart, pivot);
    root.right = buildBTree(preorder, inorder, preStart+1+leftSize, preEnd, pivot+1, inEnd);

    return root;
}