题目描述
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1
输出:[1]
提示:
1 <= nums.length <= 105
-104 <= nums[i] <= 104
1 <= k <= nums.length
思考一(优先队列)
使用最大堆(优先队列)维护滑动窗口中的元素,可高效获取当前窗口的最大值。核心思路如下:
- 堆中存储窗口元素的「值+索引」,确保能判断元素是否仍在窗口内;
- 窗口右移时,将新元素插入堆中;
- 每次取堆顶元素(当前最大值),若其索引已超出窗口范围(小于左边界),则弹出该元素,直至堆顶元素在窗口内;
- 此时堆顶元素即为当前窗口的最大值,记录结果。
该方法的关键是仅移除不在窗口内的最大值,无需处理堆中其他元素(即使它们已出窗口),因为它们不会影响当前及后续窗口的最大值判断。插入元素的时间复杂度为 O(logn)O(\log n)O(logn),每个元素最多被弹出一次,因此整体时间复杂度为 O(nlogn)O(n \log n)O(nlogn)。
算法过程
-
初始化最大堆:
- 自定义
MyMaxPriorityQueue类实现最大堆,堆中元素为[值, 索引]数组(存储元素值及其在原数组中的索引),确保能判断元素是否在当前窗口内。 - 先将数组
nums中前k个元素插入堆中,构建初始滑动窗口。
- 自定义
-
提取初始窗口最大值:
- 堆顶元素即为初始窗口(前
k个元素)的最大值,将其加入结果数组ans。
- 堆顶元素即为初始窗口(前
-
滑动窗口右移并更新:
- 从第
k个元素开始遍历nums,每次将当前元素[nums[i], i]插入堆中(扩展窗口至右侧新元素)。 - 检查堆顶元素(当前最大值)的索引是否在窗口范围内(窗口左边界为
i - k + 1,右边界为i):- 若堆顶元素索引
<= i - k(已超出左边界,不在窗口内),则弹出堆顶元素,重复此过程直至堆顶元素在窗口内。
- 若堆顶元素索引
- 将此时的堆顶元素值(当前窗口最大值)加入
ans。
- 从第
-
返回结果:
- 遍历结束后,
ans中存储了所有滑动窗口的最大值,返回ans。
- 遍历结束后,
核心逻辑:通过最大堆快速获取当前窗口的最大值,仅在堆顶元素超出窗口范围时才移除(无需处理堆中其他无效元素),平衡了插入和删除操作的效率,确保每个元素最多被插入和弹出堆一次。
代码
/**
* @param {number[]} nums
* @param {number} k
* @return {number[]}
*/
var maxSlidingWindow = function(nums, k) {
const queue = new MyMaxPriorityQueue(k);
for (let i = 0; i < k; i++) { // 构建窗口
queue.add([nums[i], i]);
}
const ans = [queue.front()[0]];
for (let i = k; i < nums.length; i++) {
queue.add([nums[i], i]);
while (queue.front()[1] <= i-k) { // 优先队列最大值在窗口外面就移除,其它较小值不用关心是否在窗口内外
queue.pop();
}
ans.push(queue.front()[0]);
}
return ans;
};
class MyMaxPriorityQueue {
constructor() {
this._data = [];
}
front() {
return this._data[0];
}
add(num) {
this._data.push(num);
this.swim();
}
pop() {
if (this._data.length === 0) return;
[this._data[0], this._data[this._data.length-1]] = [this._data[this._data.length-1], this._data[0]];
this._data.pop();
this.sink();
}
swim(index = this._data.length-1) {
while (index > 0) {
let pIndex = Math.floor((index-1)/2);
if (this._data[index][0] > this._data[pIndex][0]) {
[this._data[index], this._data[pIndex]] = [this._data[pIndex], this._data[index]];
index = pIndex;
continue;
}
break;
}
}
sink(index = 0) {
const n = this._data.length;
while (true) {
let left = 2 * index + 1;
let right = left + 1;
let biggest = index;
if (left < n && this._data[left][0] > this._data[index][0]) {
biggest = left;
}
if (right < n && this._data[right][0] > this._data[biggest][0]) {
biggest = right;
}
if (biggest !== index) {
[this._data[biggest], this._data[index]] = [this._data[index], this._data[biggest]];
index = biggest;
continue;
}
break;
}
}
}
思考二(单调队列)
滑动窗口的核心是高效维护窗口内的最大值,单调队列(双端队列)通过保持队列内元素的单调性,可在 O(1)O(1)O(1) 时间获取最大值,整体复杂度优化至 O(n)O(n)O(n)。
核心思路:
- 队列存储元素的索引(而非值),确保能判断元素是否在当前窗口内;
- 队列内元素对应的数值从左到右严格单调递减,因此队首元素即为当前窗口的最大值;
- 窗口右移时,通过“移除窗口外元素”和“剔除无效元素”两步维护队列单调性,保证每次操作后队首始终是窗口最大值。
算法过程
-
初始化队列:
- 用双端队列
dqueue存储元素索引,初始为空;结果数组ans存储每个窗口的最大值。
- 用双端队列
-
遍历数组元素(索引
i从 0 到nums.length-1):-
步骤1:移除窗口外的元素
若队首元素的索引<= i - k(已超出当前窗口左边界i - k + 1),则从队首弹出(shift()),确保队列中仅保留窗口内元素。 -
步骤2:剔除无效元素
从队尾开始,若队列非空且当前元素nums[i]大于队尾索引对应的元素值,则弹出队尾元素(pop())。重复此操作,直至队尾元素值大于等于nums[i]或队列为空。
(目的:维持队列单调性,确保新加入的元素不会被比它小的元素“遮挡”,保证后续窗口的最大值能被正确记录) -
步骤3:加入当前元素
将当前元素的索引i加入队尾,此时队列仍保持单调递减。 -
步骤4:记录最大值
当i >= k - 1(窗口已完全形成),队首元素对应的数值即为当前窗口的最大值,将其加入ans。
-
-
返回结果:
遍历结束后,ans中存储了所有滑动窗口的最大值,返回ans。
关键逻辑:通过“左删(窗口外元素)”和“右剔(小于当前值的元素)”维护队列单调性,使得每次窗口移动后,队首始终是窗口内的最大值,且每个元素仅入队和出队一次,因此时间复杂度为 O(n)O(n)O(n)。
代码
/**
* @param {number[]} nums
* @param {number} k
* @return {number[]}
*/
var maxSlidingWindow = function(nums, k) {
const dqueue = []; // 单调队列,存索引,对应的数值从左到右递减
const ans = [];
for (let i = 0; i < nums.length; i++) {
if (dqueue.length && dqueue[0] <= i-k) { // 移除窗口外的索引
dqueue.shift();
}
while (dqueue.length && nums[i] > nums[dqueue[dqueue.length-1]]) {//队尾小于当前元素的没用,直接丢弃
dqueue.pop();
}
dqueue.push(i);
if (i >= k-1) {
ans.push(nums[dqueue[0]]);
}
}
return ans;
};
可视化
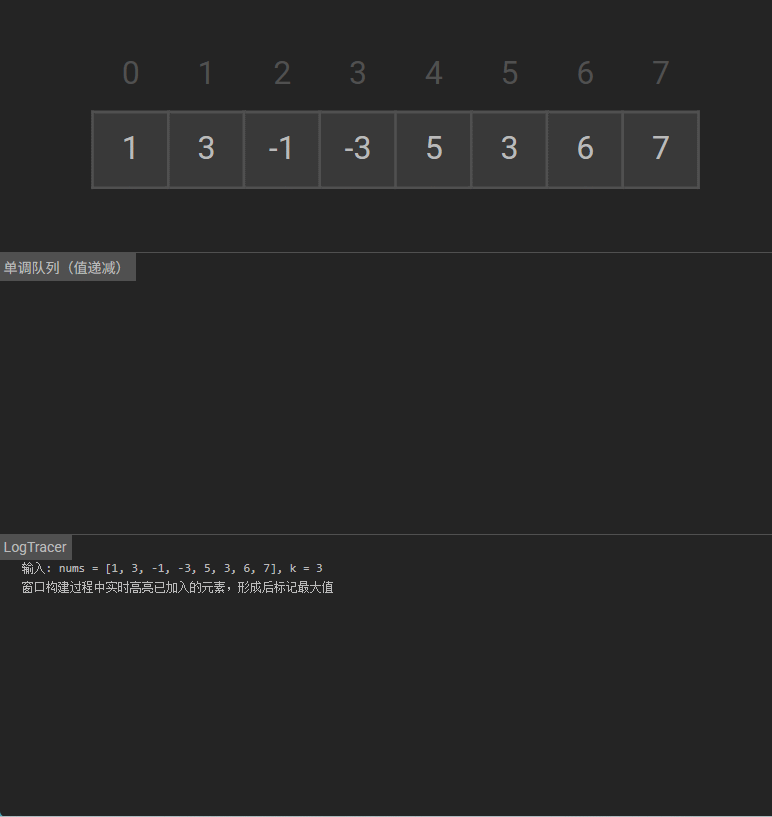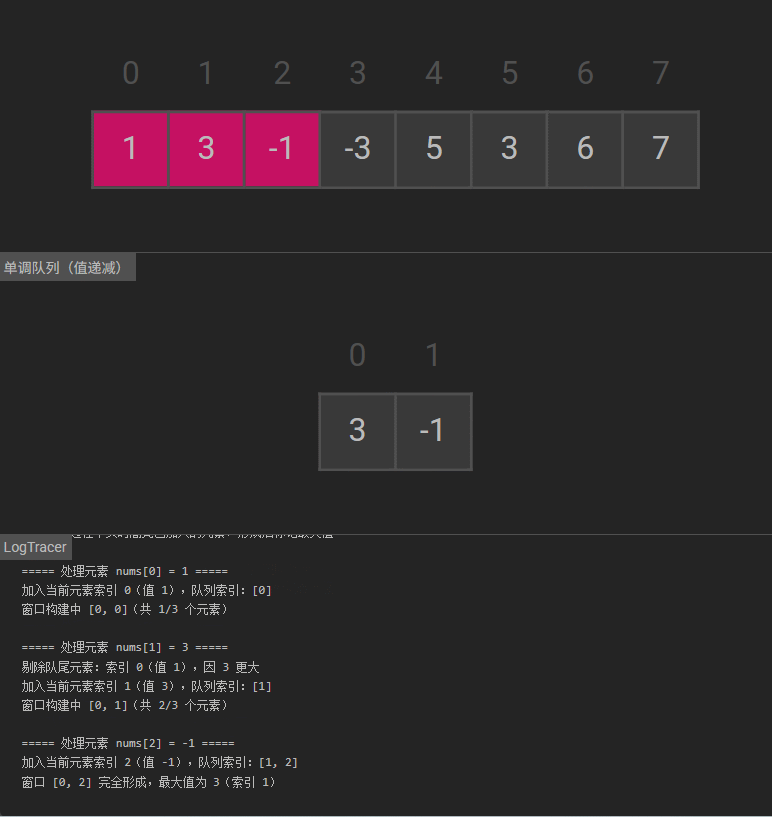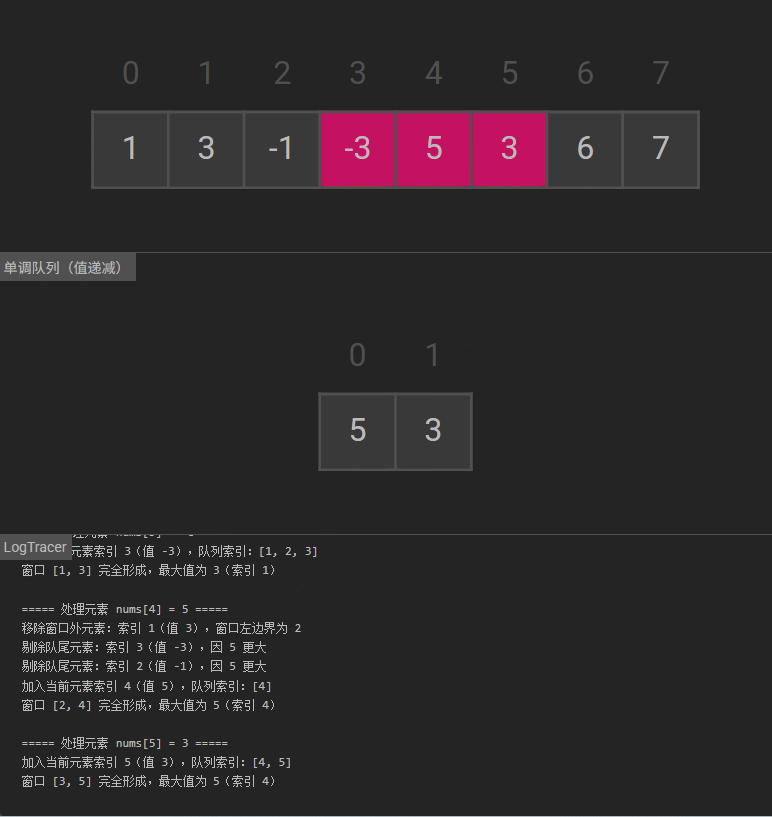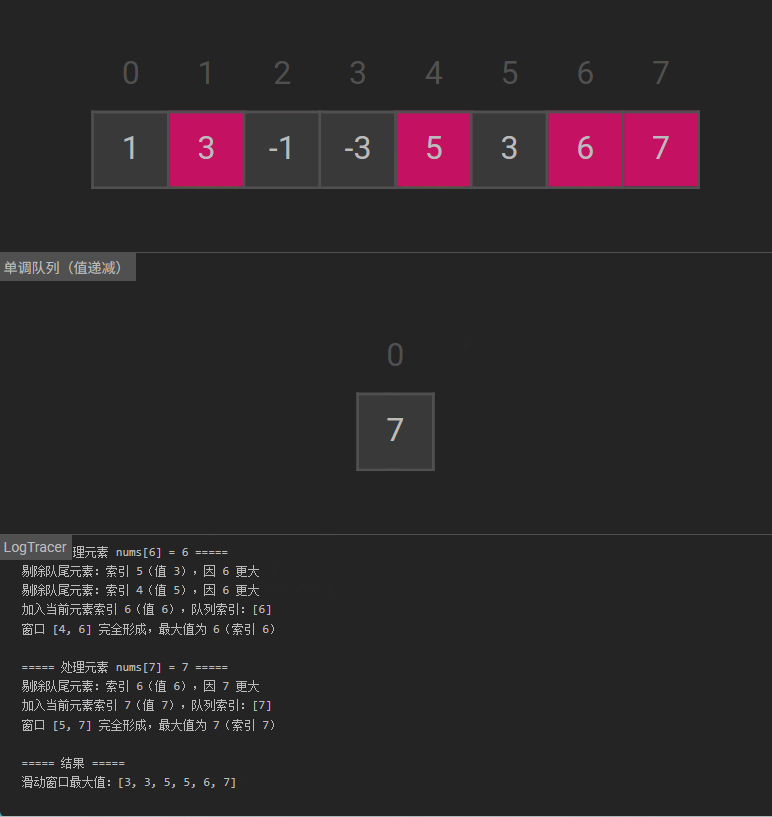





















 889
889

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








