【LeetCode热题100道笔记+动画】找到字符串中所有字母异位词-优快云博客

题目描述

给定两个字符串 s 和 p，找到 s 中所有 p 的异位词的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

示例 1:
输入: s = “cbaebabacd”, p = “abc”
输出: [0,6]
解释:
起始索引等于 0 的子串是 “cba”, 它是 “abc” 的异位词。
起始索引等于 6 的子串是 “bac”, 它是 “abc” 的异位词。

示例 2:
输入: s = “abab”, p = “ab”
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 “ab”, 它是 “ab” 的异位词。
起始索引等于 1 的子串是 “ba”, 它是 “ab” 的异位词。
起始索引等于 2 的子串是 “ab”, 它是 “ab” 的异位词。

提示:
1 <= s.length, p.length <= 3 * 104
s 和 p 仅包含小写字母

思考

寻找字符串 s 中 p 的异位词，核心是找到所有长度与 p 相等且字符计数完全一致的子串。由于字符仅为小写字母，可通过定长滑动窗口结合计数数组高效判断：

用两个长度为26的数组分别记录 p 的字符计数和窗口内的字符计数；
窗口大小固定为 p 的长度，在 s 中滑动时，通过增减边界字符的计数维持窗口状态；
若两计数数组完全一致，则当前窗口为 p 的异位词，记录起始索引。

算法过程

初始化计数数组：
- 计算 p 中每个字符的出现次数，存入 pcodes 数组（索引对应 ‘a’-‘z’，值为计数）；
- 初始化 codes 数组记录窗口内字符计数，初始化为全0。
构建初始窗口：
- 滑动窗口大小固定为 p.length（记为 n），先将 s 中前 n 个字符的计数填入 codes。
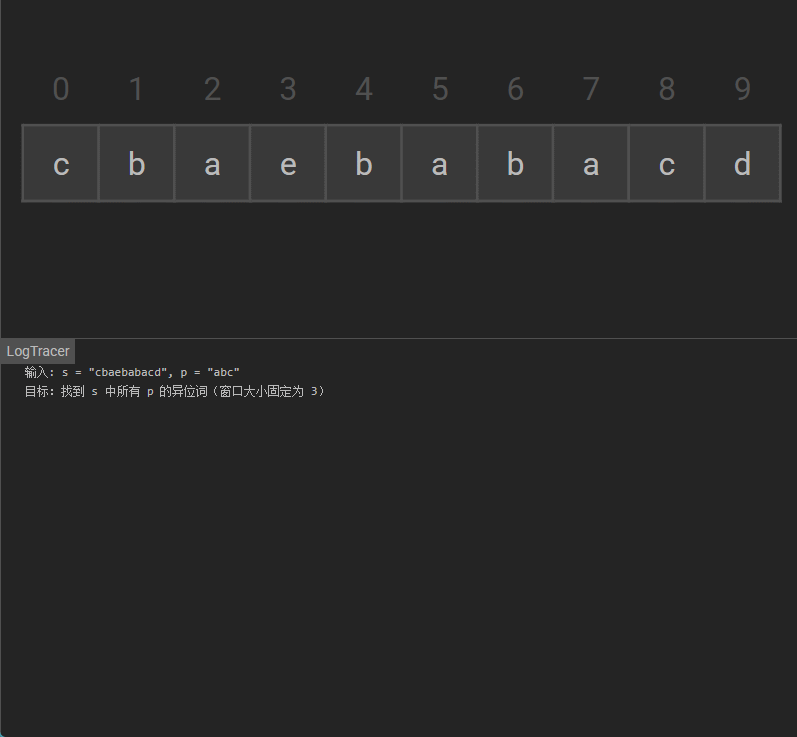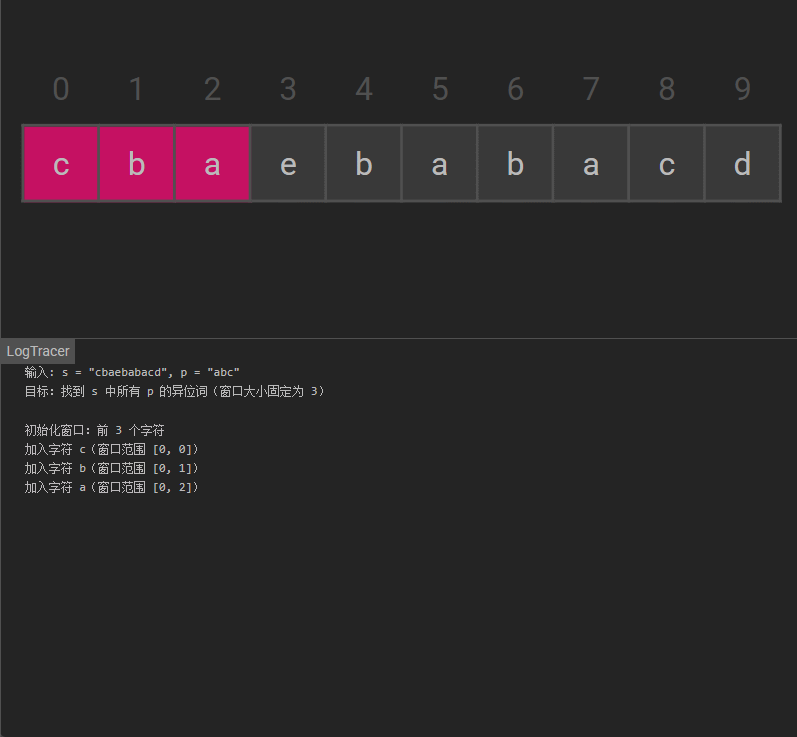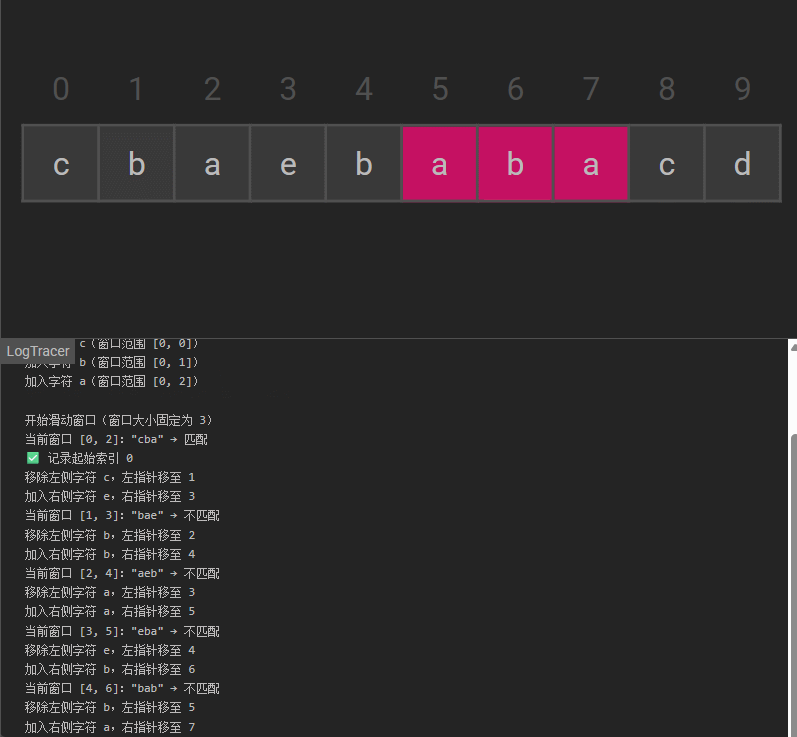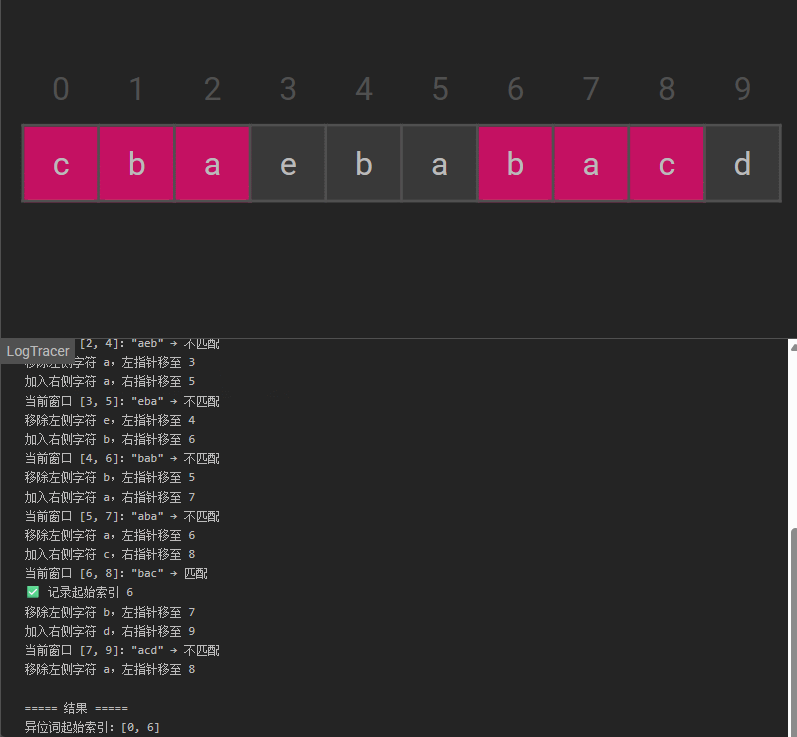
滑动窗口并判断：
- 每次滑动时，先判断当前窗口的 codes 与 pcodes 是否一致，若一致则记录窗口起始索引 l；
- 左指针 l 右移，从 codes 中减去移出窗口的字符计数；
- 右指针 r 右移，向 codes 中加入新进入窗口的字符计数；
- 重复上述步骤，直至 r 遍历完 s。
返回结果：
- 收集所有符合条件的起始索引，返回结果数组。

该方法利用定长窗口避免了频繁调整窗口大小，通过计数数组对比替代字符排序，时间复杂度为 $O (m + n)$ （m 为 s 长度，n 为 p 长度），空间复杂度为 $O (1)$ （仅用两个固定大小的数组）。

代码

/**
 * @param {string} s
 * @param {string} p
 * @return {number[]}
 */
var findAnagrams = function(s, p) {
    const ans = [], n = p.length;
    if (n > s.length) return ans;


    const pcodes = Array(26).fill(0);
    const aCode = 'a'.charCodeAt(0);
    for (let c of p) {
        pcodes[c.charCodeAt(0) - aCode]++;
    }
    const pcodesStr = pcodes.toString();
    const codes = Array(26).fill(0);
    let l = 0, r = 0;
    
    while (r-l+1 <= n) { // 初始化定长窗口
        codes[s[r].charCodeAt(0)-aCode]++;
        r++;
    }
    r--;
    
    while (r < s.length) {                
        if (r-l+1 === n) {
            if (codes.toString() == pcodesStr) {
                ans.push(l);
            }
            codes[s[l].charCodeAt(0)-aCode]--;
            l++;
        }
        r++;
        if (r < s.length) {
            codes[s[r].charCodeAt(0)-aCode]++;
        }
    }
    return ans;
};