【OD机试题解法笔记】 完全二叉树非叶子部分后序遍历

题目

给定一个以顺序储存结构存储整数值的完全二叉树序列（最多 1000 个整数），请找出此完全二叉树的所有非叶子节点部分，然后采用后序遍历方式将此部分树（不包含叶子）输出。
只有一个节点的树，此节点认定为根节点（非叶子）。
此完全二叉树并非满二叉树，可能存在倒数第二层出现叶子或者无右叶子的情况
其他说明：二叉树的后序遍历是基于根来说的，遍历顺序为：左 - 右 - 根

输入描述
一个通过空格分割的整数序列字符串

输出描述
非叶子部分树结构。备注：输出数字以空格分隔

用例

输入	输出	说明
1 2 3 4 5 6 7	2 3 1	找到非叶子部分树结构，然后采用后序遍历输出。

思考

先熟悉完全二叉树：在一棵满二叉树中，在最下层从最右侧起去掉相邻的若干叶子结点，得
到的二叉树即为完全二叉树。

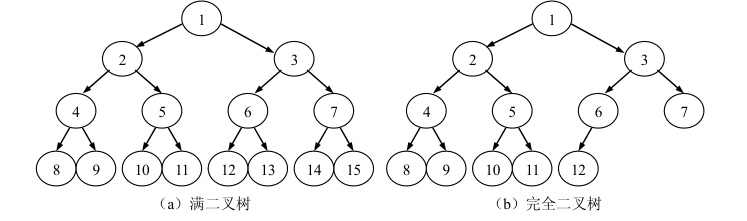
题目要求后序遍历忽略叶子节点，由于后序遍历总是先遍历子节点，只要在遍历每个节点时判断它没有子节点就丢掉，这样最后得到的序列不就是去除叶子节点的树的后序遍历序列。顺序存储的二叉树可以根据每个节点在数组中的索引计算每个节点的左右子节点的位置索引，如果当前节点位置索引是 k， 则其左子节点索引是 2*k + 1, 右子节点是2*k+2。怎么判断某个节点是叶子节点？根据前面的公式计算其左右子节点，如果2*k + 1 > 节点数目N，表示没有左子节点，右子节点同理判断。后序遍历顺序左-右-根，判断是叶子节点直接丢弃回溯且不加入结果列表。

算法过程

1、定义 dfs 函数，接收1个节点索引为参数，从根节点开始遍历 dfs(0)；

2、在 dfs 中先计算当前节点的左子节点索引 left = 2 * i + 1，如果left > 节点总是N，则return，表示是叶子节点，右子节点不用判断了，完全二叉树每一层节点是从左往右排列的，不存在只有右子节点情形；

3、如果左节点不为空，则继续递归搜索左子节点 dfs(left)，随后判断左子节点是否是叶子节点，如果不是加入结果列表中，在前面调用了dfs(left)，所以这里加入结果列表位置刚好在其子节点之后，同理操作右子节点；

4、完成 dfs(0) 遍历，根节点0的子节点都遍历完毕，最后加入根节点，得到最后结果。

参考代码

function solution(line) {
    const tree = line.trim().split(' ');
    let n = tree.length;
    if (n == 1) return tree;

    let result = [];
    let dfs = function(pos) {
        let left = pos * 2 + 1;
        if (left >= n) {
            return;
        }
        dfs(left);
        if (left * 2 + 1 < n) {
            result.push(tree[left]);
        }
        
        if (left + 1 >= n) {         
            return;
        }
        dfs(left+1);
        if ((left + 1) * 2 + 1 < n) {
            result.push(tree[left+1]); 
        }    
    };

    dfs(0);
    result.push(tree[0]);
    
    return result.join(' ');
}


let lines = [
`1 2 3 4 5 6 7`,
`1 2 3 4 5 6`,
`1`,
`1 2`
];

lines.forEach(line => {
    console.log(solution(line));
});