深度学习基本概念

损失函数

loss function，衡量预测值与真实值之间的误差，如平方误差函数square loss。模型训练中，希望找到一组参数，使得训练样本的平均损失最小。

 

优化算法

1）解析解。

2）数值解。小批量随机梯度下降，mini-batch stochastic gradient descent

• 选取⼀组模型参数的初始值，如随机选取；
• 接下来对参数进⾏多次迭代。在每次迭代中，先随机均匀采样⼀个由固定数⽬训练数据样本所组成的小批量（mini-batch）
• 然后求小批量中数据样本的平均损失有关模型参数的导数（梯度）
• 最后⽤此结果与预先设定的⼀个正数的乘积，作为模型参数在本次迭代的减小

 

 

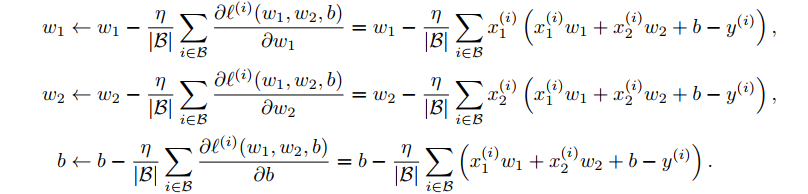
广义线性回归

 

 

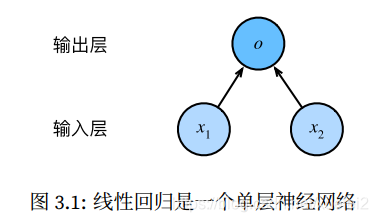
线性回归的神经网络图

线性回归是⼀个单层神经⽹络。输出层中负责计算的单元⼜叫神经元。输出层中的神经元和输⼊层中各个输⼊完全连接。

 

 

 

线性回归从零开始

from IPython import display
from matplotlib import pyplot as plt
from mxnet import autograd, nd
import random

##############################
## 产生数据
##############################
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = nd.random.normal(scale=1, shape=(num_examples, num_inputs))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += nd.random.normal(scale=0.01, shape=labels.shape)
print(features[0], labels[0])

def use_svg_display():
# ⽤⽮量图显⽰
    display.set_matplotlib_formats('svg')

def set_figsize(figsize=(3.5, 2.5)):
    use_svg_display()
    # 设置图的尺⼨
    plt.rcParams['figure.figsize'] = figsize
    
set_figsize()
plt.scatter(features[:, 1].asnumpy(), labels.asnumpy(), 1); # 加分号只显⽰图
plt.show()

##############################
## 读取数据
##############################
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices) # 样本的读取顺序是随机的
    for i in range(0, num_examples, batch_size):
        j = nd.array(indices[i: min(i + batch_size, num_examples)])
        yield features.take(j), labels.take(j) # take函数根据索引返回对应元素。注意，这里使用yield，而不是return

batch_size = 10
for X, y in data_iter(batch_size, features, labels):
    print(X, y)
    break

##############################
## 初始化模型参数
##############################
w = nd.random.normal(scale=0.01, shape=(num_inputs, 1))
b = nd.zeros(shape=(1,))

w.attach_grad()
b.attach_grad()

##############################
## 定义模型
##############################
def linreg(X, w, b): # 本函数已保存在d2lzh包中⽅便以后使⽤
    return nd.dot(X, w) + b

##############################
## 定义损失函数
##############################
def squared_loss(y_hat, y): # 本函数已保存在d2lzh包中⽅便以后使⽤
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

##############################
## 定义优化算法
##############################
def sgd(params, lr, batch_size): # 本函数已保存在d2lzh包中⽅便以后使⽤
    for param in params:
        param[:] = param - lr * param.grad / batch_size

##############################
## 训练模型
##############################
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs): # 训练模型⼀共需要num_epochs个迭代周期
    # 在每⼀个迭代周期中，会使⽤训练数据集中所有样本⼀次（假设样本数能够被批量⼤⼩整除）。 X和y分别是⼩批量样本的特征和标签
    for X, y in data_iter(batch_size, features, labels):
        with autograd.record():
            l = loss(net(X, w, b), y) # l是有关⼩批量X和y的损失
        l.backward() # ⼩批量的损失对模型参数求梯度
        sgd([w, b], lr, batch_size) # 使⽤⼩批量随机梯度下降迭代模型参数
        train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().asnumpy()))

print(true_w, w)
print(true_b, b)

 

线性回归torch实现

########################
## 生成数据集
########################
from mxnet import autograd, nd
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = nd.random.normal(scale=1, shape=(num_examples, num_inputs))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += nd.random.normal(scale=0.01, shape=labels.shape)


########################
## 读取数据集
########################
from mxnet.gluon import data as gdata
batch_size = 10


dataset = gdata.ArrayDataset(features, labels)
# 随机读取⼩批量
data_iter = gdata.DataLoader(dataset, batch_size, shuffle=True)


for X, y in data_iter:
    print(X, y)
    break


########################
## 定义模型
########################
from mxnet.gluon import nn
net = nn.Sequential()
net.add(nn.Dense(1))


########################
## 初始化模型参数
########################
from mxnet import init
net.initialize(init.Normal(sigma=0.01))


########################
## 定义损失函数
########################
from mxnet.gluon import loss as gloss
loss = gloss.L2Loss() # 平⽅损失⼜称L2范数损失


########################
## 定义优化算法
########################
from mxnet import gluon
trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': 0.03})


########################
## 训练模型
########################
num_epochs = 3
for epoch in range(1, num_epochs + 1):
    for X, y in data_iter:
        with autograd.record():
            l = loss(net(X), y)
        l.backward()
        trainer.step(batch_size)
    l = loss(net(features), labels)
    print('epoch %d, loss: %f' % (epoch, l.mean().asnumpy()))


dense = net[0]
print(true_w, dense.weight.data())
print(true_b, dense.bias.data())