深度学习笔记（二）

前言

从线性回归和softmax回归这两种单层神经网络入手，简要介绍机器学习中的基本概念，然后，由单层神经网络延伸到多层神经网络，并通过多层感知机引入深度学习模型。

---

线性回归

基本要素

1.模型
2.模型训练
3.训练数据
4.损失函数，比如平凡函数，交叉熵
5.优化算法,比如小批量随机梯度下降
6.模型预测

线性回归的表示

神经网络图

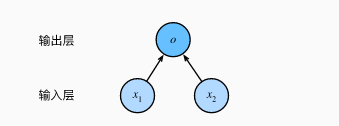
由于输入层并不涉及计数，该神经网络的层数是1。输出层的神经元和输入层中各个输入完全连接。因此，这里的输出层又叫全连接层或稠密层。

矢量计算

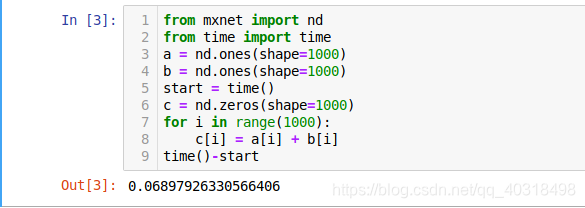
矢量计算比标量计算要快许多，如下是标量加法

如下是矢量加法

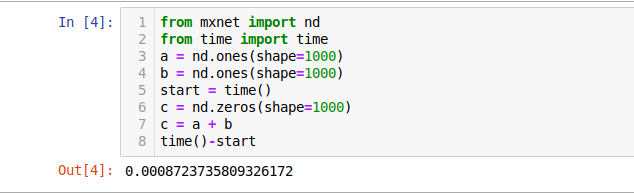
粗略计算了一下，快了大概80倍，因此使用矢量比较省时。

---

线性回归的实现

线性回归方程这里，按y = w1x1 + w2x2 + b来实现，因此我们输入个数（特征数）为2，假设样本数为1000，真实权重为w=[2,−3.4]⊤ 和偏差b = 4.2，下面我们开始生成数据集。方程写成y=Xw+b+ϵ,其中ϵ是噪声（符合均值0，标准差0.01的正态分布）

%matplotlib inline
from IPython import display
from matplotlib import pyplot as plt	#可用于作图
from mxnet import autograd,nd
import random
num_inputs = 2			#输入个数
num_examples = 1000		#样本个数
true_w = [2,-3.4]		#权重
true_b = 4.2			#偏置
features = nd.random.normal(scale=1,shape=(num_examples,num_inputs))
#scale:float概率分布的标准差，对应于分布的宽度，scale越大越矮胖，scale越小，越瘦高
labels = true_w[0]*features[:,0] + true_w[1]*features[:,1] + true_b
#1000个预测值.
#features是1000行1列,那么总的就是1行,1000列,运用到了矩阵运算的广播机制
#labels 是1000行1列的向量(每一列是运算结果)
labels +=nd.random.norman(scale=0.01,shape=labels.shape)
#加上噪声
def use_svg_display():
    #用矢量图显示
    display.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5,2.5)):
    use_svg_display()
    #设置图的尺寸
    plt.rcParams['figure.figsize'] = figsize
set_figsize()
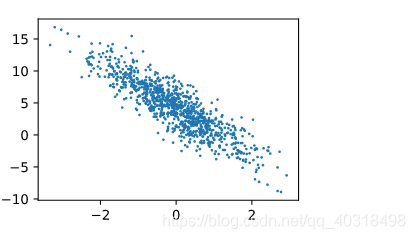
plt.scatter(features[:,1].asnumpy(),labels.asnumpy(),1);
#加分号只显示图,这里画图是x,y的关系
#使用asnumpy可以从NDArray变成Numpy

---

读取数据集

def data_iter(batch_size,features,labels):
    num_examples = len(features)#数据集大小,如1000
    indices = list(range(num_examples))#转换成list形式,如[1,2,3,4,...,num_examples]
    random.shuffle(indices)#样本的读取顺序是随机的,相当于列表打算顺序，每次读取的都不一样
    for i in range(0,num_examples,batch_size):#0-1000，i + batch_size
        j = nd.array(indices[i:min(i+batch_size,num_examples)])#不超出范围...
        yield features.take(j),labels.take(j)#take函数根据索引返回对应元素
        #yield应该是返回结果,take(i)是取features矩阵中的第几行，如j=[0.1.2.]
        #那么对应的就是features中的第0行,1行,2行.labels中的第0行,1行，2行

初始化参数模型

我们将权重初始化成均值为0，标准差为0.01的正态随机数，偏差初始化为0

w = nd.random.normal(scale=0.01,shape=(num_inputs,1))	#权重	
b = nd.zeros(shape=(1,))	#偏差
w.attach_grad()	#对这些参数求梯度来迭代参数的值
b.attach_grad()	#生成梯度需要的内存

定义模型

def linreg(X,w,b):
	return nd.dot(X,w) + b

定义损失函数

def squared_loss(y_hat,y):	#y_hat预测值，y真实值
	return (y_hat - y.reshape(y_hat.shape))**2/2

选用平方函数来衡量价格预测值与真实值之间的误差

定义优化算法

通过不断迭代模型参数来优化损失函数，这里自动求梯度模块来计算得来的梯度是一个批量样本的梯度和，除以样本大小得到平均值。

def sgd(params,lr,batch_size):
	for param in params:
		param[:] = param - lr*param.grad/batch_size #由下面公式得出

在求数值解的优化算法中，小批量随机梯度下降被广泛使用，即先选取一组模型参数的初始值，如随机选取；接下来对参数进行多次迭代，每次迭代都可能降低损失函数值。在每次迭代中，先随机均匀采样一个由固定数目训练数据样本组成的小批量B，然后求小批量中数据样本的平均损失有关模型参数的导数（梯度），如下：

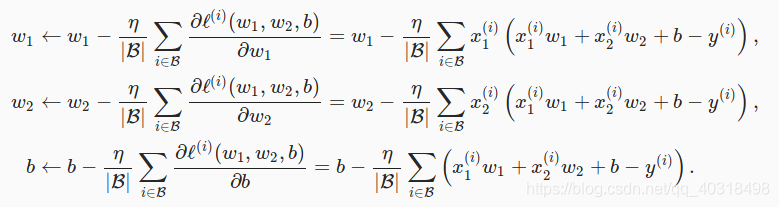
在上式中，|B|代表每个小批量中的样本个数（批量大小，batch size），η称作学习率（learning rate）并取正数。

训练模型

在训练中，我们将多次迭代模型参数。调用反向函数backward计算小批量随机梯度，调用优化算法sgd迭代模型参数,损失l的形状是(10,1)

lr = 0.03 #学习率
num_epochs = 3	#迭代轮数
net = linreg
loss = squared_loss
for epoch in range(num_epochs):
    #训练模型需要num_epochs个迭代周期
    #在每一个迭代周期，会使用训练数据集中所有样本一次
    #X和y分别是小批量样本的特征和标签
    for X,y in data_iter(batch_size,features,labels):
        with autograd.record(): #记录与梯度有关的计算,
            l = loss (net(X,w,b),y) # l是有关小批量X和y的损失
        l.backward() #小批量的损失对模型参数求梯度
        sgd([w,b],lr,batch_size) #使用小批量随机梯度下降迭代模型参数
    train_l = loss (net(features,w,b),labels)
    print ('epoch %d,loss %f' %(epoch+1,train_l.mean().asnumpy()))
    
[out]:
epoch 1,loss 0.028419
epoch 2,loss 0.000100
epoch 3,loss 0.000050

true_w,w #非常接近
([2, -3.4], 
 [[ 1.9998462]
  [-3.3994086]]
 <NDArray 2x1 @cpu(0)>)
 
 true_b,b
 (4.2, 
 [4.19924]
 <NDArray 1 @cpu(0)>)

我们可以通过改变超参数的值，查看不同迭代周期和学习率对模型训练的影响。

---

小结

• 使用Gluon可以更简洁地实现模型
• 在Gluon中，data模块提供了有关数据处理的工具，nn模块定义了大量神经网络的层，loss模块定义各种损失函数
• MXNet的initializer模块提供了模型参数初始化的各种方法。