大模型必知基础知识：1、Transformer架构-QKV自注意力机制

Transformer架构与QKV自注意力机制

原创已于 2025-10-21 16:54:32 修改 · 1.3k 阅读

20 ·

CC 4.0 BY-SA版权

文章标签：

#大模型应用 #qkv #注意力机制 #attention #transformer #人工智能 #大模型实战

于 2025-10-15 07:30:00 首次发布

大模型应用同时被 3 个专栏收录

169 篇文章

订阅专栏

Transformer

33 篇文章

订阅专栏

Embeddings

8 篇文章

订阅专栏

大模型必知基础知识：1、Transformer架构-QKV自注意力机制

总目录

QKV自注意力机制

核心原理

自注意力机制是现代大模型的核心基础，其本质就是计算输入序列中各个Token之间的相关性和重要性。通过Q（查询）与K（键）的交互计算出注意力权重，进而对V（值）进行加权聚合，最终生成融合了上下文信息的输出表示。

在这个机制中，同一个输入序列内的所有词汇会相互计算注意力，形成一个完整的关系网络。最终通过对V矩阵进行加权求和，得到考虑了全局上下文的表示向量。这个值会匹配到词空间矩阵中，找到语义相似的词汇，从而实现语言的理解和生成。

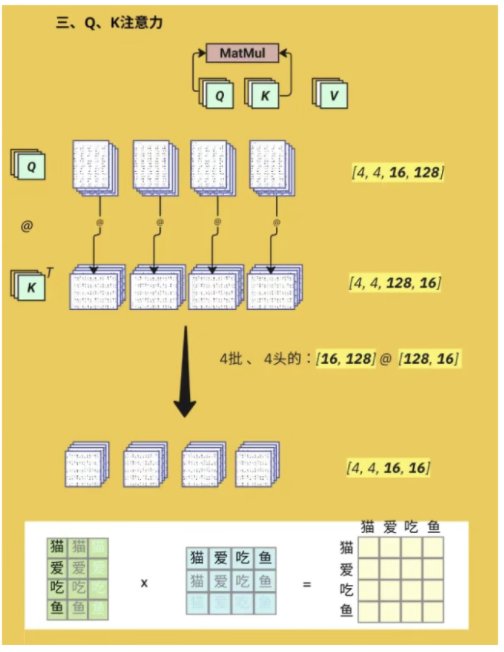
在这里插入图片描述

Q（Query，查询向量）

Q查询向量代表当前要查询的词汇特征，更准确地说，Q是当前输入序列中每个词（或Token）的查询向量表示。

在自注意力机制中，Q并不是只针对单个词进行计算，而是为序列中的所有词同时生成查询向量，这些向量用于主动询问序列中其他词的相关性。通过这种方式，每个词都能获得与整个序列的联系强度。

需要特别强调的是，Q并不等同于"所有已计算过的词汇"。相反，K和Q是一起基于整个输入序列生成的，覆盖序列中的所有词。每个词的Q向量会与所有词（包括自己）的K向量计算相似度，这样才能决定该词应该关注哪些其他词。

K（Key，键向量）

K是所有词的键向量，包括当前词本身。K的作用是为每个词提供一个可被检索的特征表示。

K并不是"所有已计算过的词汇"的累积，而是当前输入序列中每个词的特征表示，用于与Q进行匹配和对比。K和Q都是基于整个输入序列同时生成的，覆盖所有词，这保证了模型能够看到完整的上下文。

K的维度和Q相同，通过学习得到的权重矩阵 $W_K$ 从嵌入向量进行线性变换而来，其形状为[d_k]，其中d_k是键向量的维度。

V（Value，值矩阵）

V矩阵保存的是输入序列中每个词的信息内容。这些内容会在自注意力机制中根据注意力权重被加权聚合，最终生成融合了全序列上下文的表示。

V矩阵的含义

V矩阵的每一行对应一个词的值向量，包含该词的具体语义信息。与Q和K不同，V不直接参与注意力分数的计算阶段。相反，V是作为输出内容的来源存在，只有当注意力权重确定之后，才会根据这些权重对V进行加权求和。

可以这样理解：Q和K决定了"注意什么"，而V决定了"用什么来表达"。这种设计让模型能够灵活地学习既如何分配注意力，又如何表达内容。

V矩阵的生成

V（Value）是从输入序列的嵌入向量（Embedding）通过线性变换生成的向量。具体来说，假设输入序列为X，其形状为[seq_len, d_model]，V矩阵通过权重矩阵 $W_V$ 计算而得：

$\cdot W_V$

其中 $W_V$ 的形状为[d_model, d_v]，d_v是值向量的维度，通常与d_k相同。

V矩阵的生成遵循以下特点：

V矩阵的每一行对应序列中一个词的值向量，包含该词的具体语义信息
V不直接参与注意力分数的计算，而是作为最终加权输出的来源
V通过线性变换生成，使得模型能够学习如何有效地表达内容
Q和K都是基于整个序列生成的，因此K并不是"之前计算过的词汇"，而是当前序列中所有词的表示

自注意力计算过程

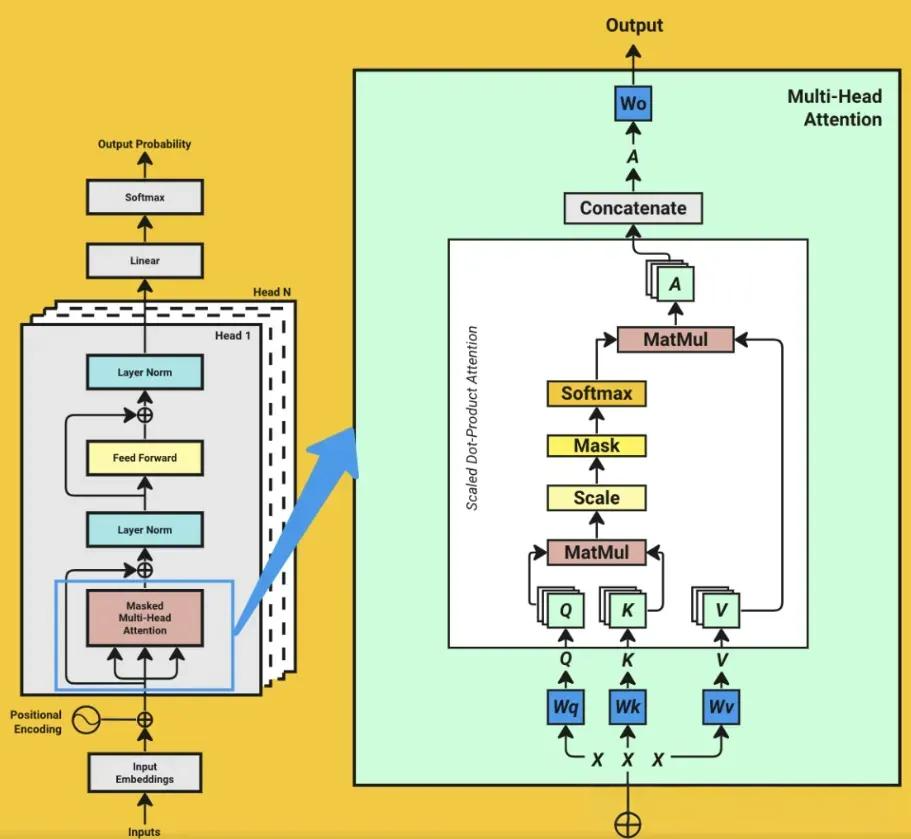
在这里插入图片描述

自注意力机制的计算过程可以分为以下几个步骤：

1. 计算注意力分数

首先计算Q与K的相似度。对于每个查询向量Q，需要与所有的键向量K进行点积运算，计算得到注意力分数：

$\text{Score} = \frac{Q \cdot K^T}{\sqrt{d_k}}$

这里对K进行转置是为了将其从[seq_len, d_k]变换到[d_k, seq_len]，使得矩阵乘法能够进行。分母中的 $\sqrt{d_k}$ 是缩放因子，用于稳定梯度并防止分数过大。

假设分数矩阵的某个元素值为[0.1, 0.2, 0.5, 0.2]，这表示当前词对四个位置的注意力分布（在softmax之前的原始分数）。
在这里插入图片描述

2. 应用Softmax归一化

将注意力分数通过Softmax函数进行归一化，得到注意力权重：

$\text{Attention Weight} = \text{Softmax}(\text{Score})$

例如，对分数[0.1, 0.2, 0.5, 0.2]应用Softmax，可能得到权重[0.15, 0.20, 0.45, 0.20]。这些权重都是正数且求和为1，表示当前词对每个位置的关注程度。
在这里插入图片描述

3. 加权聚合V矩阵

用归一化后的注意力权重对V矩阵进行加权求和：

$\text{Output} = \text{Attention Weight} \cdot V$

例如，若权重为[0.15, 0.20, 0.45, 0.20]，则输出为：

$\text{Output} = 0.15 \cdot V_1 + 0.20 \cdot V_2 + 0.45 \cdot V_3 + 0.20 \cdot V_4$

这个最终输出融合了"我"、“爱”、“吃”、“苹果"四个词的语义信息，权重集中在"吃"和"苹果”，说明当前词最关注这两个关键词汇。

多头注意力机制

实际的Transformer模型中使用了多头注意力机制。多头注意力通过并行计算多个注意力头，每个头学习不同的表示子空间，从而获得更丰富的表达能力。

具体流程为：

将输入序列分别投影到多个不同的Q、K、V空间
在每个头上并行计算自注意力
将多个头的输出连接（Concatenate）起来
通过一个最终的线性变换，得到多头注意力的输出

这种多头设计使得模型能够同时关注序列中的多个不同方面，显著提升了对复杂语义关系的建模能力。

下一个Token的预测过程

整体流程

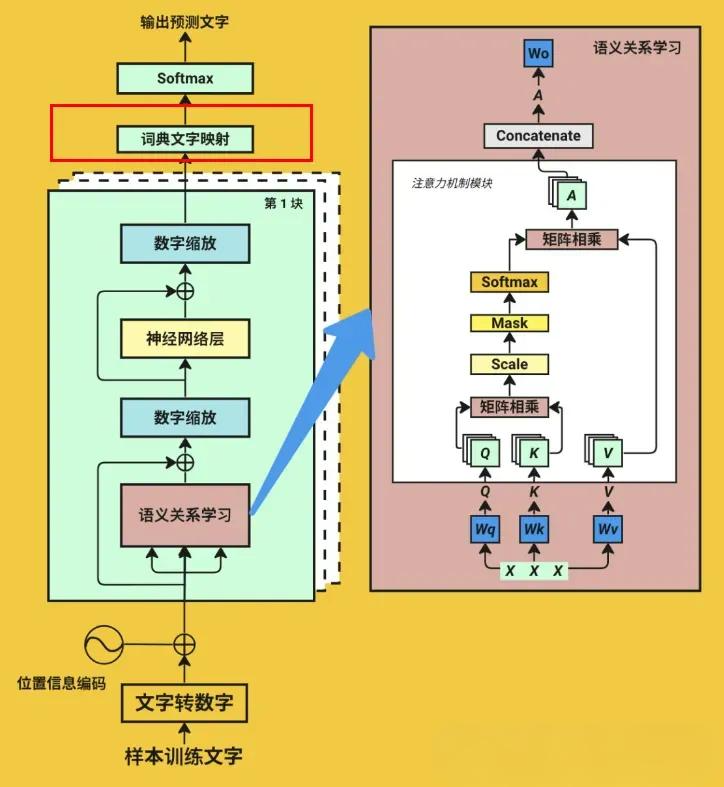
在这里插入图片描述

经过QKV自注意力计算后，模型得到了输入序列经过注意力权重加权后的表示。但这只是一个中间步骤，真正生成下一个Token还需要多个步骤的处理。

具体的预测过程如下：

通过注意力层处理：输入序列通过自注意力机制，得到融合了全局上下文的表示
通过前馈网络处理：经过一个或多个Feed Forward层（全连接网络），对特征进行非线性变换
输出层映射：将处理后的表示通过线性层投影到词表维度，得到每个词在词表中的得分
概率计算：使用Softmax函数将这些得分转换为概率分布
采样或贪心选择：从这个概率分布中选择最可能的Token作为预测结果

简化计算示例

假设使用一个简化的模型来演示整个过程，设词表大小d_k = 2，词表包含四个词汇：[“苹果”、“很”、“好吃”、“甜”]。
在这里插入图片描述

编码阶段（输入端）

编码器处理输入序列：

输入序列的嵌入表示 $H_{enc}$ ：[h_苹果, h_很, h_好吃, h_甜]，每行维度为[1, 2]
通过权重矩阵计算：
- $K_{enc} = H_{enc} \cdot W_K$
- $V_{enc} = H_{enc} \cdot W_V$

解码阶段（输出端）

初始输入和Q计算：

输入特殊Token：（句子开始标记）
生成 $Q_{<BOS>}$ 的值范围为[0.1, 0.2]

计算注意力得分：

计算 $Q_{<BOS>} \cdot K_{enc}^T$ ，假设得分为[0.1, 0.1, 0.3, 0.5]

Softmax权重归一化：

权重分布为[0.15, 0.15, 0.25, 0.45]

输出计算：

输出为：0.15 · V_苹果 + 0.15 · V_很 + 0.25 · V_好吃 + 0.45 · V_甜

预测结果：

通过输出层获得概率：P(苹果) = 0.8，选择"苹果"作为预测词汇

迭代生成：

将"苹果"作为下一个Token输入，重复上述过程继续生成后续Token

反向传播与优化

梯度下降基础

梯度（Gradient）是一个重要的数学概念。简单来说，梯度就是损失函数对模型参数的偏导数。需要区分两个概念：导数是对一个变量求导，而偏导数是对多个变量求导。

在深度学习中，我们通常处理多参数的情况，因此使用偏导数来描述损失函数如何随着每个参数的变化而变化。

反向传播原理

反向传播是训练深度学习模型的核心算法。它的基本思想很简单：根据计算得到的梯度，用学习率乘以梯度得到的值来更新每一层的权重参数。

以一个简单的线性模型为例来说明：

模型设定

假设有一个简单的线性模型： $y = w x + b$

模型参数为权重w和偏置b。

损失函数为均方误差：
$\frac{1}{2}(y_{pred} - y_{true})^2$

梯度计算

对w的偏导数：
$\frac{\partial L}{\partial w} = \frac{\partial L}{\partial y_{pred}} \cdot \frac{\partial y_{pred}}{\partial w} = (y_{pred} - y_{true}) \cdot x$

对b的偏导数：
$\frac{\partial L}{\partial b} = \frac{\partial L}{\partial y_{pred}} \cdot \frac{\partial y_{pred}}{\partial b} = (y_{pred} - y_{true})$

梯度解释

$\frac{\partial L}{\partial w}$ 的值取决于输入x和预测误差：如果x很大，或者预测误差很大，说明对损失的影响更显著，需要对w进行较大的调整
$\frac{\partial L}{\partial b}$ 仅与误差相关：与输入x无关，只取决于预测的准确程度

参数更新

使用梯度信息更新参数：

$w_{new} = w_{old} - \alpha \cdot \frac{\partial L}{\partial w}$

$b_{new} = b_{old} - \alpha \cdot \frac{\partial L}{\partial b}$

其中α是学习率，控制每次更新的步长。学习率的选择至关重要：

学习率过大会导致发散或震荡，模型无法收敛
学习率过小会导致收敛速度过慢，训练效率低下

大模型中的反向传播

在大模型（如Transformer）中，反向传播的原理相同，但应用于数百万甚至数十亿参数。多层网络的梯度通过链式法则逐层传播：

首先计算输出层的梯度
然后逐层向后传播梯度
每一层都会根据接收到的梯度计算该层参数的梯度
最后使用这些梯度通过优化器（如Adam、SGD等）更新参数

这样的过程虽然计算复杂，但原理本质上与简单线性模型的反向传播完全相同。正是这个优雅的数学框架支撑了现代深度学习模型的训练。

总结

QKV自注意力机制、Token预测过程和反向传播优化构成了大模型的三个基础支柱。理解这些概念对于深入学习大模型的原理、进行模型优化调试以及创新算法设计都至关重要。

从注意力权重的计算，到多层次的特征融合，再到通过梯度下降不断优化参数，这整个流程体现了深度学习的核心思想：通过数据驱动的学习过程，让模型逐步提升对复杂模式的理解和生成能力。