杜教筛

最新推荐文章于 2020-12-23 21:58:29 发布

All_fade_away

最新推荐文章于 2020-12-23 21:58:29 发布

阅读量578

点赞数

CC 4.0 BY-SA版权

分类专栏：数学-杜教筛文章标签：数学-杜教筛

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/xmr_pursue_dreams/article/details/86763535

数学-杜教筛专栏收录该内容

2 篇文章

订阅专栏

杜教筛

1.概述

杜教筛是用以解决积性函数前缀和的算法。

在学习了莫比乌斯反演之后，杜教筛的过程就会显得简单而自然。

2.基本形式

对于积性函数 $f$ ，我们定义如下函数：

$S(x)=\sum_{i=1}^{x}f(i)$

构造积性函数 $h,g$ ，使得 $f*g=h$

显然：

$\sum_{i=1}^{n}h(i)=\sum_{i=1}^{n}(f*g)(i)$

进一步转化：

$\sum_{i=1}^{n}h(i)=\sum_{d=1}^{n}g(d)\cdot \sum_{i=1}^{\left \lfloor \frac{n}{d} \right \rfloor}f(i)$

也就是：

$\sum_{i=1}^{n}h(i)=\sum_{d=1}^{n}g(d)\cdot S(\left \lfloor \frac{n}{d} \right \rfloor)$

把右式的第一项提出：

$\sum_{i=1}^{n}h(i)=g(1)S(n)+\sum_{d=2}^{n}g(d)\cdot S(\left \lfloor \frac{n}{d} \right \rfloor)$

进一步整理，得：

$g(1)S(n)=\sum_{i=1}^{n}h(i)-\sum_{d=2}^{n}g(d)\cdot S(\left \lfloor \frac{n}{d} \right \rfloor)$

显然，如果我们能够快速算出任意的 $h(i)$ ，就能够通过数论分块在 $O(n^{\frac{2}{3}})$ 的时间内求出 $S$ 。

3.一些常见函数的杜教筛形式

3.1 $\mu$ 函数的前缀和

有一个显而易见的结论： $\mu*I=\epsilon$

设 $S(n)=\sum_{i=1}^{n}\mu(i)$

由杜教筛易得：

$S(n)=1-\sum_{d=2}^{n}S(\left \lfloor \frac{n}{d} \right \rfloor)$

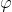3.2 $\varphi$ 函数的前缀和

有一个显而易见的结论： $\varphi*I=id$

设 $S(n)=\sum_{i=1}^{n}\varphi(i)$

由杜教筛易得：

$S(n)=\frac{n(n-1)}{2}-\sum_{d=2}^{n}S(\left \lfloor \frac{n}{d} \right \rfloor)$

4.一些总结

杜教筛作为一个数论算法，代码实现不算太难，但有几个小细节需要注意：

$S(i)$ 是需要全部记录的，需要用到unordered_map或者 map（多一个log）。
实测unordered_map、map，时间差不多
容易爆long long

平时遇到积性函数求和，并且 $n$ 高达 $10^9,10^{10},10^{11}$ ，就可以尝试用杜教筛来解。

当然杜教筛有一个弊端：没有一个系统的构造函数的方法。

如果遇到一个难以构造的积性函数，可以尝试使用 $min$ _ $25$ 筛、洲阁筛，(啥？你不会，我也不会qwq），那自求多福吧（QAQ~)。

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。