Unity 与 UE4 双引擎版本四叉树的创建与可视化

心之凌儿

已于 2022-02-08 17:11:56 修改

阅读量3.5k

点赞数 5

分类专栏： Unity UE 文章标签： unity ue4 游戏引擎四叉树虚幻

于 2022-02-08 15:48:06 首次发布

本文链接：https://blog.youkuaiyun.com/xinzhilinger/article/details/122635033

版权

本文介绍了如何在Unity和UE4中创建四叉树，探讨了四叉树在游戏引擎中的应用，以及四叉树在处理复杂场景时的优缺点。通过提供GitHub项目地址，详细展示了在Unity中创建四叉树的Node和Tree脚本，以及在UE4中的相应实现，同时提到了UE4中的一些编程技巧和差异。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在这里插入图片描述

这次与以往不同的是，会以Unity版本为基础，扩展出UE4的四叉树工程版本

了解四叉树

四叉树作为一种树状数据结构，有很好的区域划分的特点，在局部刷新或状态判断上有广泛的应用，在复杂场景中可以通过分支剔除快速的卸载或添加区域性的数据

在百度百科的描述中写到，四叉树是在二维图片中定位像素的唯一适合的算法。因为二维空间（图经常被描述的方式）中，平面像素可以重复的被分为四部分，树的深度由图片、计算机内存和图形的复杂度决定

因此，作为唯一一种高效的空间索引算法，在游戏引擎的基础加载算法中有大量的应用。

四叉树的应用：

对于复杂场景来说，为了既保证游戏性能又不丢失场景细节，往往会对资源做一些层级处理，比如模型的LOD和贴图的MipMap等技术。

而对于一个大世界最基本的地形处理，就比单一的小模型来的复杂一些，除了区块性的加载地图之外，也有一些技术是对于区块本地的网格处理技术，比如Unity中Terrain网格的曲面细分技术，大概原理是根据相机距离地形的渲染距离不同来设置地形网格的三角面的复杂度，但是一张地形网格太大了，如果所有的区域都设置为相同的复杂度，同样也会造成很大的性能浪费，所以一张网格地图的内部会再一次执行区域划分的操作，划分的策略就是基于四叉树或八叉树为基本数据结构来划分区域：

在这里插入图片描述

但是需要注意的一点是，Unity中Terrain曲面细分的策略的复杂性除了与相机的距离之外，也同样与地形的高度有关。这很好理解，当网格在Y轴上拉伸，网格单位平面内的总面积就会变大，这时如果不提升该区域曲面细分的深度，渲染精度就达不到预期的效果。在Terrain某一区域与相机渲染的距离及该区域的地形高度两者会综合权重得到曲线细分的处理值，表现为四叉树或者八叉树在该区域节点的深度值。但是这种处理同样也会产生一些问题，如图：

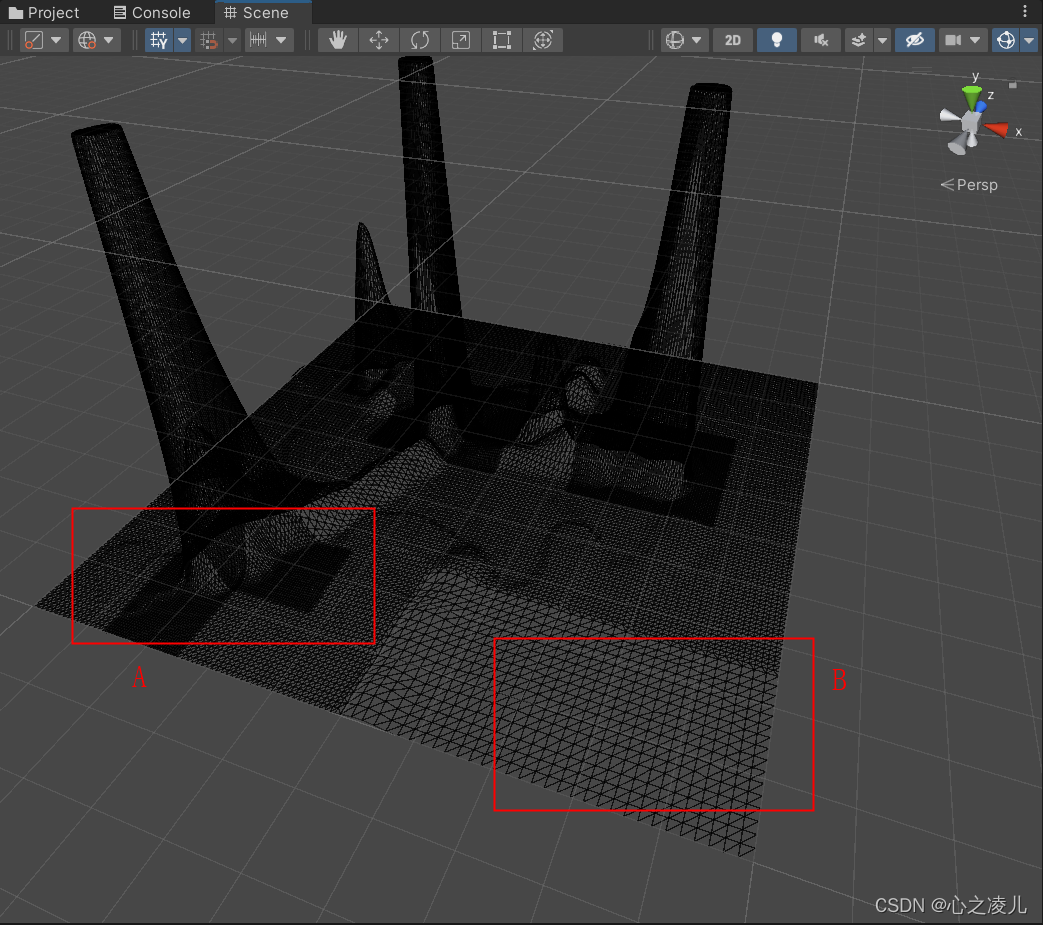
在这里插入图片描述
在上图中，由于受到高度的影响，A区域的部分平坦地图虽然相比于B区域距离相机更远，但是精度却比B区域更远，这也是四叉树带来的负面效应，以分支结果为主题，绑定性强，如下面这张图，当一个区域的高度提升时，该区域对应的四叉树的深度也会增加，相应的其同一分支的节点深度也伴随增加，然后就会不可避免的提升了曲面细分的精度。但是从好的方向考虑的话，这一处理策略也使得Terrain在地形网格变化上有一定连续性

在这里插入图片描述

通过Unity创建四叉树：

项目代码GitHub地址：Unity-QTree

Node脚本：

首先需要通过创建一个Node脚本来实现节点的功能，代码开始前做一些准备工作描述

使用Bounds来做空间界定

四叉树的空间划分，本质就是一个立方体的结构，所以我们依托于Unity中Bounds做结点空间界定，其本身就是一个AABB盒子，也可以直接通过结构体来构造这个Bounds，但是Unity这边直接提供了集成好的代码，所以我们这边直接使用即可

定义初始变量，通过构造函数初始化：

 	public Bounds bound;
    public int layer;
    public Tree belongTree;
    public Node nodeFather;
    public Node[] childList;
    public List<ObjData> objList;

    public Node(Bounds bound,int layer,Tree belongTree,Node nodeFather=null)
    {
   
        this.bound = bound;
        this.layer = layer;
        this.belongTree = belongTree;
        this.nodeFather=nodeFather;
    }

对于节点执行操作时，首先就是子节点的创建，实现也很简单，只需要对父节点做平面四等分分割并确定子节点的Bounds，然后将对应的参数传入即可，子节点Bounds的计算过程如下：

center：父节点center在X轴方向与Z轴方向分别作size的四分之一偏移，不同的偏移方向对应不同子节点的center
size：父节点size的二分之一

将上面的描述转换为代码，结构为：

	public void CreateChildNode()
    {
   
        childList=new Node[4];
        int index = 0;
        for (int i = -1; i <= 1; i+=2)
        {
   
            for (int j = -1; j <= 1; j+=2)
            {
   
                Vector3 centerOffset = new Vector3(bound.size.x / 4 * i, 0, bound.size.z / 4 * j);
                Vector3 cSize = new Vector3(bound.size.x / 2, bound.size.y, bound.size.z / 2);
                Bounds cBound = new Bounds(bound.center + centerOffset, cSize);
                childList[index++] = new Node(cBound, layer + 1, belongTree,this);
            }
        }
    }

数据的插入，会根据节点当前状态做出对应反应：

当节点第一次插入数据时，将数据存储至ObjList。该节点再次执行插入操作时，就需要判断当前节点深度是否达到最大，如果该节点深度达到最大，同样直接将数据存储到ObjList。如果该节点深度没有最大，需要判断当前节点的子节点是否创建，未创建就创建子节点。存在子节点后就可以对子节点执行遍历，获取到数据所属的子节点区域，然后将数据插入到该子节点内，执行一个递归的操作：

	public void Insert(ObjData obj)
    {
   
        if (objList == nul

最低0.47元/天解锁文章