梦熊NOIP十三联测 C题 两棵树

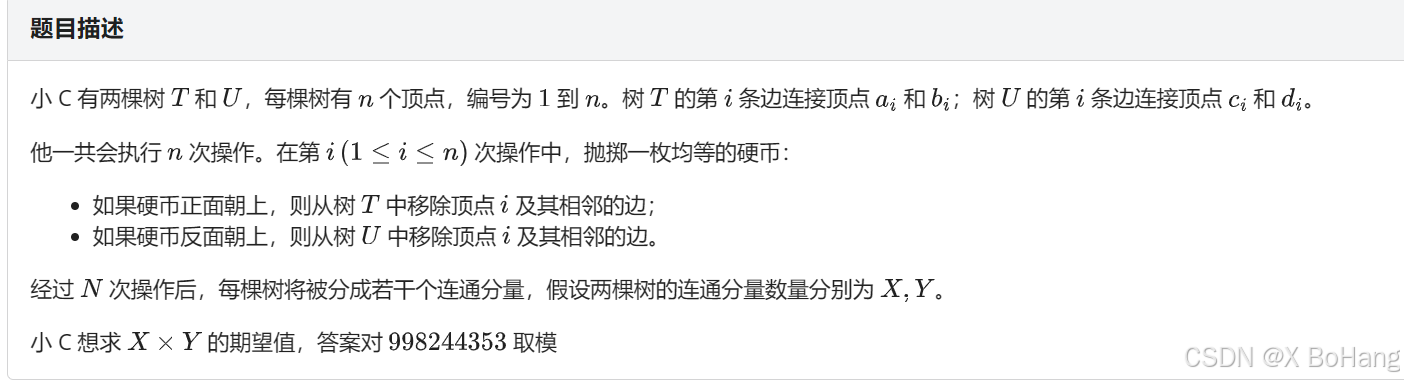
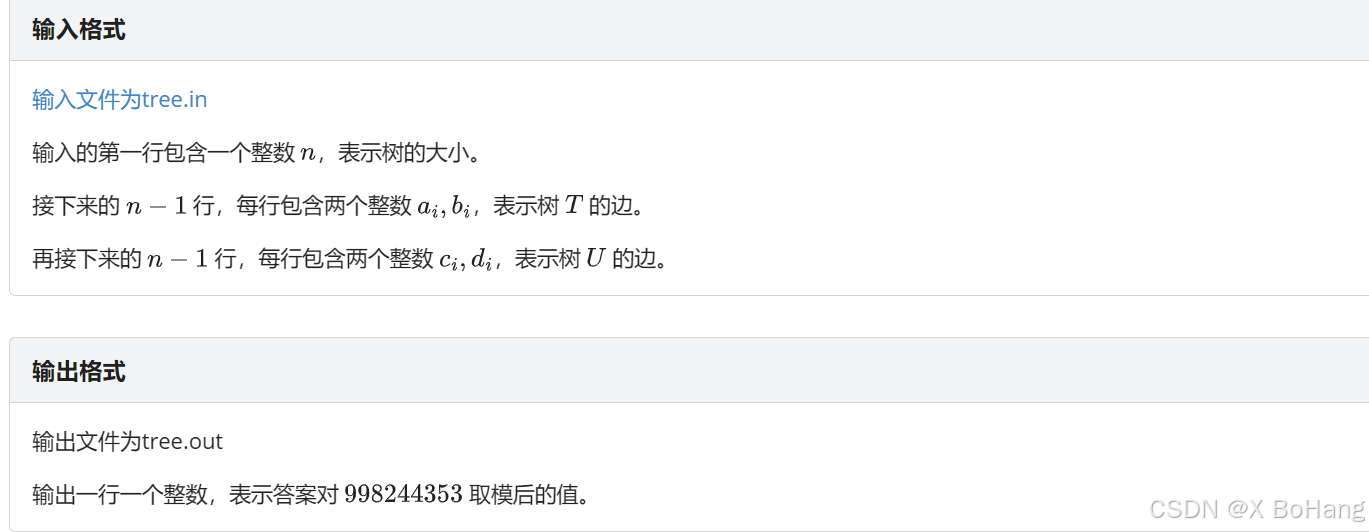
解题思路：

首先做这道题之前我们要知道的基本知识：连通块数=剩余点数-剩余边数（对于此题而言）

我们所要求的贡献，被拆成了4个部分：点*点-边*点-点*边+边*边

我们先以边*边为例，对于树T的边（u，v）假设它被保留（概率为1/4），那么树U中u，v必定被删除。计算树U中有多少条边（x，y）不以u或v为端点。计算每条边（x，y）都有1/4的概率被保留。

可以用set维护每个结点的边，时间复杂度为O(n logn)

这道题也是有部分分的，我在比赛时思路想得挺正确，没想到WA了一个点，不是，今天再看怎么AC了，看来是测评机出了问题。

AC代码如下：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pll;
const int mod = 998244353;
const int MAXN = 200011;
set<ll> a[MAXN], b[MAXN];
ll fac[MAXN], inv[MAXN];
ll n;
ll read() {
    ll x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar();
    return x * f;
}
ll max(ll a, ll b) { return a > b ? a : b; }
ll min(ll a, ll b) { return a < b ? a : b; }
void umax(ll &a, ll t) {
    if (t > a)
        a = t;
}
void umin(ll &a, ll t) {
    if (t < a)
        a = t;
}
ll Qpow(ll a, ll p = mod - 2) {
    if (p < 0)
        return 0;
    ll res = 1;
    while (p) {
        if (p & 1)
            res = res * a % mod;
        a = a * a % mod;
        p >>= 1;
    }
    return res;
}
void add(ll &x, ll y) { x = (x + y) % mod; }
ll C(ll n, ll m) { return n < m ? 0 : fac[n] * inv[m] % mod * inv[n - m] % mod; }
int main() {
    freopen("tree.in", "r", stdin);
    freopen("tree.out", "w", stdout);
    n = read();
    if (n == 1)
        return puts("0"), 0;
    fac[0] = 1;
    inv[0] = 1;
    for (ll i = 1; i <= n; i++) {
        fac[i] = fac[i - 1] * i % mod;
        inv[i] = Qpow(fac[i]);
    }
    for (ll i = 1; i < n; i++) {
        ll u = read(), v = read();
        a[u].insert(v), a[v].insert(u);
    }
    for (ll i = 1; i < n; i++) {
        ll u = read(), v = read();
        b[u].insert(v), b[v].insert(u);
    }
    ll ans = 0;
    for (ll i = 1; i <= n; i++) {
        add(ans, C(n, i) * i % mod * (n - i));
        add(ans, 2 * (mod - (C(n - 2, i) * i % mod * (n - 1) % mod)));
    }
    ll ctrb = (n < 4 ? 0 : Qpow(2, n - 4));
    for (ll u = 1; u <= n; u++) {
        for (auto v : a[u]) {
            if (u > v)
                continue;
            add(ans, ctrb * (n - 1 - b[u].size() - b[v].size() + b[u].count(v)) % mod);
        }
    }
    for (ll i = 1; i <= n; i++) {
        ans = ans * inv[2] % mod;
    }
    printf("%lld\n", ans);
    return 0;
}

暴力打了一下，只会过前几个点，后面的会WA，但也能拿到30分

#include <bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;

const int MAXN = 200001, MOD = 998244353;

int n, u, v, f[MAXN], sz[MAXN], ans;
vector<pii> e, g;

int getfa(int u) { return (f[u] == u ? u : f[u] = getfa(f[u])); }

void Merge(int u, int v) {
    u = getfa(u), v = getfa(v);
    if (u != v) {
        if (sz[u] > sz[v]) {
            swap(u, v);
        }
        f[u] = v, sz[v] += sz[u];
    }
}

int Pow(int a, int b) {
    int ret = 1;
    for (; b; a = 1ll * a * a % MOD, b >>= 1) {
        if (b & 1) {
            ret = 1ll * ret * a % MOD;
        }
    }
    return ret;
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    freopen("tree.in", "r", stdin);
    freopen("tree.out", "w", stdout);
    cin >> n;
    for (int i = 1, u, v; i < n; ++i) {
        cin >> u >> v;
        e.emplace_back(u, v);
    }
    for (int i = 1, u, v; i < n; ++i) {
        cin >> u >> v;
        g.emplace_back(u, v);
    }
    for (int i = 0; i < (1 << n); ++i) {
        iota(f + 1, f + n + 1, 1);
        fill(sz + 1, sz + n + 1, 1);
        int x = 0, y = 0;
        for (auto [u, v] : e) {
            if (!((i >> (u - 1)) & 1) && !((i >> (v - 1)) & 1)) {
                Merge(u, v);
            }
        }
        for (int j = 1; j <= n; ++j) {
            x += (!((i >> (j - 1)) & 1) && f[j] == j);
        }
        iota(f + 1, f + n + 1, 1);
        fill(sz + 1, sz + n + 1, 1);
        for (auto [u, v] : g) {
            if (((i >> (u - 1)) & 1) && ((i >> (v - 1)) & 1)) {
                Merge(u, v);
            }
        }
        for (int j = 1; j <= n; ++j) {
            y += (((i >> (j - 1)) & 1) && f[j] == j);
        }
        ans = (ans + 1ll * x * y % MOD) % MOD;
    }
    cout << 1ll * ans * Pow((1 << n) % MOD, MOD - 2) % MOD;
    return 0;
}