Matlab 定点仿真 ----- 限幅 | 相关运算

1、本限幅方法将得到的整数定点转回便于与原始数据的小数定点

%%限幅%%
        rxFilterOut_real = real(rxFilterOut);
        rxFilterOut_imag = imag(rxFilterOut);
        rxFilterOut_real(rxFilterOut_real.*2^(AI.l-4)>=2^(AI.l-1))=(2^(AI.l-1)-1)./2^(AI.l-4);
        rxFilterOut_real(rxFilterOut_real.*2^(AI.l-4)<=-2^(AI.l-1))=-(2^(AI.l-1)-1)./2^(AI.l-4);
        rxFilterOut_imag(rxFilterOut_imag.*2^(AI.l-4)>=2^(AI.l-1))=(2^(AI.l-1)-1)./2^(AI.l-4);
        rxFilterOut_imag(rxFilterOut_imag.*2^(AI.l-4)<=-2^(AI.l-1))=-(2^(AI.l-1)-1)./2^(AI.l-4);
        rxFilterOut = rxFilterOut_real+1j*rxFilterOut_imag;

1、其中AI.l表示定点位数；
2、其中使用的数字4为符号位与小数位需要的位数；
3、本方法将幅度限制为定点位数可以表示的最大值。

2、定点相关运算

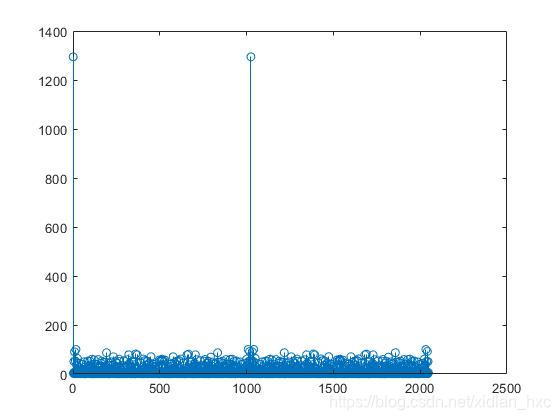
• 定点相关运算确定定时位置一般使用定门限的方法，该门限为了满足所有可能出现的情况一般会使得粗定时（这里表搜索接收帧数据中两段相同的训练符号作相关运算峰值）定时性能较差，而粗定时相关运算的运算量较小（只是在一个时钟加减FIFO中进出的一个值），细定时运算量较大，这样就使得细定时（接收序列与本地序列相关，每个时钟都需要完全重新运算）压力加大，为了减小运算压力，可以将本地训练序列实部虚部只保留符号位，原始数据为0的则保持不表，这样可以大大减小细定时运算量（需要验证原始序列与只保留符号位的序列的相关性，性能过差则不可使用）。
• 实例相关性验证
  
• Matlab 源码

%% 主函数
chu_1024 = chu(1024);
repmat_chu_3 = repmat(chu_1024,1,3);
real_chu_1024 = real(chu_1024);
imag_chu_1024 = imag(chu_1024);

sign_real_chu_1024 = zeros(1,1024);
index_real = find(real_chu_1024 ~= 0);
sign_real_chu_1024(index_real) = real_chu_1024(index_real)./abs(real_chu_1024(index_real));

sign_imag_chu_1024 = zeros(1,1024);
index_imag = find(imag_chu_1024 ~= 0);
sign_imag_chu_1024(index_imag) = imag_chu_1024(index_imag)./abs(imag_chu_1024(index_imag));

sign_chu_1024 = sign_real_chu_1024 + 1i*sign_imag_chu_1024;

inter = zeros(1,1024*2-1);
for i = 1 : 1024*2-1
    inter(i) = sum(repmat_chu_3(i:i+1024-1).*conj(sign_chu_1024));
end
stem(abs(inter))

%% chu序列生成函数
function UW=chu(U)
for n = 0:U-1
        F(n+1) = (pi*n*n)./U;
end
I = cos(F);
Q = sin(F);
UW = I + 1i*Q;
end

参考：用matlab产生chu序列和frank序列

微信公众号：通信随笔XIDIAN