从多项式乘法到快速傅里叶变换

原创已于 2025-11-19 10:43:38 修改 · 1.4k 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #人工智能 #机器学习

于 2025-11-18 22:51:25 首次发布

一般来说，要想理解快速傅里叶变换需要非常多的前置知识，因此，本文希望通过大家都熟悉的多项式乘法来对快速傅里叶变换的设计思路进行讲解，从而让大家能更好的理解这个算法。

前置：了解线代中的范德蒙矩阵和求逆矩阵

多项式乘法

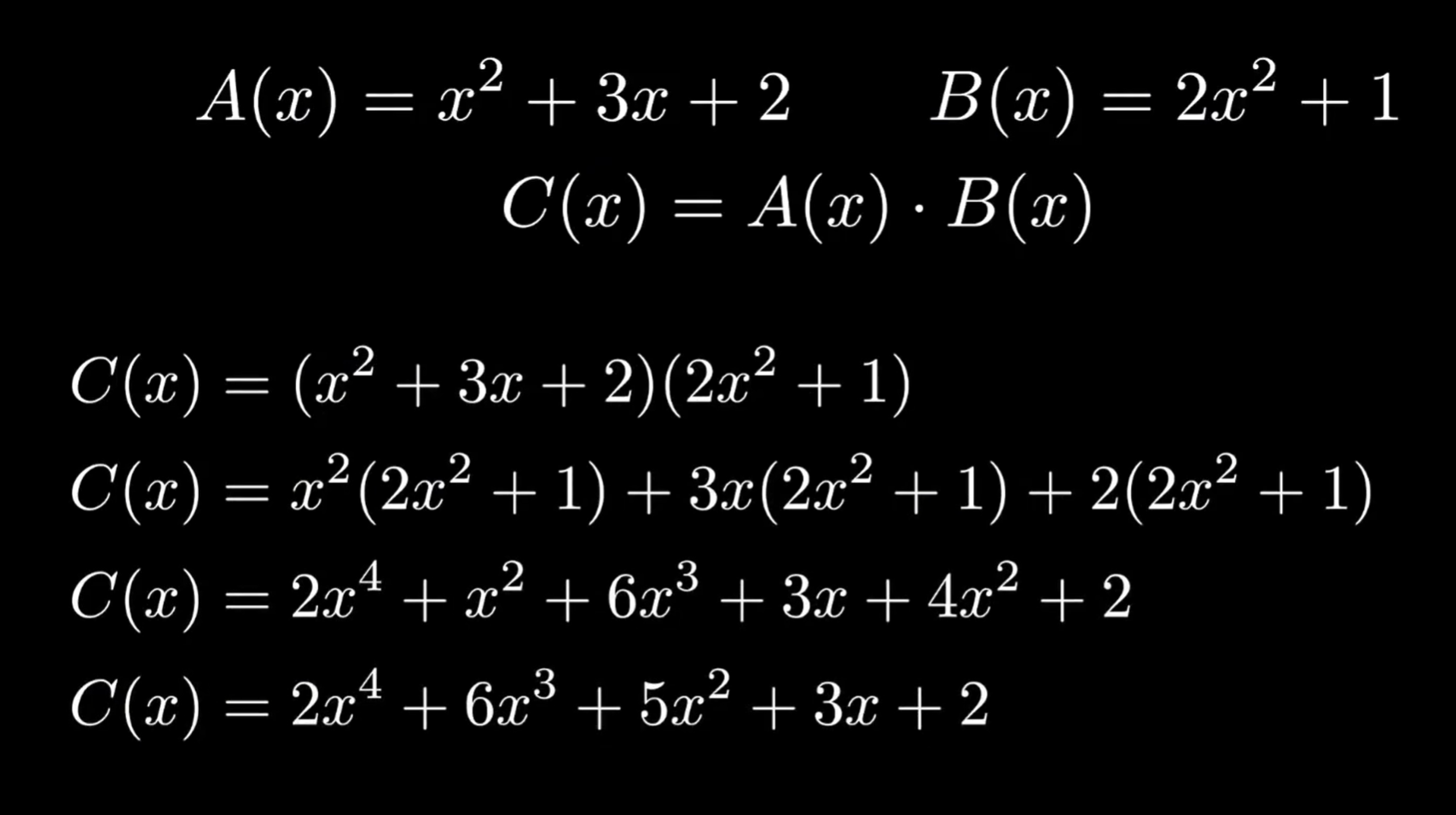
首先来看到我们最常用的计算多项式的方式——乘法分配律，应该不需要多介绍什么，我们直接来看这种方法的问题，假如 $A(x)$ 、 $B(x)$ 都是一个n次多项式，那么乘法分配律的时间复杂度就变成了 $O(n^2)$ ，能不能设计一种更为高效的算法呢？

多项式的表示方法

1、系数表示法

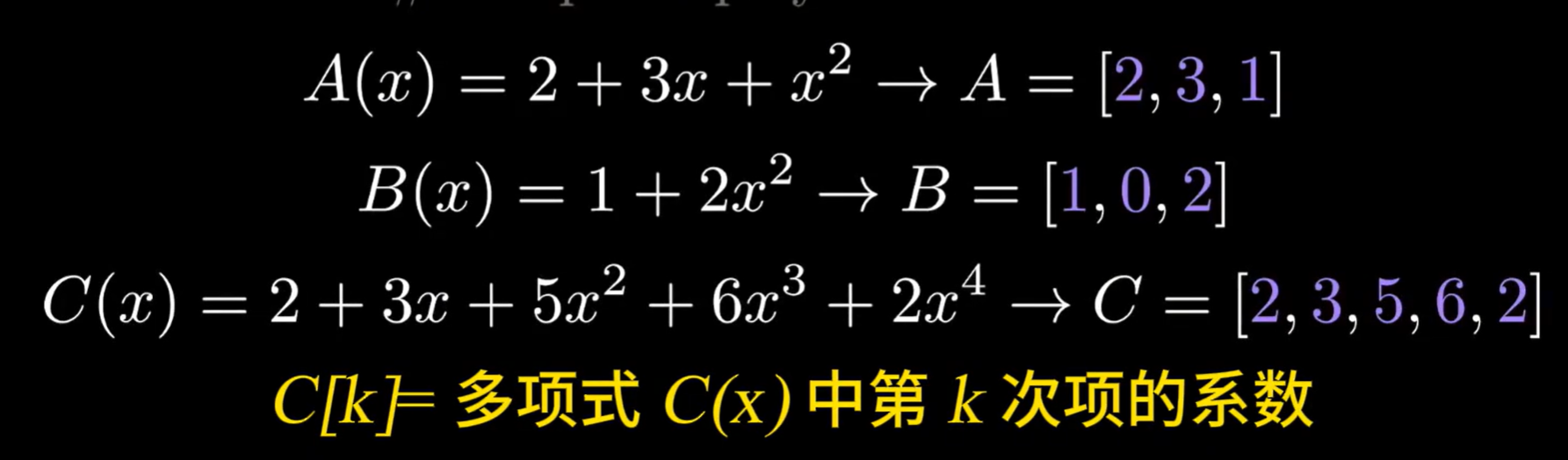
即上述的最常用的表示方法，在代码实现上，我们可以使用列表来完成多项式系数的记录，这种方式下对应的多项式乘法如我们之前所说的，不够高效。

2、值表示法

值表示法的核心理论是：d+1个点可以唯一确定一个d次多项式，例如要确定一个两次多项式（抛物线），只需要找到三个点就可以唯一确定这个二次多项式。也就是说，如果我们给定了三个点的横纵坐标，那么我们总是能为二次多项式找到了一组唯一的系数，使这三个点都在抛物线上。

证明如下：

一个 d 次多项式的一般形式是 $P(x) = p_0 + p_1x + p_2x^2 + \dots + p_dx^d$ ，其中有 $d+1$ 个未知系数 $p_0 , p_1 , p_2 , \dots , p_d$ 。

要确定这 $d+1$ 个系数，需要建立 $d+1$ 个独立的方程。而 “d+1 个点 $(x_0,y_0), (x_1,y_1), \dots, (x_d,y_d)$ ” 恰好能提供 $d+1$ 个方程： $\begin{cases} y_0 = p_0 + p_1x_0 + p_2x_0^2 + \dots + p_dx_0^d \\ y_1 = p_0 + p_1x_1 + p_2x_1^2 + \dots + p_dx_1^d \\ \vdots \\ y_d = p_0 + p_1x_d + p_2x_d^2 + \dots + p_dx_d^d \end{cases}$

将其写为矩阵表达：

其中系数矩阵实际上是一个范德蒙矩阵，由于我们保证了x取值各不相同，因此对应的行列式一定不为0，从而就说明了这个方程组只有唯一解。也就证明了d+1个点可以唯一确定一个d次多项式。

值表示法如何计算多项式乘法呢？

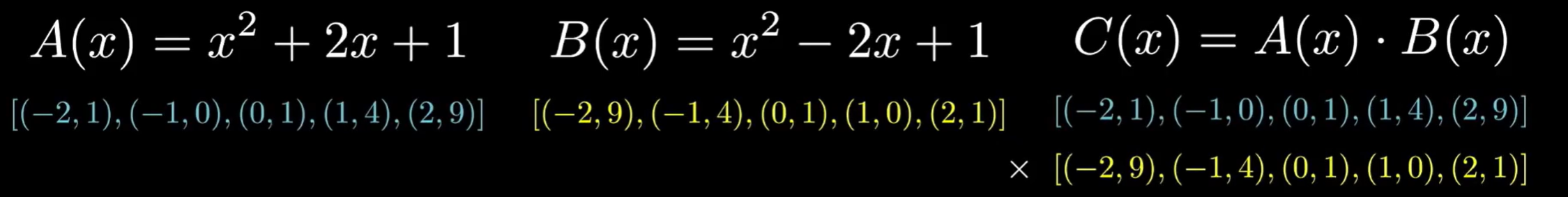
如图所示： $C(x)$ 应当是一个四次多项式，因此需要五个点来确定它的系数，我们在 $A(x)$ 、 $B(x)$ 中找出对应的五个点算出值，再将值相乘，这样就找到了五个点，这样原本n^2的乘法次数似乎是被降低到了k*n次（k为常数），这是一个巨大的提升。

因此，我们将这种算法总结如下：

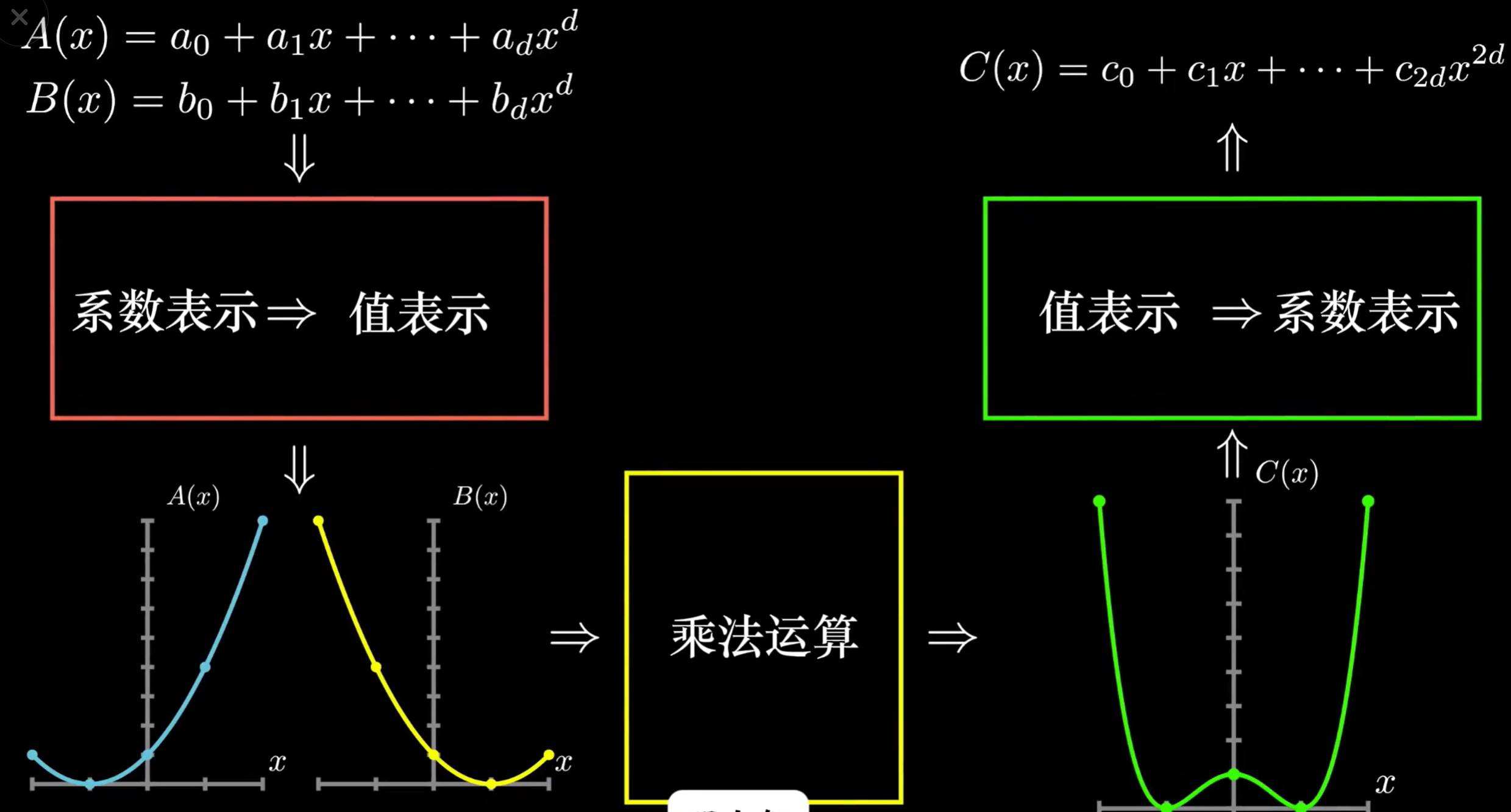
首先将在已知多项式中找出对应点求值，再将值进行乘法得到所求多项式的值表示，最后再将值表示转换为系数表示。这里，将系数表示转换值表示的过程，就是快速傅里叶变换算法；将值表示转换为系数表示的过程，就是逆快速傅里叶变换算法。

值表示法的问题

我们实际上在代值计算的过程容易发现，虽然n和d是无关的两个变量，但当其规模都很大时，这种新的计算多项式乘法又退化到了n^2（原因在于对于每个点求对应值的时候，都需要带入多项式中进行乘法计算，如果有n个点需要带入求值，而多项式本身又是d阶的，当d接近n之后，就会退化；当n<<d或d<<n时，不会退化），能不能优化一下呢？

例如，我们需要求解 $y=kx^2$ ，这里我想要找八个点来进行值表示（理论上来说3个点就足够了，这里八个点是为了后续讲解方便）

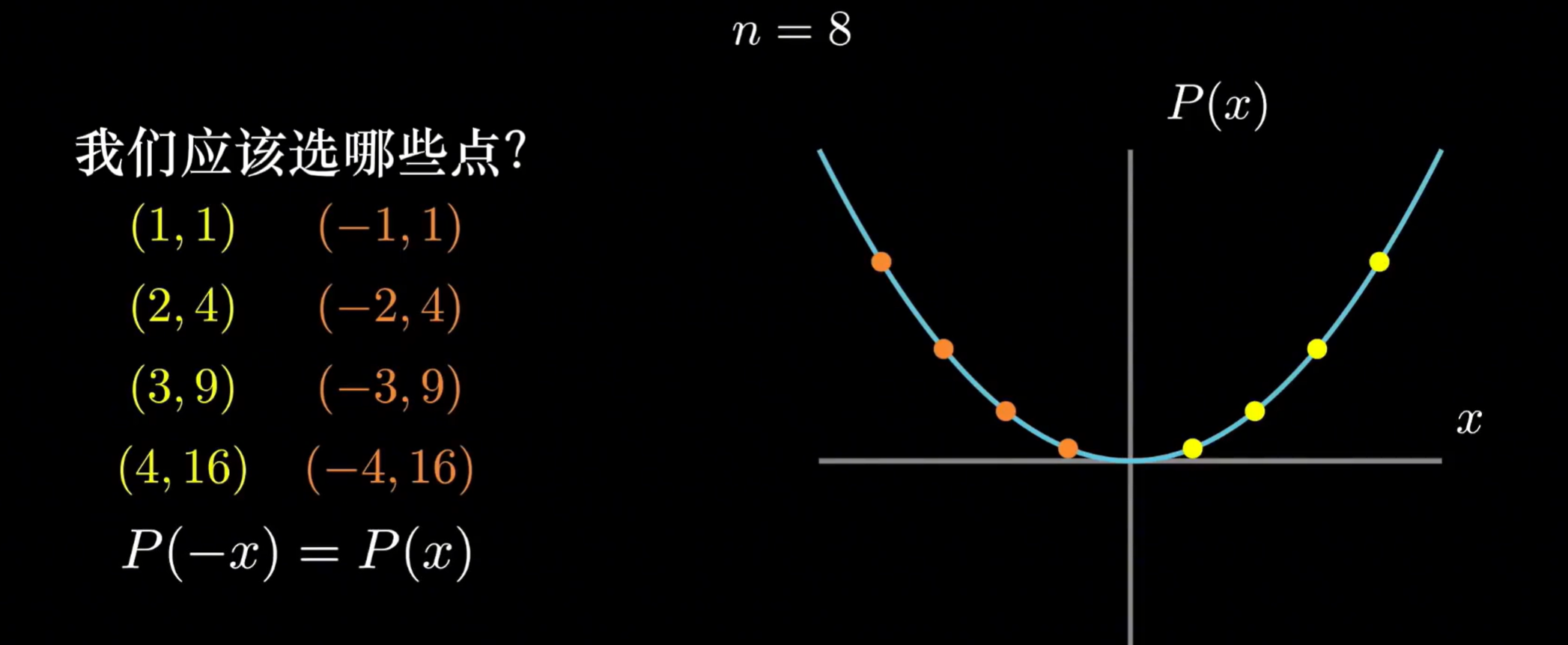
对于 $y=kx^2$ ，我们可以选择一些对称的点，当我们知道x=1处y的取值，不需要计算我们就可以知道x=-1处y的取值，看似需要八个点，实际上我们只计算了四个点。

同样的，对于 $y=kx^3$ ，找八个点也可以有类似的方法

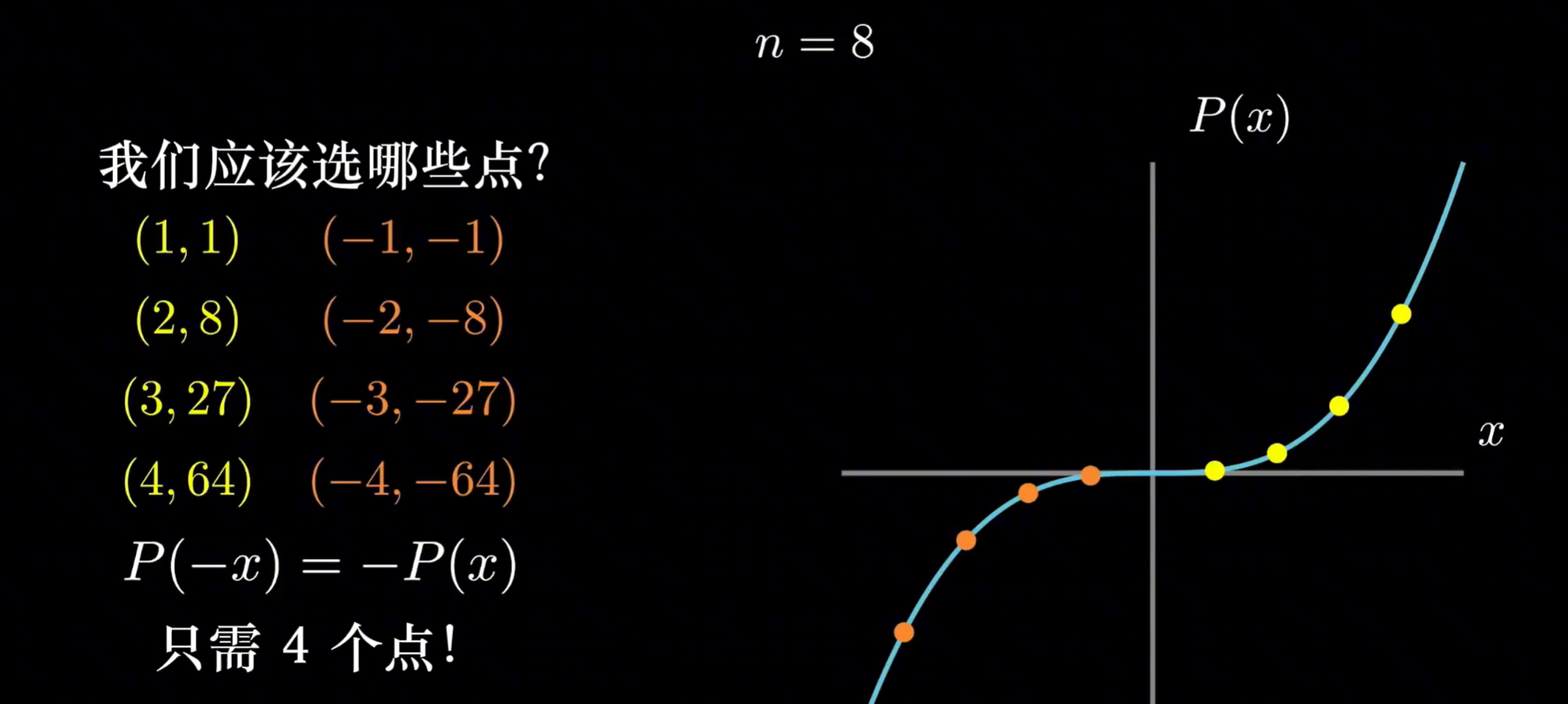
利用上述发现，对于任意一个多项式，它都可以拆成一个奇函数＋偶函数，例如：

由于奇偶函数的性质，其中存在着大量计算重叠，对于 $P(x)$ 来说，每一个正负相对的点都可以简化一次运算。

此外如果我们将P看着x^2的函数，就可以将 $2x^4+7x^2+1$ 写成 $2x^2+7x+1$ ，这样拆分后的多项式的最大次数从5变成了2（也就是从n变成了n/2向下取整），这里我们将一个大问题拆分成了两个小问题，这便是分治的思想了。

现在，计算大多项式的值表示变成了求解两个小多项式的值表示。类似的，我们还可以把小的多项式再进行分解，直到分解成的多项式变成 $P(x)=kx+b$ （k可以等于0）的形式（这样的多项式求值非常方便，最多只需要一步乘法即可，可以作为递归的出口）

但是，如果以一个简单的例子手算一下就会发现其中存在一个问题导致递归中断了，例如上图中，我们将原多项式分解为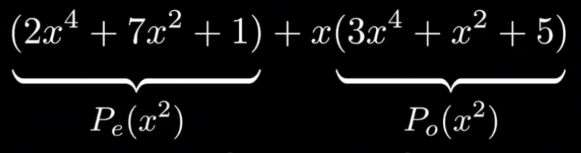

我们为了降低子问题的次数，把x^2看作自变量了，而平方数显然不会为负，这样也就是意味着我们无法找到正负相对的点来简化运算，递归就进行不下去了，这个问题该如何解决呢？

为了能找到正负相对的点，我们需要引入了复平面，下面用一个具体的例子来讲解整个过程

如何将系数表示转为值表示

问题：已知一个由系数表示的多项式，如何快速求解出若干个点（d>=n+1)对应的值。

例如 $P(x)=1+x+x^2+x^3$ ，我们需要至少四个点的对应值，其中这四个点应当是两两正负成对的，记为 $x_1$ 、 $-x_1$ 、 $x_2$ 、 $-x_2$

我们继续上述思路对其分解：

这个多项式可以分解为 $P_e(x)=1+x^2$ 和 $P_o(x)=x(1+x^2)$

那么，对应的两个点也需要正负成对，即 $x_1^2=-x^2_2$ ，再继续：

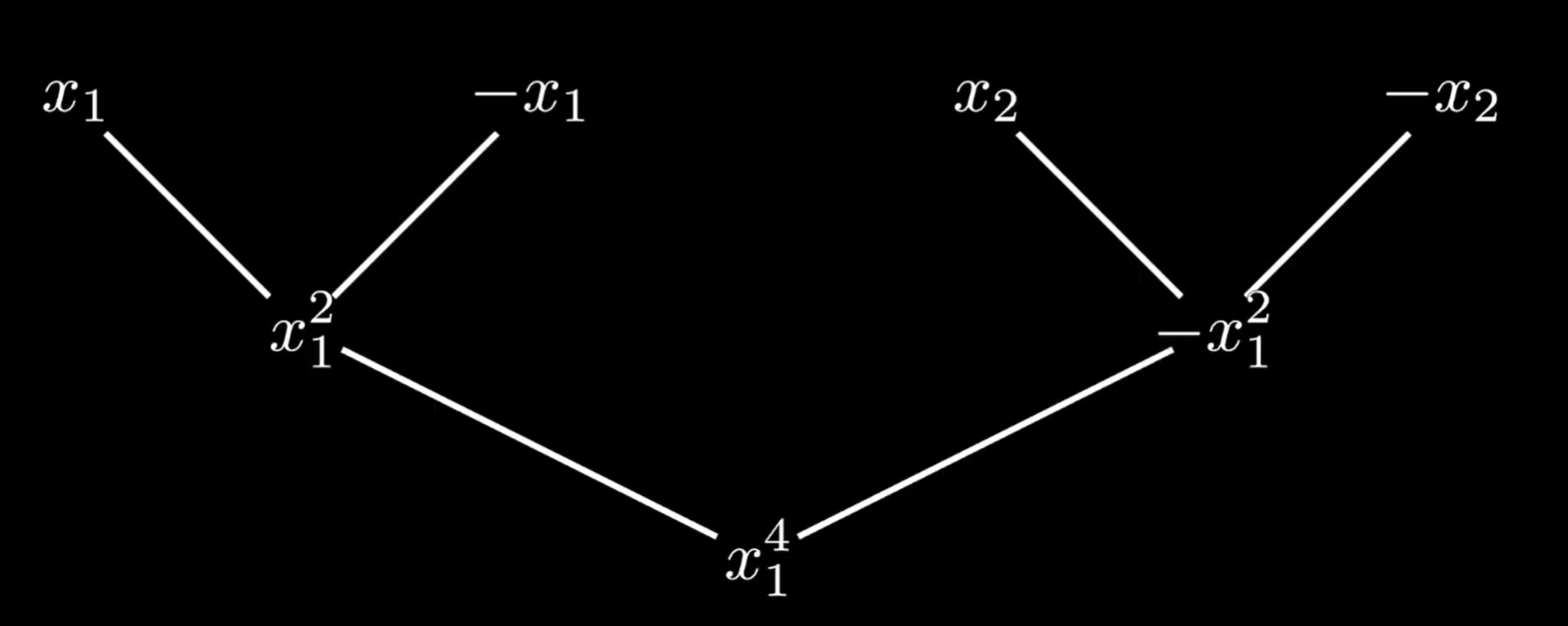
接下来令 $x_1=1$

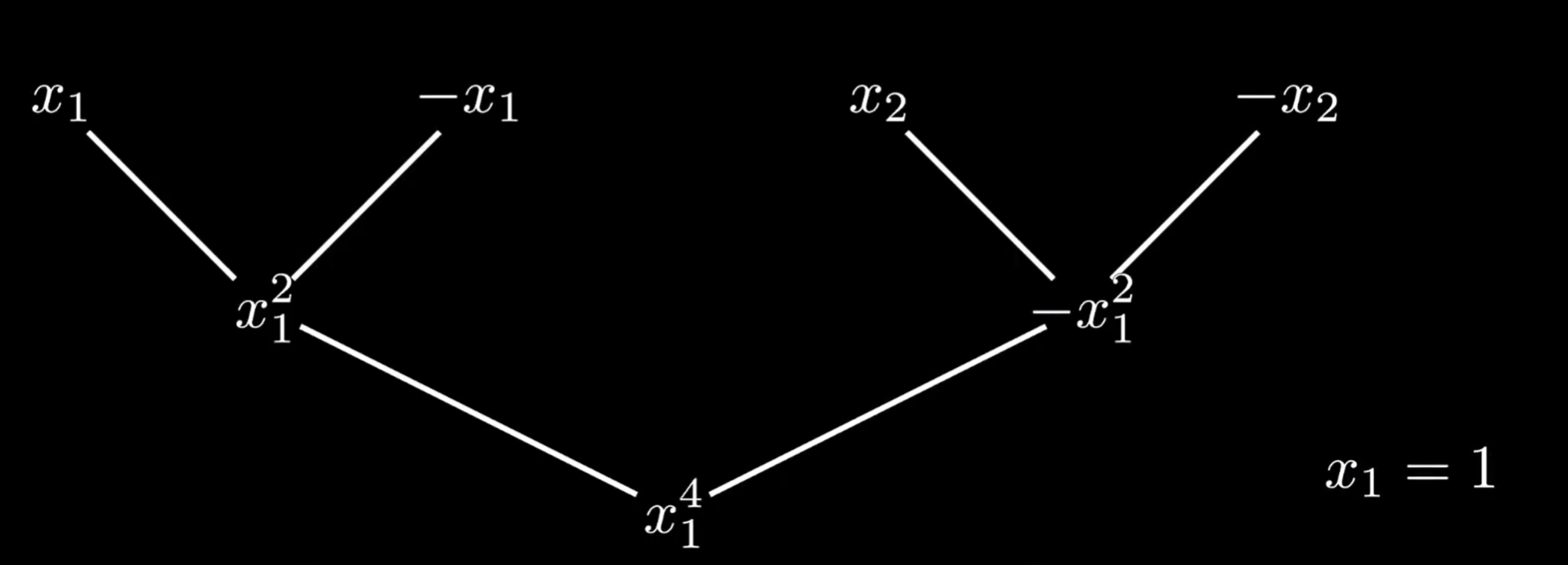
就会解得 $x_1=1$ 、 $-x_1=1$ 、 $x_2=i$ 、 $-x_2=i$ ，这时候我们就会发现，这个过程本质上是在求解 $x^4=1$ ，解得的四个解恰好正负相对。

我们回带到 $P_e(x)=1+x^2$ 和 $P_o(x)=x(1+x^2)$ 中尝试一下：

（1）处理 $P_e(x^2) = 1 + x^2$

代入 $x^2_1=1$ ：得到 $P_e(1) = 1 + 1 = 2$
代入 $x^2_1=-1$ ：得到 $P_e(-1) = 1 + (-1) = 0$

（2）处理 $P_o(x)=x(1+x^2)$

代入 $x^2_2=1$ ： $P_o(1) = 1 \cdot P_e(1) = 2$
代入 $x^2_2=-1$ ： $P_o(-1) = i \cdot P_e(1) = i \cdot 0 = 0$

而 $P(x)=1+x+x^2+x^3$ 等于 $P_e(x)+P_0(x)$ ，这样我们就快速计算出了四个点的值。

这个方法可以推广吗？答案是肯定的：对于n次多项式，只需要求解 $x^n=1$ 即可。（这里其实有一点小问题：例如 $x^7=1$ ，求解出来的七个根肯定无法两两对应，对于这种情况，要么直接求解 $x^8=1$ ，要么对算法本身进行一些小修改，但不影响FFT的本质思想，因此在这里不做区分），为了求解 $x^n=1$ ，我们需要引入n次单位根。

n次单位根

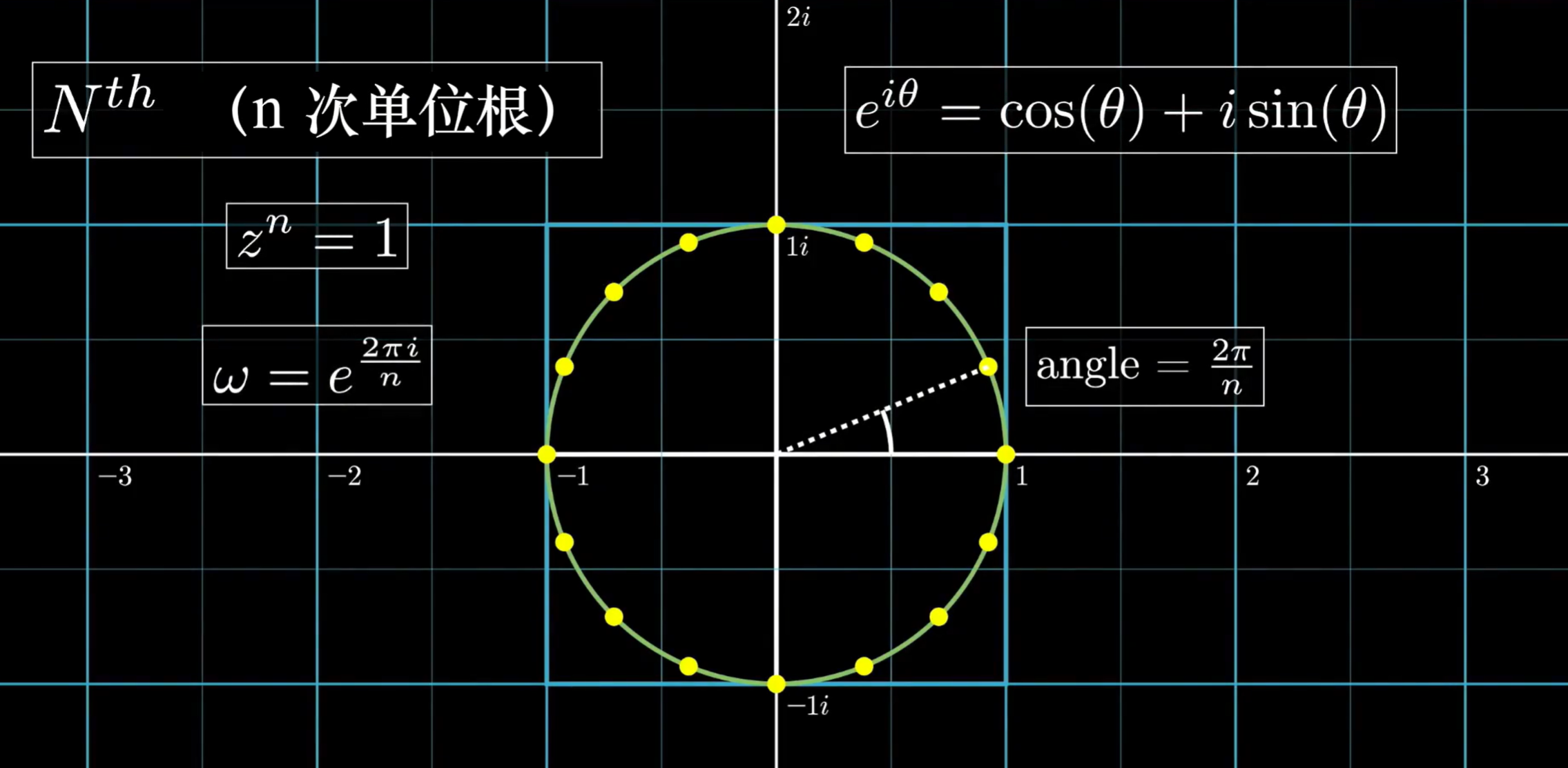
这里以 $x^8=1$ 为例讲解一下，对于一个单位圆，我们可以将其分成n份，每一分对应了 $2\pi /n$

定义单位根的生成元 $\omega = e^{\frac{2\pi i}{n}}$ ，例如当 n=8时，生成元 $\omega = e^{\frac{2\pi i}{8}} = e^{\frac{\pi i}{4}}$ ，结合欧拉公式 $e^{i\theta}=\cos\theta+i\sin\theta$ ，它的具体形式是 $\cos\frac{\pi}{4} + i\sin\frac{\pi}{4} = \frac{\sqrt{2}}{2} + i\frac{\sqrt{2}}{2}$ 。

这八个点是正负相对的（即在单位元中关于原点对称）更重要的是，如果我们对这八个点进行平方

剩下的四个点仍然是正负相对的，再进行平方仍是这样的结果，这就使得递归可以进行下去了。

概述FFT的核心算法

首先FFT以一个n-1次的多项式的系数表示作为输入，目标是计算 $P(x)$ 在 n 次单位根的所有幂次 处的值 —— 这些单位根是 $\omega^0, \omega^1, \dots, \omega^{n-1}$ ，其中 $\omega = e^{\frac{2\pi i}{n}}$ 是 n 次单位根的生成元。当多项式的规模n=1时（只剩 1 个系数），FFT 不需要再拆分，可以作为递归的出口。

接下来是 FFT 提速的关键步骤 ——把原多项式拆成两个规模减半的子多项式：

左边框：偶数项多项式 $P_e(x^2)$ 系数是原多项式的偶数位系数 $[p_0, p_2, \dots, p_{n-2}]$ （比如 $n=8$ 时，取第 0、2、4、6 位系数），要计算它在 $\omega^0, \omega^2, \dots, \omega^{n-2}$ 处的值（这些是 $\frac{n}{2}$ 次单位根）。
右边框：奇数项多项式 $P_o(x^2)$ 系数是原多项式的奇数位系数 $[p_1, p_3, \dots, p_{n-1}]$ （比如 $n=8$ 时，取第 1、3、5、7 位系数），求值点和 $P_e(x^2)$ 完全相同。

这一步递归的输出是

$y_e$ ：是 $P_e(x^2)$ 在子单位根处的取值列表（子 FFT 的结果）。
$y_o$ ：是 $P_o(x^2)$ 在子单位根处的取值列表（另一个子 FFT 的结果）。

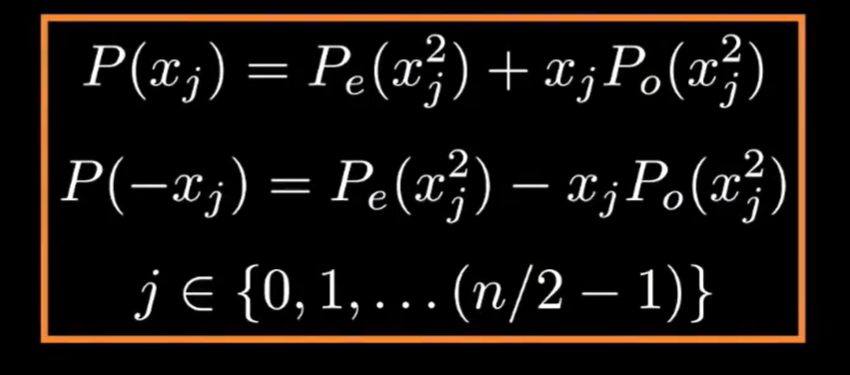
最后，我们将递归的输出结合，即得到了原始多项式在每个单位根下对应的值，不过，结合单位根的表示方式，这个式子还可以写出如下表达：

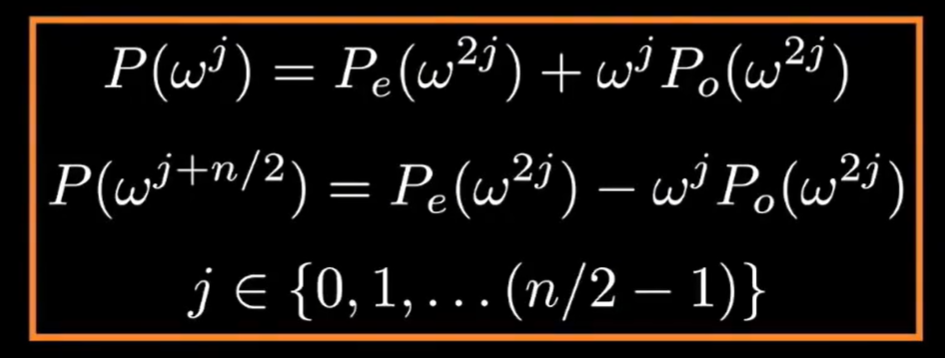
我们将这一步骤整理成代码：

这里看到求值所用的表达形式和我们上面的两种都不同，这是因为其利用了递归输出 $y_e$ 、 $y_o$ 的输出进行转换，即：

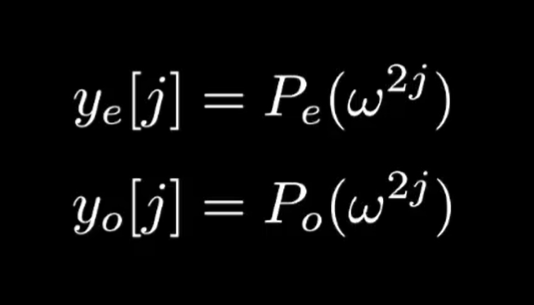
至此，我们完成了FFT算法的核心。即将系数表示转换为值表示。

再回顾一下整个算法的过程

现在我们已经利用FFT将系数表示转换为值表示，而乘法运算是很简单的，直接相乘即可，之后我们会得到 $C(x)$ 的值表示，那么问题来了，如何将值表示转换为系数表示呢？这就是FFT算法的另一个巧妙之处

如何逆置FFT

表面上看，这又是一个很大的工程，但实际上，我们从值表示法中证明d+1个点可以唯一确定一个d次多项式时得到的矩阵表达中可以发现：

这个矩阵将 $x$ 计算得到 $P(x)$ ，如果这个矩阵可逆，那我们不是直接就可以通过求逆的发生从 $P(x)$ 变回 $x$ 了吗？实际上这个矩阵的可逆已经在之前证明过了，不过这里需要对矩阵进行小修改，因为我们实际上带入的并不是 $x_0, x_2, \dots, x_{n-1}$ ，而是 $\omega^0, \omega^1, \dots, \omega^{n-1}$ ，带入之后的矩阵为：