上一节的最后是标准正交基,其需要满足各个向量之间正交且范数为1,接下来讲标准正交基的重要应用——傅里叶展开与施密特正交化。
傅里叶展开

若是内积空间
的标准正交基,则对任意
,可展开为:
其中傅里叶系数:在基
下的坐标;
傅里叶级数
首先我们回忆一下傅里叶级数是怎么来的:



同样的方法也可以求解出,这样就得到了最常见的傅里叶级数的形式。
向量的傅里叶展开
下面我们来看如何对一个向量进行傅里叶展开:
1、函数内积的定义
首先我们需要定义一下两个函数如何做内积,在之前我们定义向量内积时,说过它本质上就是两个向量的每个对应分量做乘积再求和,但向量毕竟是离散的,而函数是连续的,连续的内积该如何定义呢?

高数中有提到:离散下的求和对应在连续下就是积分,所有函数内积定义为两个函数先相乘,在对乘积做积分。对于傅里叶变换定义在上,它的内积如上图所示。
2、标准正交基

大家可以自行检验这个集是否符合,对于范数,可以分为常数、cos、sin三类检验范数是否为1;对于内积,也可以分常数、cos、sin三类之间作内积看是否为0;
3、傅里叶展开

傅里叶展开与傅里叶级数的联系
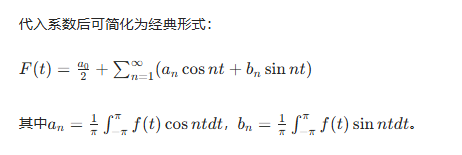
讲傅里叶系数带入之后即可变为傅里叶级数。带入计算后可发现对应系数有下面关系:
,即
;
,即
;
,即
。
至此,就完成了如何把一个函数通过标准正交基的方式进行傅里叶展开。事实上,傅里叶展开的本质就是把任意一个周期函数写成正余弦函数的线性表示。
施密特正交化
所有有限维内积空间都存在标准正交基,施密特正交化的作用是将向量空间中一组任意的集变为一组标准正交的基,它的形式毕竟复杂,但理解起来是并不困难的
先以二维空间(平面)为例:
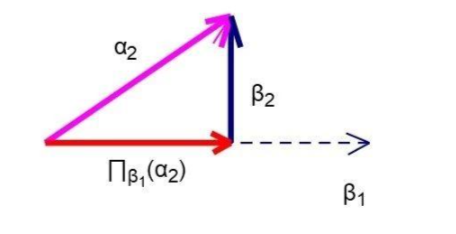
目标:将二维向量空间中的一组基(,其中
与
共线)转换为正交的一组基(
)
首先我们选择为基准,将其单位化后记作
;
如果想要与
正交(即垂直),从向量加减的角度来看,需要
减去
在
上的投影,这样得到的
恰好与
垂直,再进行单位化即可;
现在的目标变为如何求解在
上的投影;(投影的本质:就是需要原向量的长度+投影向量的方向)
从三角函数的角度来看,这个问题非常好解决,即乘上
(
是
的夹角)
借助这个想法,得到在
方向上的投影向量,需要将 “投影长度” 乘以
方向的单位向量(即
),因此投影向量为:
将代入上式,化简得:
最后,再用即得到了
对应二维施密特正交化总结如下:
1、
2、
同样的,三维施密特正交化也是这样,将第三个向量减去在前两个已经正交化的投影即可。
这里推荐一个GIF:三维施密特正交化可视化(我插入文章中的GIF太小了,这里是原文中的第一张动图,原文写的非常好,所有推导过程附带图片):
对应任意的维度,施密特正交化公式如下:
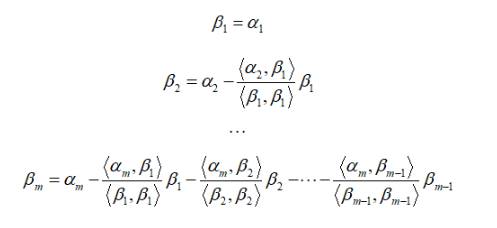
施密特正交化的向量形式与矩阵形式

1、向量形式

这个过程与我们之前推导的一致,只不过写成了求和的形式
2、矩阵形式

对于施密特过程的第步,记已构造的前
个标准正交向量为
,将它们按列拼接成矩阵:

向量在
上的正交投影为:
再用减去投影
,进行单位化即可写成矩阵表示。
(正交投影矩阵后续还会再介绍,这里大家理解它的作用即可)
从施密特正交化到QR分解

设矩阵的列向量线性无关(列满秩),对其列向量应用施密特过程,得到列空间
的标准正交基
。
时:
;
时:
。
为什么是这种形式:


接下来,将这一关系写成矩阵形式:
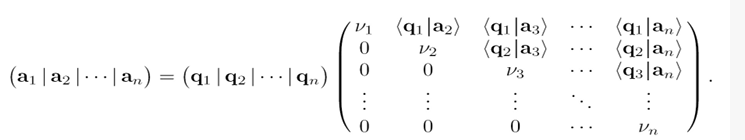
这里,我们实际上把一个矩阵分解为了正交矩阵Q,和上三角矩阵R。
QR分解

对列满秩矩阵(列向量线性无关),可唯一分解为:
其中:
的列是
的列空间
的标准正交基(满足
);
是上三角矩阵,且对角线元素均为正数

例子:

我觉得实际上求解中不需要这样做
可以先用施密特正交化求解出Q矩阵,由于Q是正交矩阵,其逆矩阵就是它的转置,因此,直接用Q的转置乘上A即可得到R矩阵。这种方法和上图本质上是一样的,只不过上图是一个一个算,这种方法是一起求出,对于手算来说更方便一些。



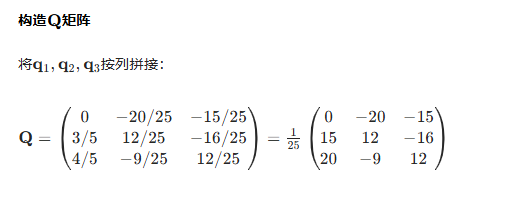





















矩阵分析与应用 国科大&spm=1001.2101.3001.5002&articleId=154955512&d=1&t=3&u=835742495135450f9a92450f3ef767d5)
 1444
1444

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








