C++ 算法学习四（直线、抛物线拟合）

好久没写博客了，忘了怎么开场，哈哈，小编在从事车道线检测，以及机器学习算法线性回归时都用到了线性拟合与多项式拟合，其实可以直接通过opencv的API接口也可实现，具体可见

polynomial_curve_fit(points,1, A);

但是嵌入式平台木有opencv, 于是就详细研究了一下其中数学原理，用C++ 在嵌入式平台直接实现了一下；
先上结果图吧

直线拟合

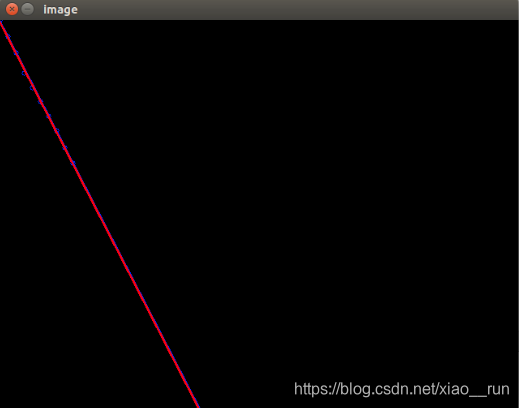
曲线抛物线拟合

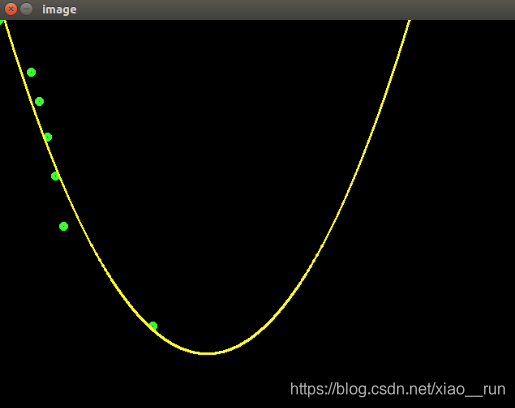
下面我详细记录下拟合过程：
（1）
对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn）。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择：

    （1）用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
    （2）用“残差绝对值和最小”确定直线位