抛物线拟合算法的实现

    最近在写一个程序，其中需要对B样条曲线进行拟合。但是B样条曲线的公式实在复杂，看着就头晕。于是，我将问题进行了简化。一段B样条曲线，可以近似地看成是若干段抛物线构成的，所以，曲线拟合问题就被转换为抛物线拟合问题了。对于抛物线拟合问题，可以使用《计算方法》中的最小二乘法，最后求解线性方程组的地方，用的是高斯消去法。本文用C#实现了这两种算法。

    最小二乘法是一种数据优化技术，在已经得到一组数据的情况下，通过最小化误差平方和的办法，找出最接近的函数。关于最小二乘法的详细说明，可以查看维基百科，本文直接把其中的公式拿来使用。

    假设有一组实测的坐标点数据，绘制在窗体上，效果如下图所示：

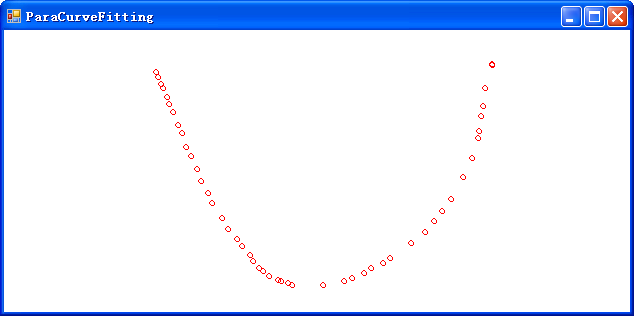
    从图上可以看出，这非常接近一条抛物线。我们将抛物线定义为：a + b*x + c*x^2 = f(x)

    我们可以很方便地计算出：n、Σx、Σx^2、Σx^3、Σx^4、Σy、Σx*y、Σx^2*y。C#代码如下（变量开头的s表示sigma）：

int n = points.Count;
double sx = (double)points.Sum(c => c.X);
double sx2 = (double)points.Sum(c => Math.Pow(c.X, 2));
double sx3 = (double)points.Sum(c => Math.Pow(c.X, 3));
double sx4 = (double)points.Sum(c => Math.Pow(c.X, 4));
double sy = (double)points.Sum(c => c.Y);
double sxy = (double)points.Sum(c => c.X * c.Y);
double sx2y = (double)points.Sum(c => Math.Pow(c.X, 2) * c.Y);

    根据上述数据，我们可以构造一个线性方程组，其正规形式如下：

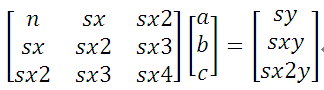
    对于线性方程组，可以使用高斯消去法来求解。我实现了一个通用的高斯消去算法（Gauss），将上述参数代入后，得到一组唯一解：-557.884 + 5.15*x -0.008*x^2 = f(x)
    拟合效果如下图所示（红色是实测数据，蓝色是拟合的抛物线）：

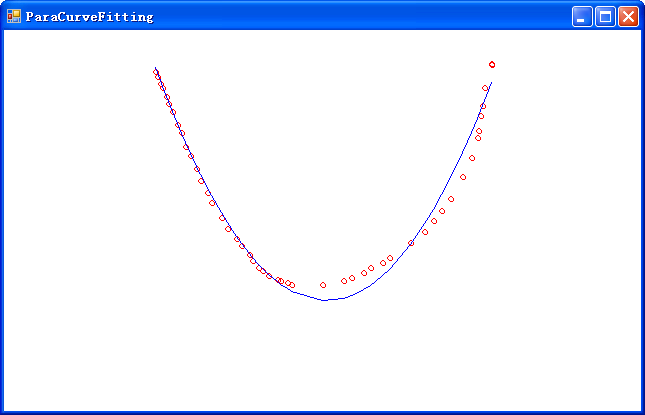
    完整的C#源代码如下（感谢“zhuangzhuang1988”同学的提醒，我对Gauss方法进行了改进，加入了主元选择，以提高计算精度）：

View Code

public partial class Form1 : Form
{
    public Form1()
    {
        InitializeComponent();
    }

    private string testData = "151,41;153,46;156,53;158,57;162,66;164,73;168,81;173,94;177,102;181,116;186,125;192,138;196,150;203,162;207,172;217,187;223,198;232,208;237,215;245,224;248,230;254,237;258,240;264,245;273,249;276,250;283,252;287,254;318,254;339,250;347,247;359,242;366,237;378,232;385,227;406,212;420,201;429,190;437,180;446,168;458,146;467,127;473,107;474,100;476,85;478,75;480,57;487,34;487,33";

    /// <summary>
    /// 解析实测数据。