001 二极管和MOSFET

摩尔定律

• 集成电路上可以容纳的晶体管数目每18个月翻一倍
• 时钟频率区域饱和
• 功耗趋于饱和

MOSFET

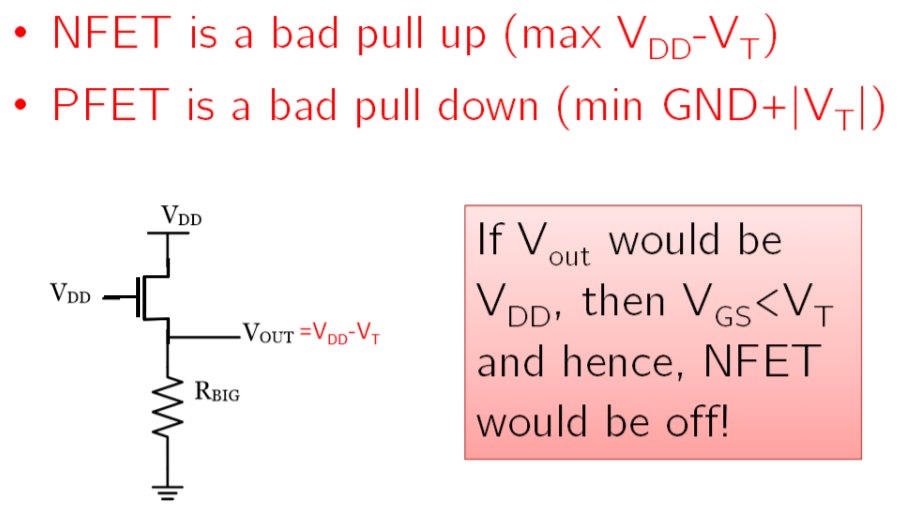
阈值电压

$$V_T=V_{T_0}+\gamma (\sqrt{|2{\varphi }_F+V_{SB}|}-\sqrt{|{\varphi }_F|})$$

• $V_{T_0}：V_{SB}=0时的经验值$
• $\gamma ：体效应系数，\approx 0.4V$
• ${\varphi }_F：费米势，受掺杂影响，{\varphi }_F={\varphi }_{T}log(\frac{N_A}{n_i})$
• $V_B\uparrow ，V_{SB}\downarrow ，V_T\downarrow ，开关速度\uparrow$
• $V_B\downarrow ，V_{SB}\uparrow ，V_T\uparrow ，漏电流\downarrow ，静态功耗\downarrow$

电流电压特性

可变电阻区（线性区）

$$I_{DS}={\mu }_n{C}_{ox}\frac{W}{L}[(V_{GS}-V_T)V_{DS}-\frac{V_{DS}^2}{2}]$$

• $V_{DS}<V_{GS}-V_T$
• $L较大,>0.25\mu m$
• $对于较小的V_{DS},I_{DS}与V_{DS}线性相关$

饱和区

$$I_{DS}=\frac{1}{2}{\mu }_n{C}_{ox}\frac{W}{L}(V_{GS}-V_T{)}^2$$

• $V_{DS}>V_{GS}-V_T$
• $L较大,>0.25\mu m$
• $I_{DS}不再是V_{DS}的函数$

沟道长度调制

$$I_{DS}=\frac{1}{2}{\mu }_n{C}_{ox}\frac{W}{L}(V_{GS}-V_T{)}^2(1+\lambda V_{DS})$$

• $\lambda ：经验参数$
• $反比于沟道长度L$

短沟道效应

• 短沟道器件载流子迁移速度提前达到饱和
• quadratic（二次）区域减小，linear（线性）区域增加

亚阈值

• $V_{GS}<V_T$时，FET关断时，沟道依旧有一定导电性
• 增加静态功耗

纳米晶体管

• 深亚微米器件：$V_T=f(L,W,V_{DS})$
• $L\downarrow ,V_T\downarrow$
• 漏极诱导势垒降低(drain-induced barrier lowering)：$V_D\uparrow ,漏极pn结耗尽区\uparrow ,V_T\downarrow ,V_T=V_{T_0}-{\lambda }_d{V}_{DS}$
• 高电场下，电子会隧穿栅极氧化物，形成栅极漏电流，增加器件静态功耗$(L<=100nm)$
• 相较$Si{O}_2$，高$K$材料的电容大60%，栅极漏电流减小>100%

热载流子效应

• 阈值电压随时间漂移
• 电子或空穴隧穿到栅极氧化物($1V/\mu m$)
• $nmos$的$V_T$增加，$pmos$的$V_T$减小

CMOS latch-up

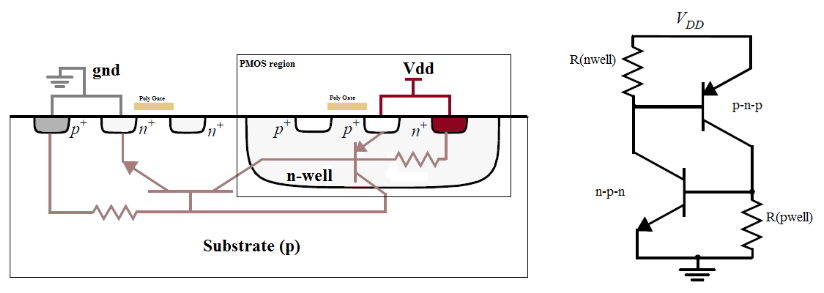
• 一个BJT打开后，电流会打开另一个BJT，正向反馈，即使输入消失，输出也依旧持续
• 降低R(nwell)、R(pwell)，使得V=IR低于阈值电压，不会打开BJT