Dijkstra算法解决单源最短路径

最新推荐文章于 2022-04-13 10:23:22 发布

x__1998

最新推荐文章于 2022-04-13 10:23:22 发布

阅读量406

点赞数

CC 4.0 BY-SA版权

分类专栏：图论

本文链接：https://blog.youkuaiyun.com/x__1998/article/details/79718670

图论专栏收录该内容

5 篇文章

订阅专栏

本文详细介绍Dijkstra算法的应用，包括如何求解从一个起始节点到图中其他所有节点的最短路径。文章通过实例演示了算法的具体步骤，并提供了完整的C++实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Dijkstra用于解决一个节点到其他任意节点的最短路径值。其值用一个dis数组保存。

首先给出一个有向图使用邻接矩阵储存。

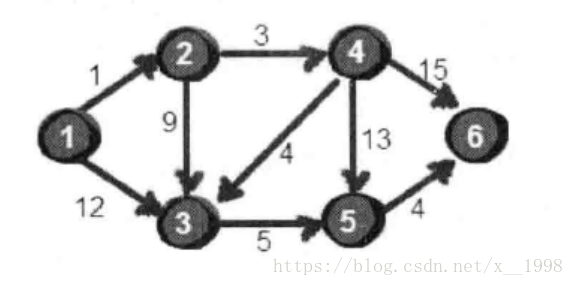
dis数组初始化为1节点到其他节点的距离。

inf

初始化无法直达的节点都表示为无穷大（inf）。

接下来在这个数组中寻找最近的节点-->2。

然后通过2节点为起点去优化dis数组。很明显2号节点到3号节点权值为9，1->2->3小于1->3的权值，于是将dis[3]=10。

inf

3号节点和4号节点在第一轮优化中得到更新。

第二轮优化时，再找出最短路径的点，但是应该注意到已经作过起点的点不能再被选中。于是排除1，2节点最短的是4号。

第三轮优化，排除1，2，4。得到最短的是3。

第四轮优化，排除1，2，3，4得到最短的是5。

注意有两个数组需要初始化

首先需要初始化map邻接矩阵对角线为0其余全为inf。

读完边之后初始化dis数组将其值都设为1号节点到其他节点的初始值。

#include <iostream>
#include <cstdio>
#include <cstring>
#define inf 0x3f3f3f3f
using namespace std;

int m,n,map[101][101],dis[101],book[101];

void Dijkstra(){
	int i,j;
	book[1] = 1;
	for (i = 1;i < m; i++){
		int min = inf,total;
		for (j = 1;j <= m; j++){
			if (min > dis[j] && !book[j]){
				min = dis[j];
				total = j;
			}
		}
		book[total] = 1;
		for (j = 1;j <= m ;j++){
			if (dis[j] > map[total][j] + dis[total]){
				dis[j] = map[total][j] + dis[total];
			}
		}
	}
	for (i = 1;i <= m; i++)
		printf ("%d%c",dis[i],i==m?'\n':' ');
}

int main ()
{
	scanf ("%d%d",&m,&n);
	int i,j;
	for (i = 1;i <= m; i++){//初始化邻接矩阵 
		for (j = 1;j <= m; j++){
			if (i == j)
				map[i][j] = 0;
			else
				map[i][j] = inf;
		}
	}
	for (i = 1;i <= n; i++){
		int a,b,c;
		scanf ("%d%d%d",&a,&b,&c);
		map[a][b] = c;
	}
	for (i = 1;i <= m; i++){
		dis[i] = map[1][i];//初始化dis数组将其值都设为1号节点到其他节点的初始值
	}
	Dijkstra ();
	return 0;
}