本文深入讲解了Dijkstra算法的基本原理及其实现细节，包括如何利用贪心策略寻找单源最短路径，以及如何通过优先队列提高算法效率。此外，还提供了两个实战案例，帮助读者更好地理解算法的应用。
一.算法原理
1.基本原理
Dijkstra算法是利用广度优先搜索思想（BFS）+ 贪心策略的一种单源最短路径算法，从Bellman Ford算法演化而来，但是核心的松弛（Relaxation）思想并没有变：
RELAX(u, v, w)
if v.d > u.d + w(u,v)
v.d = u.d + w(u,v)
v.π = u
不同的Dijkstra算法加入了一个优先队列用来获取每次离起点最近的点。该算法以起点为中心，将相邻边加入到优先队列中，记录每一个点到源点的最近距离，并维护着离源点最近的那个结点。
每趟从此队列中获取到获取其中距起点最近的点，在该点利用松弛操作(relaxation)更新该点的各相邻节点到源点的最近距离(这里用到了贪心算法原理), relaxation操作其实就是如果相邻结点经过该节点比不经过该节点时到源点的距离小，那么就缩短该相邻结点到源结点的距离，存入到优先队列中，如果已经加入到优先队列中，则使用优先队列的DECREASE-KEY操作来更新该结点到源点的距离，这个操作的时间复杂度一般都取决于优先队列的底层实现。
伪代码：
DIJKSTRA(G,w,s)
//记录已访问结点
S = ∅
//初始化待访问的优先队列
Q = G.V
while Q!= ∅
u = EXTRACT-MIN(Q)
S = S ∪ {u};
for each vertex v Q.Adj(u)
RELAX(v)
Dijkstra算法的时间复杂度根据优先队列的实现不同而不同，如果优先队列是用二叉堆来实现，那么EXTRACT-MIN操作与DECREASE-KEY操作的时间复杂度都为O(lgV)，V是图G顶点的集合，图G中的所有边都被访问过，根据聚合分析，那么松弛操作总耗时为O(E*lgV)，从优先队列获取最近点的总耗时为O(V*lgV)，总的耗时为O(V*lgV + E*lgV)，如何源点对于每一个其他结点都存在路径，也就是说|E| > |V|，那么算法的复杂度可以表示为O(E*lgV)
考虑到经常调用DECREASE-KEY操作，所以如果采用斐波那契队列来实现，DECREASE-KEY操作的时间复杂度为O(1)，整个算法的时间复杂度可以塌缩到O(V*lgV+E)
2.如何保存最短路径?
在pathTo集合中，设置此节点的上一节点。如果这点没有被访问过，就加入到优先队列中，就这样重复操作层层向外遍历，最后就可以生成一个最短路径树，对于从该源点到某一点的最短路径问题，只要看该点是否被访问过，被访问过的点说明存在最短路径，回溯pathTo集合，如pathTo(A) = B, B是使A到源点距离最近的相邻点（由贪心算法可知）,pathTo(B) = C , C是使B到源点距离最近的相邻点,反复操作，直到pathTo(X) = 源点。即可得到最短路径
二.算法实战一
package com.example.Dijkstra;
import java.util.*;
public class Dijkstra {
// <1, [2, 3]>表示节点1的父节点是节点2，到源点距离为3
private Map<Integer, int[]> disTo;
/**
* @param edges 一个节点到其他节点的距离
* [[0, 1, 1], [1, 2, 2]] 表示点0到点1的距离为1，点1到点2的距离为2
* @param n 所有节点个数 1<= n <= 1000
* @param k 源节点 1< k <n
*/
public Map<Integer, int[]> Dijkstra(int[][] edges, int n, int k) {
//通过edges数组生成有向图，使用邻接表存储，用map+list模拟。
//<0, <{1,2}, {2,3}>>表示节点0有1，2两个相邻节点,距离分别为2, 3
Map<Integer, List<int[]>> graph = new HashMap<>();
for (int[] edge : edges) {
if (!graph.containsKey(edge[0]))
graph.put(edge[0], new ArrayList<>());
graph.get(edge[0]).add(new int[]{edge[1], edge[2]});
}
//初始化disTo
disTo = new HashMap<>();
for(int i = 0; i<n; i++)
disTo.put(i, new int[]{0, 0});
disTo.put(k, new int[]{-1, Integer.MAX_VALUE});
//Dijkstra
//省略了最小优先队列，用isSeen数组辅助disTo来取代
boolean[] isSeen = new boolean[n];
while(true){
//得到距离最近点
int candiNode = -1;
int candiDistance = Integer.MAX_VALUE;
for(int i=0;i<n;i++){
int[] temp = disTo.get(i);
if(!isSeen[i] && temp[1]<candiDistance){
candiNode = i;
candiDistance = temp[1];
}
}
if(candiNode == -1) break;
isSeen[candiNode] = true;
if(graph.containsKey(candiNode))
for(int[] edge : graph.get(candiNode)){
if(disTo.get(edge[0])[1]> candiDistance + edge[1]){
//对该点相邻点进行伸缩操作
disTo.get(edge[0])[1] = candiDistance + edge[1];
//更新父节点
disTo.get(edge[0])[0] = candiNode;
}
}
}
return disTo;
}
/**
* 输出结果
* @param disTo
* @param end
*/
public void printPath(Map<Integer, int[]> disTo,int pathTo){
int distance = disTo.get(pathTo)[1];
List<Integer> path = new ArrayList<>();
int temp = pathTo;
path.add(temp);
while (temp!=0 && temp!=-1){
temp = disTo.get(temp)[0];
path.add(temp);
}
System.out.print("从初始节点到节点"+end+"的最短距离为"
+distance+"\n"+"最短路径为：\n"+path.get(0));
for(int i=1;i<path.size();i++){
System.out.print("<--"+path.get(i));
}
}
}
这个实现我没有用优先队列，直接用的数组遍历来获取最近点，采取遍历的方式获取每次迭代的最近节点，会让算法的复杂度达到
O
(
∣
N
∣
2
)
O(|N|^2)
O(∣N∣2)
如果利用最小优先队列这个堆式结构，算法的复杂度会缩小至
O
(
∣
E
∣
+
N
l
o
g
N
)
O(|E|+NlogN)
O(∣E∣+NlogN)
1.测试
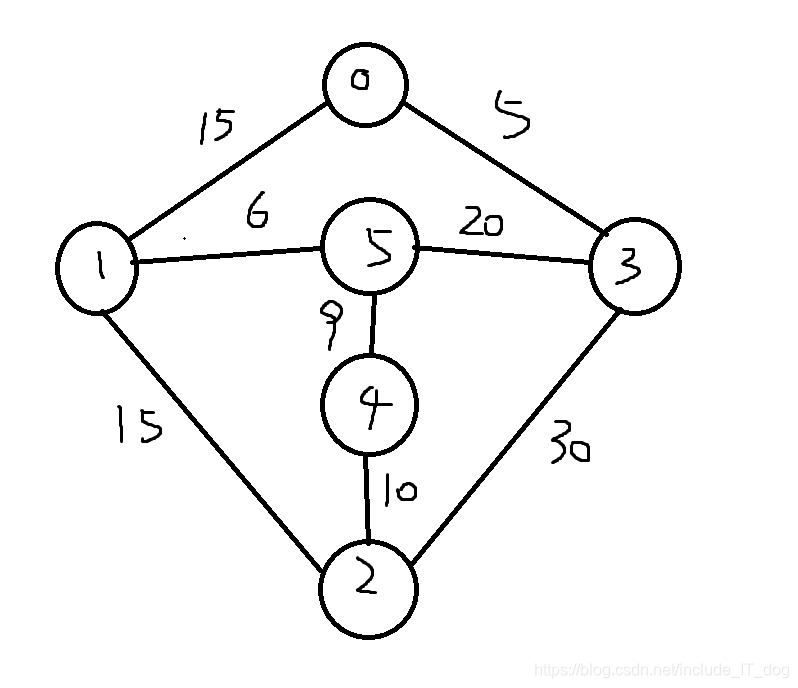
输入：
| edges: | n: | k: | pathTo |
|---|---|---|---|
| {{0, 1, 15},{0, 3, 5}, | 6 | 0 | 4 |
| {1, 5, 6}, {3, 5, 20}, | |||
| {1, 2, 15}, {3, 2, 30}, | |||
| {2, 4, 10}, {5, 4, 9}}; |
预计输出：最短距离：30 路径：0–>1–>5–>4
环境：windows10，java11
2.结果
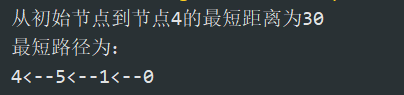
二.算法实战2
教授Leyni喜欢跟罗莉一起玩，这次，XianGe也来了，他们处在一个r * c的矩形区域中。Leyni处在矩形区域的入口外（左上角左侧），XianGe处在矩形区域的出口外（右下角右侧），罗莉处在矩形区域内。现在Leyni要喊话给XianGe，可是声音在这个矩形区域内只能横向或者垂直传递，而且，如果某个罗莉听到了声音（听到声音的罗莉不会阻碍声音继续传播），Leyni可以命令她作为传递者向四周传递一次声音，使得与她同一行同一列的罗莉都能听到声音（如下图右侧情况）；当然，Leyni也可以让听到声音的罗莉不传递（如下图左侧情况）；Leyni处在入口（左上角）的左侧，所以他只能向第一行传递声音；XianGe处在出口（右下角）的右侧，所以他只能接收到最后一行的声音。
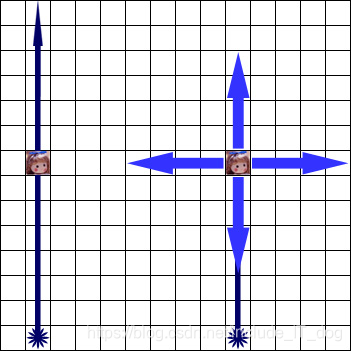
如下图所示是一个3 * 3的矩形区域，在矩形区域内有两个罗莉，Leyni命令她们传递声音，并在入口处传递声音给第一行的罗莉，她同时向四周传递声音，第三行的罗莉收到声音后继续传递，使XianGe听到了声音。
现在给出一个矩形区域的大小和各个罗莉的位置情况，Leyni想知道他最少要命令几个罗莉传递声音才能让XianGe听到，请你帮助他！
Input
本题有多组测试数据，输入的第一行是一个整数T代表着测试数据的数量，接下来是T组测试数据。
对于每组测试数据：
第1行 包含两个以空格分隔的整数r和c (2 ≤ r, c ≤ 1000)，代表着矩形区域的大小。
第2 … r + 1行 这r行包含了一个r行c列的矩阵，由".“和”#“组成，其中”#“表示罗莉，”."表示空。
Output
对于每组测试数据：
第1行 如果Leyni能成功传递声音给XianGe，则输出他最少需要命令多少个罗莉负责传递声音；否则输出-1。
Sample Input
1
3 3
.#.
.#.
.#.
Sample Output
2
这一问题如果用一般的邻接矩阵来表示，很难想到可以使用Dijkstra算法来解决，但是如果转变想法，将无关的坐标忽视掉，只关注萝莉所在的位置，通过萝莉可以将沿着某一行传播的声音转为沿着某一列传播的声音，把行和列都看作点，那么一个萝莉相当于连接两个点的边，如此，最终的实现可以表示为
# include <iostream>
# include <queue>
# include <vector>
using namespace std;
struct edge
{
int from;
int to;
int w;
int pre;
}e[1000000];
int r, c, cnt;
int head[1000000];
bool visited[2001];
int dist[2001];
inline void add(int from, int to, int w)
{
e[cnt].from = from;
e[cnt].to = to;
e[cnt].w = w;
e[cnt].pre = head[from];
head[from] = cnt ++;
}
void SPFA()
{
fill(visited, visited + 2001, false);
fill(dist, dist + r + c, 0x3f3f3f3f);
dist[0] = 0;
queue<int> q;
q.push(0);
while(!q.empty())
{
int n = q.front();q.pop();visited[n] = false;
for(int v = head[n]; v!=-1; v = e[v].pre)
{
int vw = e[v].w, vto = e[v].to;
if (dist[vto] > dist[n] + vw)
{
dist[vto] = dist[n] + vw;
if (!visited[vto])
{
visited[vto] = true;
q.push(vto);
}
}
}
}
if (dist[r-1] == 0x3f3f3f3f)
{
cout << -1 << endl;
}else cout << dist[r-1] << endl;
return;
}
int main(void)
{
int N; cin >> N;
while(N --)
{
cin >> r >> c;
cnt = 0;
fill(head, head + 1000000, -1);
for(int i = 0; i<r; i++)
{
for(int j = 1; j <= c; j++)
{
char tmp; cin >> tmp;
if (tmp == '#')
{
add(i, r + j, 1);
add(r + j, i, 1);
}
}
}
SPFA();
}
return 0;
}
你可能还敢兴趣的图论算法(均附Java实现代码)：
扫一扫
566
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
