Ceres Solver 官方教程学习笔记（八）——数值微分法Numeric derivatives

这篇文章翻译自官方教程Numeric derivatives并且参考了少年的此间的博客文章Ceres-Solver学习笔记(5)

利用analytic derivatives的另一个极端形式是 numeric derivatives，即数值微分法。数值微分法的关键是，目标函数$f(x)$的微分方程可以被写成一个极限形式：

$$Df(x) = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h}$$

前向差分

当然，在计算机上$h$使不可能无限逼近$0$的，那就是选择一个非常小的$h$的值并近似导数

$$Df(x) \approx \frac{f(x + h) - f(x)}{h}$$
上面的公式是最简单的最基本的数值微分。它被称为 “正向差分公式”。

那么，如何在Ceres中实际构建一个数值微分算法过程的呢？主要可以分为两个步骤：
1. 定义Functor给定参数值，Ceres将通过它对给定的$(x，y)$的进行残值计算。
2. 用 NumericDiffCostFunction 来构造一个CostFunction 来封装整个实例。

这里我们仍然延用上一节解析微分算法中的例子。

$$y = \frac{b_1}{(1+e^{b_2-b_3x})^{1/b_4}}$$
$$\begin{split}\begin{align}E(b_1, b_2, b_3, b_4)&= \sum_i f^2(b_1, b_2, b_3, b_4 ; x_i, y_i)\\&= \sum_i \left(\frac{b_1}{(1+e^{b_2-b_3x_i})^{1/b_4}} - y_i\right)^2\\\end{align}\end{split}$$
$$\begin{split}\begin{align}D_1 f(b_1, b_2, b_3, b_4; x,y) &= \frac{1}{(1+e^{b_2-b_3x})^{1/b_4}}\\\end{align}\end{split}$$

具体代码如下：

struct Rat43CostFunctor {
  Rat43CostFunctor(const double x, const double y) : x_(x), y_(y) {}

  bool operator()(const double* parameters, double* residuals) const {
    const double b1 = parameters[0];
    const double b2 = parameters[1];
    const double b3 = parameters[2];
    const double b4 = parameters[3];
    residuals[0] = b1 * pow(1.0 + exp(b2 -  b3 * x_), -1.0 / b4) - y_;
    return true;
  }

  const double x_;
  const double y_;
  //Analytic算法中手动求解Jacobians的部分被拿掉了。
}


CostFunction* cost_function =
  new NumericDiffCostFunction<Rat43CostFunctor, FORWARD, 1, 4>(
    new Rat43CostFunctor(x, y));

这个生成微分的方法对于用户来说工作量最小。用户只需要关注残差计算是否正确和有效。这是第一步。

在进一步深入之前，我们需要先探讨一下前向查分的误差。我们在$x$点附近对$f$进行泰勒展开。

$$\begin{split}\begin{align} f(x+h) &= f(x) + h Df(x) + \frac{h^2}{2!} D^2f(x) + \frac{h^3}{3!}D^3f(x) + \cdots \\ Df(x) &= \frac{f(x + h) - f(x)}{h} - \left [\frac{h}{2!}D^2f(x) + \frac{h^2}{3!}D^3f(x) + \cdots \right]\\\end{align}\end{split}$$
我们用 $O(h)$来表示误差，那么上式写作：
$$\begin{split}\begin{align} Df(x) &= \frac{f(x + h) - f(x)}{h} + O(h) \end{align}\end{split}$$
其中， $$O(h) =- \left [\frac{h}{2!}D^2f(x) + \frac{h^2}{3!}D^3f(x) + \cdots \right]$$

具体实现细节

在上面我们构建了一个Functor。现在我们用NumericDiffCostFunction 实现一种通用的方法（generic algorithm），对我们给定的Functor进行数值微分，这是第二步。虽然 NumericDiffCostFunction的实际实现是非常复杂的，但最终的结果是一个CostFunction，大致代码如下：

class Rat43NumericDiffForward : public SizedCostFunction<1,4> {
   public:
     Rat43NumericDiffForward(const Rat43Functor* functor) : functor_(functor) {} //构造函数
     virtual ~Rat43NumericDiffForward(){}   //析构函数
     virtual bool Evaluate(double const* const* parameters,
                           double* residuals,
                           double** jacobians) const {
       functor_(parameters[0], residuals);
       //Functor中的()操作符重载使之成为了一个函数。在Evaluate函数中parameters是个二级指针，对应二维数组。但是在Functor中parameters是个指向double的指针数组。

       if (!jacobians) return true;
       double* jacobian = jacobians[0];
       if (!jacobian) return true;

       const double f = residuals[0];
       //这里的residuals[0]来自于上面的functor_()。这里的f对应上面表达式的分子的第二项f(x)。

       double parameters_plus_h[4];
       for (int i = 0; i < 4; ++i) {
         std::copy(parameters, parameters + 4, parameters_plus_h);
         //把目前的Parameters[4]中的元素复制到parameters_plus_h[4]中。

         const double kRelativeStepSize = 1e-6;
         //相对步长系数。

         const double h = std::abs(parameters[i]) * kRelativeStepSize;
         //实际步长 = 参数值 * 相对步长系数。

         parameters_plus_h[i] += h;
         //加入h之后的参数

         double f_plus;
         functor_(parameters_plus_h, &f_plus);
         //用functor_（）计算f_plus。f_plus即上面表达式的分子的第一项f(x+h)。

         jacobian[i] = (f_plus - f) / h;
         //计算上面表达式，求得近似的微分值Df(x)。
       }
       return true;
     }

   private:
      scoped_ptr<Rat43Functor> functor_; //作用域指针
 };

std::copy(start, end, std::back_inserter(container));用于容器内容的拷贝。
例如：

int a[3]={1,2,3};
int b[3];
std::copy(a,a+3,b);

注意在上面的代码中选择步骤大小的$h$，不是一个绝对的步长大小，对于所有的参数都是相同的。我们使用相对步长大小$\text{kRelativeStepSize} = 10^{-6}$，这比绝对步长给出了更好的导数估计。这个步长大小的选择只适用于不接近于零的参数值。因此，数字扩散函数的实际实现，使用一个更复杂的步长选择逻辑，在接近于零的地方，它切换到一个固定的步长。上述是一个简化的版本。

中心差分

$O(h)$误差在前向差分公式中是可以的，但不是很好。一个更好的方法是使用中心差分公式：

$$Df(x) \approx \frac{f(x + h) - f(x - h)}{2h}$$
值得注意的事，如果 $f(x)$的值是已知的，那么前向差分公式只需要一次额外的计算，但是中心差分公式需要两次评估函数计算。使用中心差分的代价是它的两倍。那么，额外的计算真的值得吗?
为了回答这个问题，我们再次来计算中心差分公式中的近似误差：
$$\begin{split}\begin{align} f(x + h) &= f(x) + h Df(x) + \frac{h^2}{2!} D^2f(x) + \frac{h^3}{3!} D^3f(x) + \frac{h^4}{4!} D^4f(x) + \cdots\\ f(x - h) &= f(x) - h Df(x) + \frac{h^2}{2!} D^2f(x) - \frac{h^3}{3!} D^3f(c_2) + \frac{h^4}{4!} D^4f(x) + \cdots\\ Df(x) & = \frac{f(x + h) - f(x - h)}{2h} + \frac{h^2}{3!} D^3f(x) + \frac{h^4}{5!} D^5f(x) + \cdots \\ Df(x) & = \frac{f(x + h) - f(x - h)}{2h} + O(h^2) \end{align}\end{split}$$

中心差分公式的误差是$O(h^2)$。这个误差是平方的，而前向差分公式中的误差只会呈线性下降。
在Ceres中，将前向差分转换为中心差分很简单：只需要将NumericDiffCostFunction模板参数中的FORWARD更改为CENTRAL。具体如下：

CostFunction* cost_function =
new NumericDiffCostFunction<Rat43CostFunctor, CENTRAL, 1, 4>(
new Rat43CostFunctor(x, y));

但是，这一点变化在实际中到底意味着什么呢？要搞清楚这个问题，让我们来考虑下面这个函数在$x=1.0$处的导数的问题

$$f(x) = \frac{e^x}{\sin x - x^2}$$ 。
很容易可以求出此处的导数为 $Df(1.0) =140.73773557129658$ 利用这个值作为参考，我们可以计算并绘制出前向和中心差分公式的相对误差。这个相对误差是关于绝对步长值的函数。

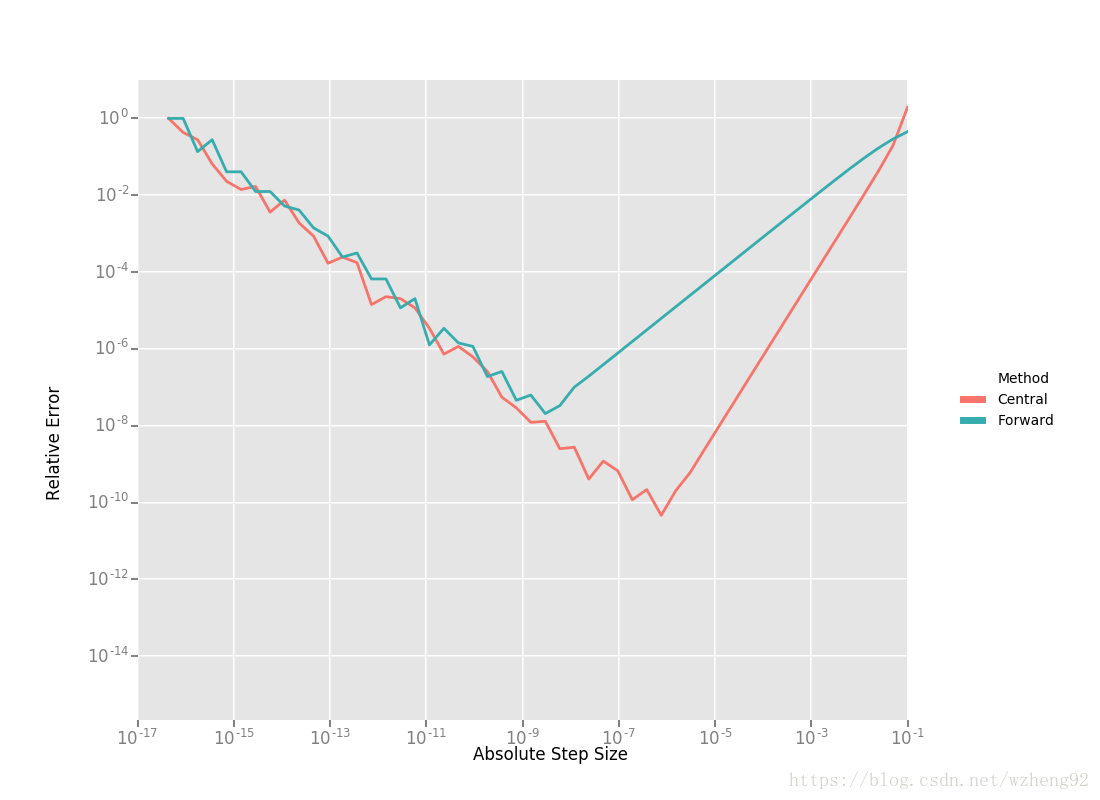
从右到左阅读图表，显而易见的：

1. 这两种差分公式的图形都可以分成两个不同的区域。首先，从一个很大的h值开始，随着截断泰勒级数的影响，这个误差会下降，但是随着$h$的值继续下降，这个误差开始再次增加，因为“舍入”的误差开始占据计算的主导地位。因此，我们不能继续通过降低$h$的的方式，获得对$Df$更精确的估计。我们的近似运算变成了一个明显的限制因素。
2. 前向差分并不是计算导数的一种很好的方法。中心微分公式收敛速度快得多，可以更精确地估计出步长的导数。因此，除非$f(x)$的评估函数运算非常复杂以至于中心差分公式无法负担，否则不要使用前向微分公式。
3. 对于一个糟糕的$h$值，这两个公式都不适用。

这里补充博客文章Ridders求导算法。文章对两种查分方式误差的对比分析写得更清晰。但是这篇文章对于Ridders算法 的介绍不太易懂。

Ridders方法

在上面两种差分方法，精度受到计算机浮点数精度的限制，也就是$h$不能无限小。那么，我们能否得到更好的对$Df$的估计，而不需要如此小的$h$，以至于我们开始碰到浮点数的精度极限？
一种可能的方法是找到一种比$O(h^2)$快得多的方法。这可以通过运用 Richardson Extrapolation来解决微分问题。这也被称为Ridders的方法。

让我们回忆一下，中心差分公式中的误差。

$$\begin{split}\begin{align} Df(x) & = \frac{f(x + h) - f(x - h)}{2h} + \frac{h^2}{3!} D^3f(x) + \frac{h^4}{5!} D^5f(x) + \cdots\\ & = \frac{f(x + h) - f(x - h)}{2h} + K_2 h^2 + K_4 h^4 + \cdots \end{align}\end{split}$$

这里要注意的是$K_2$ $K_4$……独立于$h$，只依赖于$x$。
我们定义：

$$A(1, m) = \frac{f(x + h/2^{m-1}) - f(x - h/2^{m-1})}{2h/2^{m-1}}.$$
观察代入：
$$Df(x) = A(1,1) + K_2 h^2 + K_4 h^4 + \cdots$$
如果我们将步长减半，即令$h = h/2$，则得到另一个中心差分表达式：
$$Df(x) = A(1, 2) + K_2 (h/2)^2 + K_4 (h/2)^4 + \cdots$$
如果我们将第二个表达式乘4然后和第一个表达式联立，可以得到一个新的关于$Df(x)$的表达式，即
$$Df(x) = \frac{4 A(1, 2) - A(1,1)}{4 - 1} + O(h^4)$$
这是$Df(x)$的新近似值，它的截断误差数量级是$O(h^4)$。我们将这一过程进行重复迭代，就可以得到下面的公式：
$$\begin{split}A(n, m) = \begin{cases} \frac{\displaystyle f(x + h/2^{m-1}) - f(x - h/2^{m-1})}{\displaystyle 2h/2^{m-1}} & n = 1 \\ \frac{\displaystyle 4^{n-1} A(n - 1, m + 1) - A(n - 1, m)}{\displaystyle 4^{n-1} - 1} & n > 1 \end{cases}\end{split}$$
其中的参数$n$可以理解为，$A$包含了$Df(x)$原始表达式的前$n$项，这也就意味着误差等级为$O(h^{2n})$。原始公式的前$n$项（如果$n>1$）是包含$f$相关项和$Kh$相关项的，但它们都可以由之前计算出来的$A$推到出来。根据这个公式可以知道$A(n, m)(n>1)$依赖于$A(n-1, m+1)$和$A(n-1, m)$。我们可以把推到过程化成三角形表格如下：
$$\begin{split}\begin{array}{ccccc} A(1,1) & A(1, 2) & A(1, 3) & A(1, 4) & \cdots\\ & A(2, 1) & A(2, 2) & A(2, 3) & \cdots\\ & & A(3, 1) & A(3, 2) & \cdots\\ & & & A(4, 1) & \cdots \\ & & & & \ddots \end{array}\end{split}$$
因此，为了计算$A(n，1)$对增量$n$的值，我们从左向右移动，一次计算一列。每次计算的花费即是两次评估函数$f(x)$的的计算量。计算$A(1,n)$的花费等于对步长大小为$2^{1-n}h$的中心差分的计算。
把这个方法应用到$f(x) = \frac{e^x}{\sin x - x^2}$，从一个相当大的步长$h=0.01$开始，我们得到：
$$\begin{split}\begin{array}{rrrrr} 141.678097131 &140.971663667 &140.796145400 &140.752333523 &140.741384778\\ &140.736185846 &140.737639311 &140.737729564 &140.737735196\\ & &140.737736209 &140.737735581 &140.737735571\\ & & &140.737735571 &140.737735571\\ & & & &\mathbf{140.737735571}\\ \end{array}\end{split}$$
相对于参考值$Df(1.0)=140.73773557129658$，$A(5,1)$的相对误差为$10^{-13}$。比较而言，中央差分公式在相同的步长情况下$0.01/2^4=0.000625$的相对误差是$10^{−5}$。

$A(5,1)$需要$A(4,2)$，$A(4,2)$需要$A(3,3)$，$A(3,3)$需要$A(2,4)$，$A(2,4)$需要$A(1,5)$，所以$A(5,1)$最终对应的中心差分步长是$\frac{h}{2^{5-1}}$

上述内容是针对“数值微分法”的Ridders方法基础。具体的实现是一种自适应模式，它跟踪自己的评估误差，并在达到所需的精度时自动停止。很明晰那，它比前向差分和中心差分公式需要更多计算，但也更加鲁棒和精确。在Ceres使用Ridders法很方便，只需要修改一下NumericDiffCostFunction的模板参数而已。

CostFunction* cost_function =
  new NumericDiffCostFunction<Rat43CostFunctor, RIDDERS, 1, 4>(
    new Rat43CostFunctor(x, y));

下面的图表显示了使用这三种差分方法时，绝对步长大小与相对误差的关系。对于Ridders的方法，我们假设评估$A(n，1)$的对应步长为$2^{1-n}h$。

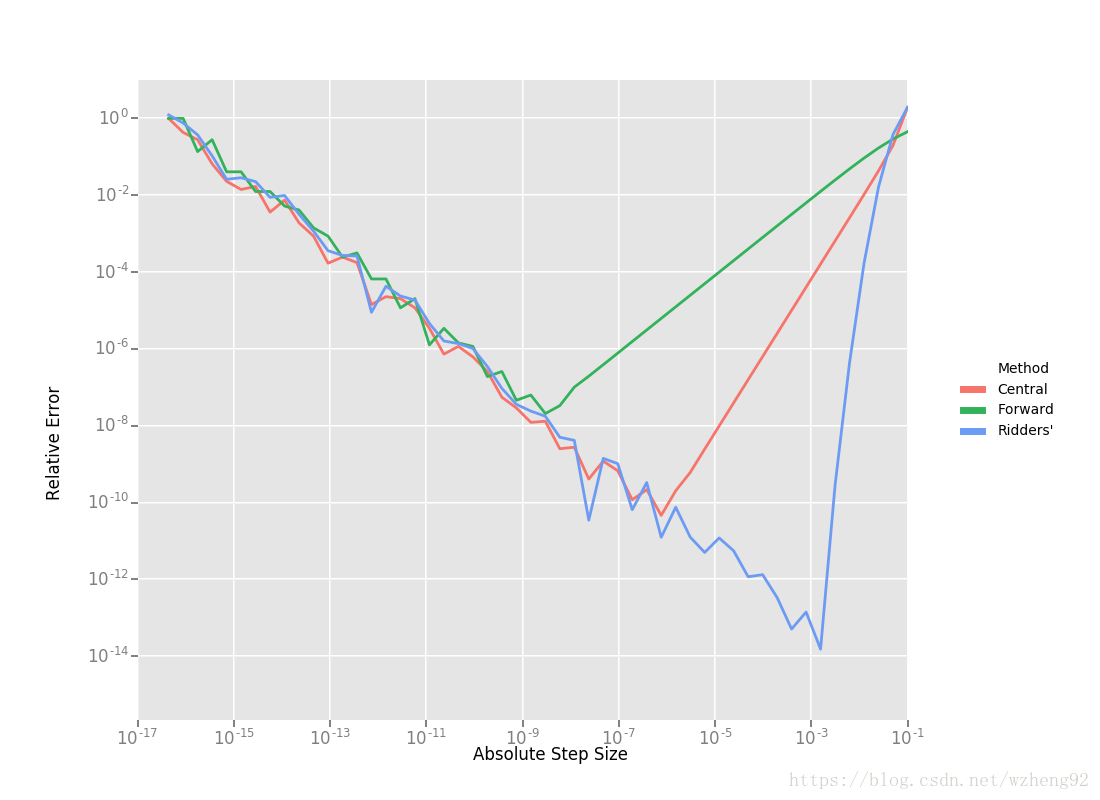
使用Ridders方法计算$A(5,1)$需要计算十次评估函数，对于$Df(1.0)$我们的估算结果比中心差分估算好1000倍（不明白怎么比较的）。为了准确地计算这些数字，计算机的双精度浮点类型≈2.22×10−16。

回到Rat43（上面的曲线拟合问题），让我们对比使用数值微分算法的各种方法的运行效率。

CostFunction	Time (ns)
Rat43Analytic	255
Rat43AnalyticOptimized	92
Rat43NumericDiffForward	262
Rat43NumericDiffCentral	517
Rat43NumericDiffRidders	3760

正如预期的那样，中心差分的运行时间大约是前向差分的两倍，而Ridders方法的运行时间是前两者的好多倍，虽然它的精度也随之显著提高。

建议

当你不能通过分析微分法或自动微分法来计算微分时，就应该使用数值微分算法。通常情况下，这种情况出现在调用一个外部库或函数时。用户不知道它的解析形式，或者即使知道，也无法用 Automatic Derivatives的方式重写它。

当使用数字微分时，尽量使用中心差分法。如果求算时间无关紧要，或者无法为目标函数确定一个适宜的静态相对步长，那么建议Ridders方法。