GTSAM 官方教程学习

0. 前言

年初完成了深蓝学院多传感器融合的课程，接触到因子图，作业中完成了基于ceres库的因子图构建，但存在cost不下降的问题。计划利用gtsam进行重写，开始学习记录。本文主要内容为gtsam官方教程的翻译，结合泡泡机器人公开课56，会在中间穿插自己的理解和应用。但为了记录自己的学习过程，有些理论性已经掌握的内容会稍微省略。
官方git：官方git（https://github.com/borglab/gtsam）
官方教程：官方教程（https://gtsam.org/tutorials/intro.html）

1. 因子图

1.1 序

因子图作为一种概率图模型，是将一个具有多变量的全局函数因子分解，得到几个局部函数的乘积，以此为基础得到的一个双向图叫做因子图。
在面试的过程中，有被问到因子图和位姿图的区别，当时有些懵，这里一起记录。

• 从BA开始说起，BA是SLAM和SFM定义出来的一个优化问题，以重投影误差为误差函数，以每个时刻位姿和所有路标点为优化变量，即将位姿和特征点一起优化。
  

• 位姿图优化在优化几次以后把特征点固定住不再优化，只当做位姿估计的约束，之后主要优化位姿。其节点是位姿，边为两个节点之间的相对运动。

• 因子图是一种概率图，是增量的处理后端优化。每加入一个点，对不需要重新计算的就直接用之前的中间结果，对需要重新计算的再去计算。其节点分为两种，位姿节点与因子节点。 总的来看，BA的计算量最大，需要将位姿与特征点同时优化。位姿图在其基础上减少了对特征点的优化。而因子图和二者区别在于“增量更新”这一点，在储存过去所有信息（会经过边缘化）的基础上并不需要对所有帧进行优化。
  

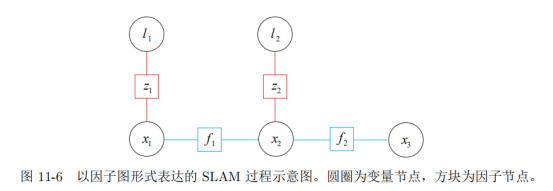
1.2 因子图

1.2.1 贝叶斯网络

将含有三个时间戳的隐马尔科夫模型的贝叶斯网络表示为例。

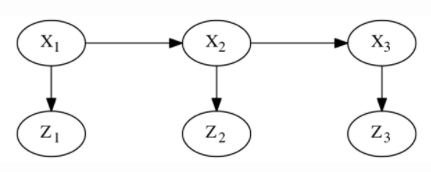
在该贝叶斯网络中，每个节点都和一个条件密度相关联。

• 顶层马尔科夫链展示了先验 $P(X_1)$、转移概率$P(X_2|X_1)$、$P(X_3|X_2)$。
• 在这一过程中，每一帧的的观测量 $Z_t$ 仅与当前时刻的状态量$X_t$有关，服从条件密度 $P(Z_t|X_t)$。
• 给定一组测量值$z_1,z_2,z_3$，可以通过最大化后验概率来求得状态$X_1,X_2,X_3$。即$P(X_1,X_2,X_3|Z_1=z_1,Z_2=z_2,Z_3=z_3)$

这里，观测量$Z_t$是已知的，因此后验概率可以拆分为六个因子的乘积（和一个系数），即三个先验与三个似然因子¹。这里定义$L(X_t;z)\propto P(Z_t=z|X_t)$。

$$P\left(X_1,X_2,X_3\mid Z_1,Z_2,Z_3\right)\propto P\left(X_1\right)P$$