【sklearn第十九讲】高斯混合模型

最新推荐文章于 2025-05-13 07:30:00 发布
原创 最新推荐文章于 2025-05-13 07:30:00 发布 · 6k 阅读 · 10 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#python

本文介绍了sklearn库中的GaussianMixture类，用于学习高斯混合模型。GMM是一种概率模型，数据假设来自多个高斯分布的混合。GaussianMixture类利用EM算法进行拟合，并提供了不同类型的协方差结构。文章讨论了GMM类的优势，如速度快、中立性，以及缺点，如奇性和成分数选择的挑战。BIC准则可用于确定有效成分数，EM算法解决无标签数据的学习问题。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

机器学习训练营——机器学习爱好者的自由交流空间（入群联系qq：2279055353）

一个高斯混合模型(Gaussian Mixture Models, GMM)是一个概率模型，它假设数据来自由若干个未知的高斯（正态）分布组成的混合分布。
sklearn.mixture包能够学习高斯混合模型(Gaussian Mixture Models, GMM), 从GMM抽样，确定适合的成分数。Scikit-learn执行不同的类估计GMM, 对应不同的估计策略。

高斯混合

GaussianMixture对象执行EM(expectation-maximization)算法拟合GMM. GaussianMixture.fit方法从数据学习一个GMM. 给定检验数据，使用GaussianMixture.predict方法给每个样本分派它最可能属于的高斯分布。

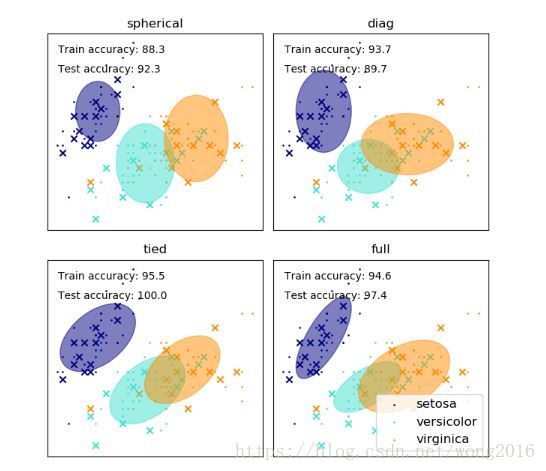
GaussianMixture提供不同的选项约束不同估计类的协方差结构：spherical, diagonal, tied or full covariance.

这里写图片描述

GaussianMixture类的利弊

GaussianMixture类的利：

  • 速度：它是学习混合模型最快的算法。

  • 中立：因为它仅仅最大化似然函数，所以不会使均值偏向0，也不会使成分数偏向形成特定的结构。

GaussianMixture类的弊：

  • 奇性：当对每个混合没有足够多的数据点时，很难估计它的协方差结构。

  • 成分数

最低0.47元/天 解锁文章

200万优质内容无限畅学
Goodsta
关注
混合高斯模型_使用python+sklearn实现高斯混合模型选择
weixin_39638647的博客
12-14 1223
本示例说明了可以使用信息理论标准(information-theoretic criteria)(BIC)的高斯混合模型来进行模型选择。模型选择既涉及协方差类型，也涉及模型中分量(components)的数量。AIC同时也可以提供正确的结果(在本示例中没有显示，以便节省时间)，但如果问题的解决在于确定正确的模型，则BIC会更适合一些。与贝叶斯过程不同，它推断(inferences)过程是...
SKlearn中guassian mixture学习及源码学习(架构)
weixin_38160138的博客
11-13 3117
通过学习sklearn说明中的guasian mixture 的代码学习，深入学习源码，  了解python模块的编写的。 代码： import numpy as np import matplotlib.pyplot as plt from matplotlib.colors import LogNorm 981scikit-learn user guide, Release 0.18
【Scikit-Learn 中文文档】高斯混合模型 - 无监督学习 - 用户指南 | ApacheCN
妳那伊抹微笑的专栏
11-23 1642
sklearn.mixture 是一个应用高斯混合模型进行非监督学习的包，支持 diagonal，spherical，tied，full四种协方差矩阵 （注：diagonal指每个分量分布有各自不同对角协方差矩阵，spherical指每个分量分布有各自不同的简单协方差矩阵， tied指所有分量分布有相同的标准协方差矩阵，full指每个分量分布有各自不同的标准协方差矩阵） ，它对数据进行抽样，并且根据数据估计模型。同时包也提供了相关支持，来帮助用户决定合适的分量分布个数。 ../_images/sphx_g
【深度学习|学习笔记】高斯混合模型（Gaussian Mixture Model，GMM）详解，附代码。
最新发布
2401_89898861的博客
05-13 967
【深度学习|学习笔记】高斯混合模型（Gaussian Mixture Model，GMM）详解，附代码。
混合高斯模型
彬彬侠的博客
12-31 2208
混合高斯模型（Gaussian Mixture Model，简称 GMM）是一种概率模型，通过将数据视为由多个高斯分布（正态分布）的加权组合而生成，适用于聚类、密度估计、数据分布建模等场景。scikit-learn提供了GaussianMixture类，可轻松完成训练、预测和评估。在实际应用时，需要选择合适的成分数（K），常用AIC/BIC进行决策。
【sklearn篇】mixture.GaussianMixture各参数详解以及代码实现
热门推荐
weixin_41861700的博客
04-29 2万+
GaussianMixture 参量 n_components 混合高斯模型个数，默认为 1 covariance_type 协方差类型，{‘full’,‘tied’, ‘diag’, ‘spherical’} full 指每个分量有各自不同的标准协方差矩阵，完全协方差矩阵（元素都不为零） tied 指所有分量有相同的标准协方差矩阵（HMM 会用到） diag 指每个分量有各自不同对角协方...
高斯混合模型
cug_coffee的博客
03-16 373
高斯混合模型，首先说的那就是高斯分布， f(x)=12πσexp⁡(−(x−μ)22σ2)=N(x,σ,μ2) f(x)=\frac{1}{\sqrt{{2\pi}}\sigma}\exp(-\frac{(x-\mu)^2}{2\sigma^2})=N(x,\sigma,\mu^2) f(x)=2π​σ1​exp(−2σ2(x−μ)2​)=N(x,σ,μ2) 对应的均值方差是μ\muμ，σ2\si...
sklearn之高斯混合模型
影子
04-26 6553
什么是高斯分布？ 高斯分布也叫正态分布，也就是常态分布，什么意思呢？比如说男性的身高，假如说有10000个男性的身高，如果再坐标系上标记出来就是一个正态分布，如果形状还不是和上面的图形一样，那说明数据量还不够，如果数据量足够多的情况下， 就会生成上面的正态分布图。事实上任何一种单一的概率分布都符合正态分布，正态分布的形状由平均值μ \muμ和方差σ 2 \sigma^2σ2所决定。 一维正态分布公式：正态分布有两个参数，即期望（均数）μ和标准差σ，σ2为方差。 标准正态分布： ...
使用sklearn实现混合高斯聚类
weixin_44414593的博客
10-16 2256
from sklearn.mixture import GaussianMixture 参数 n_components高斯模型的数量，也是聚类的数量，相当于k-means中的k。 covariance_type方差类型，具体的差异性没有研究过。 tol停止迭代的阈值 reg_covar防止为零的增加数，使用默认即可。 max_iter最大的迭代次数 n_init随机次数，因为GMM算法手随机数影响较大，所以需要多随机几次。算法会保存最优的随机作为最优解。 random_state随机数 属性 **weig
【机器学习】使用scikitLearn对数据进行聚类：高斯聚类GaussianMixture
种一棵树最好的时间是十年前，其次是现在
10-04 3151
生成每个实例时，根据一组权重参数，先选取该实例所属集群的标签，根据标签从k个高斯分布中选取该集群对应的分布，然后再利用高斯分布采样出该实例，就完成了一个新实例点的生成。其中AIC不受实例的数目影响，BIC较AIC对精度的考虑低，对参数量的考虑多，能找出更精简的模型（实例m相当于对参数数量进行了加权）。BIC及AIC的值越小，代表模型越好，可见实例及参数越多，似然函数值越低，代表拟合精度越差，同时算法所用实例及参数越多。p为模型可学习参数量，m为实例数目，L为模型的似然函数最大值。
sklearn应用—高斯混合
sanmi8276的博客
02-16 2204
原文作者：消费金融风控联盟 原文地址：高斯混合模型 一、高斯混合模型 sklearn.mixture是一个应用高斯混合模型进行非监督学习的包，支持 diagonal，spherical，tied，full 四种协方差矩阵，它对数据进行抽样，并且根据数据估计模型。同时包也提供了相关支持，来帮助用户决定合适的分量数（分量个数）。 （译注：在高斯混合模型中，我们将每一个高斯分布称为一个分量，即 component ） 注： diagonal 指每个分量有各自不同对角协方差矩阵 spher...
聚类算法-高斯混合模型GMM
11-03
网上很多的代码都是错误的，特别是广为流传的那份，我已经进行了修改，并在此前提下，对群中心距离是否太近进行了判断，如果群中心太近，那就就将两个中心所代表的两个聚类合成为一个聚类，更符合实际
一文读懂高斯混合模型
m0_74259787的博客
12-29 3355
在扩散模型（Diffusion Models）中，高斯分布扮演着至关重要的角色。这些模型使用一系列逐步添加噪声的过程来将数据逐渐“扩散”到随机噪声，然后再通过逆过程从噪声中恢复原始数据。
机器学习，多输入多输出的线性回归模型代码
weixin_35749545的博客
01-12 629
多输入多输出的线性回归模型可以使用 Python 的 scikit-learn 库来实现。下面是一个简单的代码示例： from sklearn.linear_model import LinearRegression import numpy as np # 训练数据 X_train = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) y_train = ...
【机器学习】sklearn.mixture.GaussianMixture
weixin_38770711的博客
10-15 9025
GaussianMixture(n_components=1, covariance_type=’full’, tol=0.001, reg_covar=1e-06, max_iter=100, n_init=1, init_params=’kmeans’, weights_init=None, means_init=None,  precisions_init=None, random_stat...
GMM 高斯混合模型 聚类 Python实现
csdn_inside的博客
12-26 1万+
原理也不多说了。。大致思路就是把数据建立成k个高斯分布，EM迭代N次。最后看每个点在哪个高斯分布的概率最高，就分到那个分布。 这里的computeGamma函数，用来算第i个簇的后验概率γji，用了2层循环，效率不高，本来想向量化的，搞了半天没搞出来。。干脆就先循环吧。。包括后面的fit方法也是一样。。用了很多循环。 X的shape是(n_samples,n_features) mu的sha...
多输入多输出回归模型（Multiple Input - Multiple Output）
fs01234的博客
01-27 2万+
大家所熟悉的机器学习算法的回归结果通常就是一个变量，而最近项目中遇到一个问题，希望利用多输入变量预测多输出变量，也就是multiple input -multiple output。拿到这个问题，我的思路有两个，一个是利用神经网络算法，毕竟其自身的构造特点就是多输入多输出；另一个是对每一个输出变量构造回归模型，有几个输出就有几个回归模型，当然最好都用同一种算法。在自己思考过后，在网上查阅了资料发现，原来处理多输入多输出回归问题，还有其它高效的处理办法。 具体操作见文献1，具体操作都以python中的skle
SKlearn.mixture
kakak_的博客
04-10 923
GMM Gaussian Mixture Model是EM算法在混合高斯分布的实现 SKlearn.mixture.GaussianMixture n_components: 混合高斯模型个数，默认为1 covariance_type: 协方差类型，默认‘full’ ；‘full’完全协方差矩阵（元素都不为零）‘tied’相同的完全协方差矩阵（HMM会用到） ‘diag’对角协方差矩阵（...
sklearn输出模型参数_机器学习100天-Day1702CART算法和几个超参数
weixin_39522408的博客
11-27 244
说明：本文依据《Sklearn 与 TensorFlow 机器学习实用指南》完成，所有版权和解释权均归作者和翻译成员所有，我只是搬运和做注解。第五章是对支持向量机SVM的系统介绍，阐述支持向量机的核心概念，怎么使用这个强大的模型，以及它是如何工作的。 这应该是第三次做这方面的内容了，贴出另一个比较全面的SVM进阶博客。https://blog.youkuaiyun.com/v_JULY_v/article/d...
sklearn 高斯混合模型
08-16
高斯混合模型（Gaussian Mixture Model, GMM）是一种用于聚类和密度估计的概率模型。在sklearn库中，可以使用sklearn.mixture模块中的GaussianMixture类来实现高斯混合模型。 下面是一个使用sklearn实现高斯混合模型的示例代码： ```python from sklearn.mixture import GaussianMixture # 创建一个高斯混合模型对象 gmm = GaussianMixture(n_components=3) # 假设有一些数据X，将模型拟合到数据上 gmm.fit(X) # 使用训练好的模型进行预测 labels = gmm.predict(X) # 获取每个样本属于各个混合分量的后验概率 probs = gmm.predict_proba(X) ``` 在上面的代码中，我们首先创建了一个GaussianMixture对象，并指定了混合分量的数量（n_components）。然后，通过调用fit方法，将模型拟合到数据集X上。 接下来，我们可以使用predict方法对新的样本进行预测，返回每个样本所属的混合分量的标签。还可以使用predict_proba方法获取每个样本属于各个混合分量的后验概率。 需要注意的是，高斯混合模型是一种非监督学习方法，因此不需要事先标记好的训练数据。它可以用于聚类任务，也可以用于估计数据的概率密度分布。 希望以上信息能对你有帮助！如果还有其他问题，请继续提问。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值