The Theory of Stencil Shadow Volumes

https://www.gamedev.net/articles/programming/graphics/the-theory-of-stencil-shadow-volumes-r1873/

the theory of stencil shadow volumes

这个是对ogl中教程40的模板体积阴影的进一步学习。

shadows used to be just a patch of darkened texture, usually round in shape, which is projected onto the floor below characters or objects in a game. one must be ill informed or naive to think that we can still get away with this kind of sloppy 草率的 ‘hacks’ in future 3D games. there used to be a time 有过一段时间 where shadows are just too expensive to be rendered properly in real-time, but with the ever-increasing power of graphics hardware, failure to provide proper shadows no longer meant mediocre 平庸的 ？？ implementations, it borders on being guilty of criminally under-utilizing the graphics hardware available.

there are many differing shadowing techniques and approaches to implementing shadows and nailing down a best solution is difficult. in order to understand all the approaches and appreciate their differences, 意识到他们的不同。 strengths and weakness, i strongly suggest reading anything and everything about doing shadows in 3D.
你看，作者也建议学习所有的关于阴影的知识，然比较之。

we should not constrain ourselves to just studying shadow volume technique; any shadowing technique is worth a look.

chapter 5 of [13] has a wonderful high-level discussion on most of the known shadowing techniques. to limit the scope of this paper, we shall only discuss the theory and implementation issues of stencil shadow volumes with particular reference to using microsoft’s direct3D api. it would also be good to understand that stencil shadow volume just is not the “end all” shadowing technique.

a discussion on the strengths of differing shadowing technique can be found at [4] with reference to a game setting.
just recently, eric lengyel[11] also presented a very complete article on implementing shadow volumes in opengl at the gamasutra website[17].

the mathematical derivations of lengyel’s article can be found in [12].

going back a few years, there was the famous “Carmack On Shadow Volumes” text file[6], which is nothing more that an email from john carmack of id software to mark kilgard of nvidia about the derivation of the depth-fail shadow volume implementation. it is interesting to note that Carmack independently discovered the depth-fail method while bill bilodeau and mike songy[7] had also presented similar approach to shadow volumes.

consequently, the depth-fail method is now commonly known as “Carmack’s Reverse”.

stencil shadow volume concept

frank crow[8] first presented the idea of using shadow volumes for shadow casting in 1977. Tim heidmann[5] of silicon graphcis implemented Crow’s shadow volume by cunningly 狡猾地 utilzing the stencil buffer for shadow volume counting in IRIX GL.

let us take a look at how the original stencil shadow volume technique works.

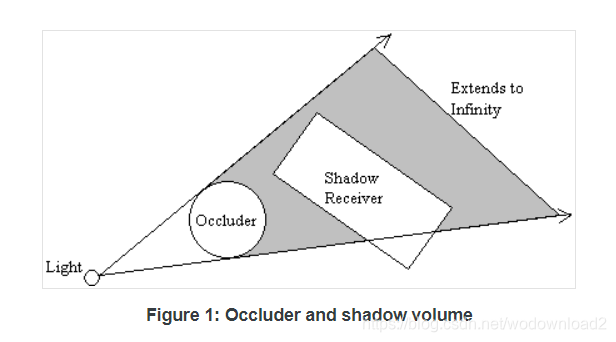
as common convention goes, any objects in a scene that cast shadows are called occluders. as show in figure 1 above, we have a simplistic 2D view (top donw) of a scene with a sphere as the occluder. the rectangle of the right of the sphere is the shadow receiver. for simplicity, we do not take into account the shadow volume created by the rectangle. the shaded region represents the shadow volume, in 2D, created by the occluder. the shadow volume is the result of extruding 挤出 ，想起来3dmax的挤出命令没？？ the silhouette edges from the point-of-view of the light source to a finite or infinite distance.

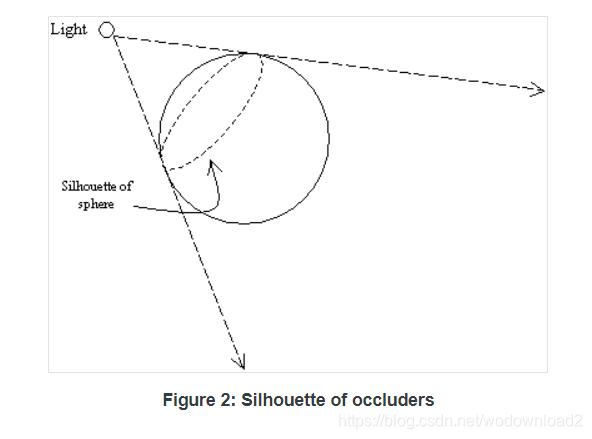
figure 2 shows the probable silhouette of the sphere generated from the viewing position of the light source. the silhouette is simply made up of edges that consist of two vertices each. these edges are then extrude in the direction as shown by the broken arrows originating from the light source.

by extrudinig the silhouette edges, we are effectively creating the shadow volume. it should be noted at this point in time that shadow volume extrusion differs for different light sources. 对不同光源，其边挤出的体积是不同的。

for point light sources, the silhouette edges extrude exactly point for point. for infinite directional light sources, the silhouette edges extrude to a single point. we will go into the details of determing silhouette edges and the creation of the shadow volumes later.

the magnitude of the extrusion can be either finite or infinite. thus, implementations that extrude silhouette edges to inifinity are commonly known as infinite shadow volumes. 分为无限挤出和有限挤出。

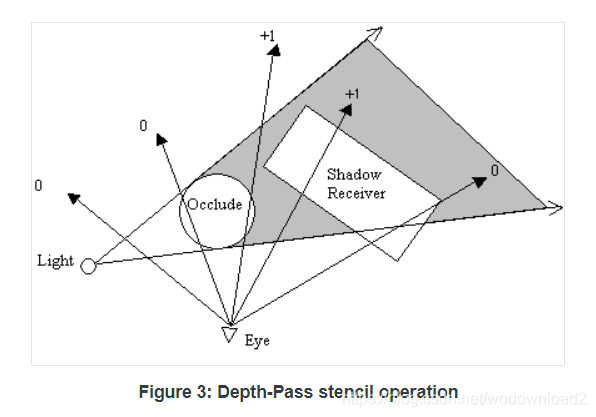
figure 3 shows the numerous possible viewing direction of a player in the scene. the numbers at the end of the arrows are the values left in the stencil buffer after rendering the shadow volume. fragments with non-zero stencil values are considered to be in shadow. the generation of the values in the stencil buffer is the result of the following stencil operations:

1. render front face of shadow volume. if depth test passes, increment stencil value, else does nothing. disable draw to frame and depth buffer.
2. render back face of shadow volume. if depth test passes, decrement stencil value, else does nothing. disable draw to fame and depth buffer.
   the above algorithm is also known as the depth-pass stencil shadow volume tenchnique since we manipulate the stencil values only when depth test passes. depth-pass is also commonly known as z-pass.

let us assume that we had already rendered the objects onto the frame buffer prior to the above stenciling operations… this means that the depth buffer would have been set with the correct values for depth testing or z-testing if u like.

the 2 leftmost ray originating from the eye position does not hit any part of the shadow volume (in gray), hence the resultant sentcil values is 0, which means that the fragment represented by this two rays are not in shadow. 下图的两个射线，最左边的两个射线不在阴影中

now lets trace the 3 ray from the the left. when we render the front face of the shadow volume, the depth test would pass and the stencil vlaue would be incremented to 1. when we render the back face of the shadow volume, the depth test would fail since the back face of the shadow volume is behind the occluder. thus the stencil vaue for the fragment represented by this ray remains at 1. this means that the fragment is in shadow since its stencil vaue is non-zero.

does the shadow volume counting work for multiple shadow volumes? yes it does.

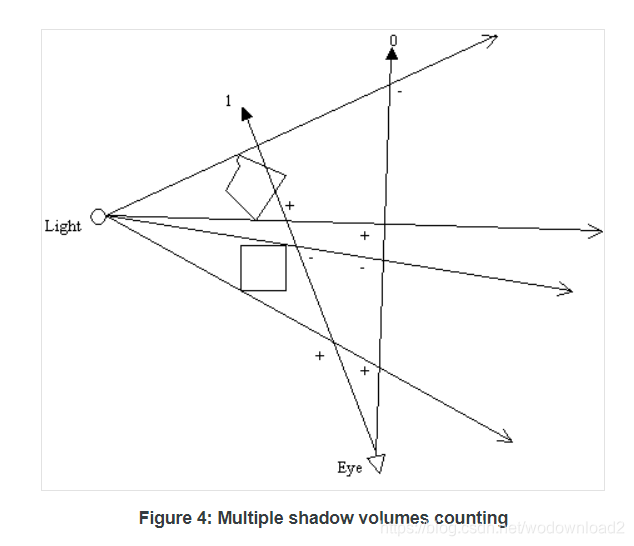
firgure 4 above shows that the counting using the stencil buffer will work even for multiple intersecting shadow volumes.

finite volume vs infinite volume.