含柯氏力的龙卷风优化算法(Tornado Optimizer with Coriolis Force, TOC)是一种受自然界龙卷风形成与演化机制启发的新型智能优化算法。自然界中,龙卷风凭借柯氏力的驱动与风暴系统的能量耦合,在复杂大气环流中完成从气流旋转到能量聚焦的剧烈转变,其从孕育、增强到消散的全周期过程,既展现出对环境能量的精准捕获,又蕴含着混沌中有序的动态平衡智慧。TOC 正是模拟龙卷风在大气运动中的三大核心行为特征:基于柯氏力的旋转增强机制、风暴系统能量汇聚的梯度搜索策略,以及从大范围气流扰动到局部能量聚焦的双阶段演化过程。这些特征被巧妙转化为可量化的数学算子 —— 旋转增强算子负责强化搜索方向的稳定性,而梯度汇聚算子则推动解空间的精准收敛,协同实现复杂优化问题中探索与开发的动态平衡。

该成果于2025年发表在计算机领域一区期刊Artificial Intelligence Review上,影响因子高达13.9,具有广泛的应用前景。
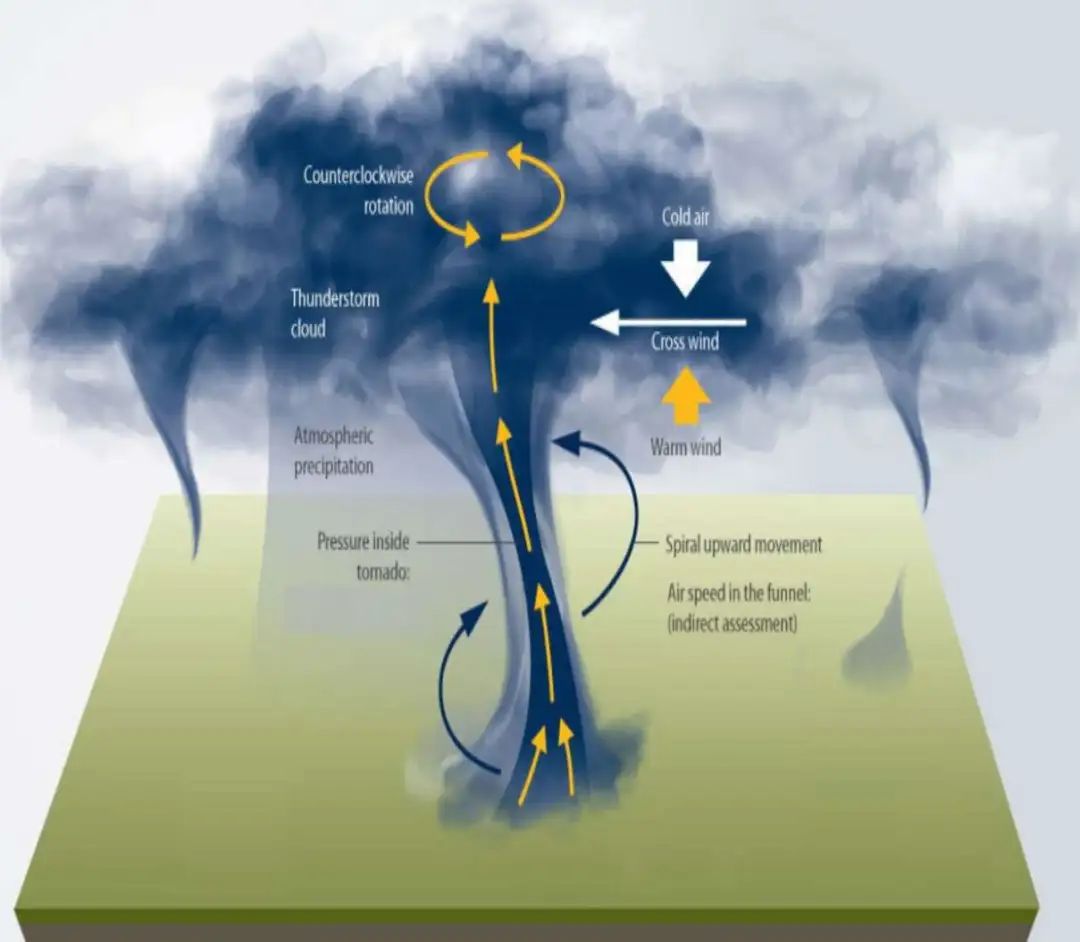
TOC优化算法的理念,源于对自然界中龙卷风形成与消散过程以及风暴和雷暴如何演变为龙卷风的观察。当风暴系统内的风速和风向发生变化时,这个周期便开始了。这会产生旋转效应,雷暴中的上升气流将其垂直倾斜。在这种情况下,通常会形成风暴。当风暴增强时,它往往会变成超级单体雷暴。换言之,一场强烈的雷暴会在大气中数英里高处形成一个旋转系统,这个系统会成为超级单体或雷暴云团。这些超级单体雷暴是独特的、孤立的云团,不属于风暴线的一部分。超级单体风暴是会不断旋转的风暴。当旋转的垂直气流柱与超级单体雷暴相遇时,风暴云可能会产生龙卷风。龙卷风形成过程的各个阶段可在下图观察到。

如下图所示,最初的漏斗云从雷暴云中生成,盘旋在地面上方。然后,如果条件有利(温度波动、风等),龙卷风就会成形并触及地面。最后,当条件开始变化时,漏斗云会变窄,并开始逐渐向云层上升。
1、代码原理
(1)种群初始化
如上所述,将生成 场风暴,因此需从整个种群中选出相应数量的候选个体。以下公式展示了 (即风暴种群)演变为龙卷风或雷暴的过程:
(2)风暴的形成
依据风暴演化的规模和强度,龙卷风与每一场雷暴均会吸收风暴。无论如何,在龙卷风与雷暴之间按比例分配风暴的最佳方法之一,是为二者采用成本函数(适应度函数)。因此,可演化为雷暴和/或龙卷风的风暴数量会发生变异。针对龙卷风与每一场雷暴的指定风暴,可通过以下数学公式进行评估:
其中,,且 表示与龙卷风相关的第 个雷暴的成本值。
其中, 表示取整运算符,,且 为可演化为指定雷暴或龙卷风的风暴数量。
(3)考虑科氏力的风暴速度
对于不需要沿直线运动的大尺度大气湍流,科氏力、离心力与压力梯度力之间形成三力平衡。据此,产生雷暴和龙卷风的梯度风暴速度可由以下公式确定:
其中, 表示规模为 的风暴种群的个体索引, 代表第 个风暴的新速度向量, 表示第 个风暴的当前速度向量, 指代 [0, 1] 范围内均匀分布的随机数, 为用于模拟风暴收敛行为的收缩因子。
其中, 表示风暴的加速度比率。
(4)风暴向龙卷风的演化
TOC优化算法实现了风暴向龙卷风的转化机制:当风暴达到特定演化条件时,将生成单个或多个龙卷风。该转化过程的数学模型如下式所示:
其中, 和 分别表示第 个风暴在 和 迭代时刻的下一时刻和当前时刻位置向量, 表示第 个龙卷风在 时刻迭代的当前位置向量, 表示风暴演化为龙卷风的过程与风暴随机形成之间的差异, 和 为随机变量,其定义如下所示:
其中, 是用于随机选择风暴的索引向量。
其中, 表示在区间 [0, 1] 上均匀分布的随机数, 为指数参数,其定义如下所示:
其中, 表示一个固定常数,其值为2.0,该数值是经过大量分析后确定的。
(5)风暴向雷暴的演化
如前所述,种群包含n个个体,其中n_t个被选为雷暴,n_o个被选为龙卷风。本研究中假设仅存在一个龙卷风。下图展示了风暴沿其接触线演化为特定雷暴的示意图。
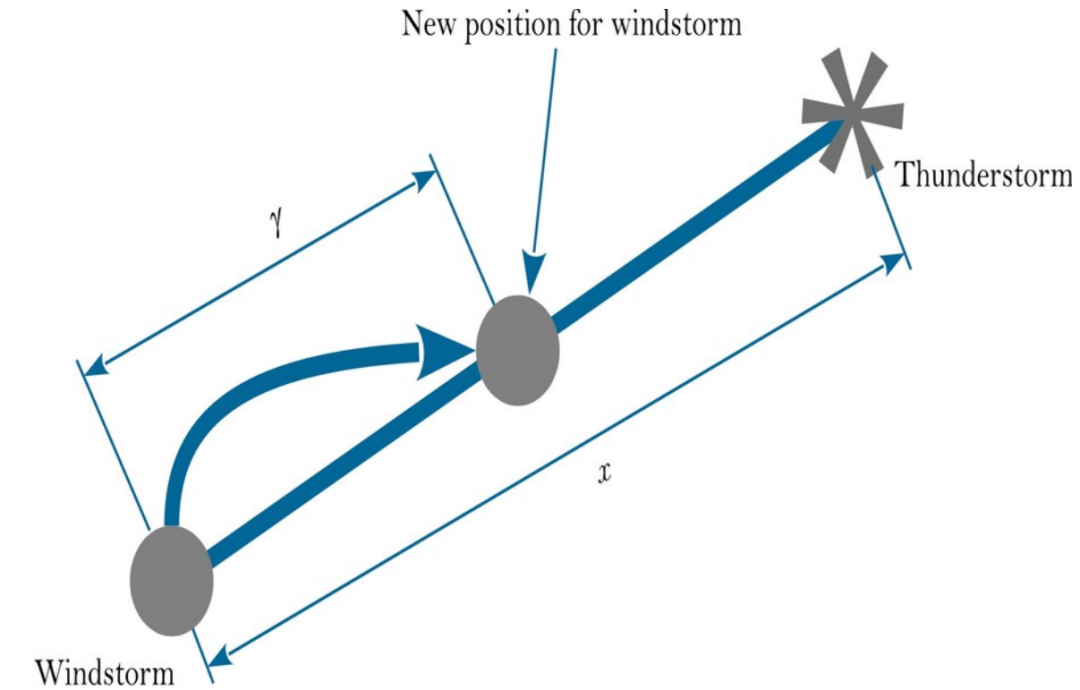
风暴与雷暴之间的距离γ可按公式进行随机修正:
其中,x表示风暴与雷暴之间的当前距离,0.5 < ρ < 2(ρ的最优值可能为2)。γ服从0到之间的随机数,该随机数采用均匀分布或其他合理分布。当ρ > 0.5时,风暴可沿多个方向向雷暴演化。此原理同样适用于解释雷暴如何演化为龙卷风。本质上,为平衡TOC算法的探索与开发阶段,风暴向雷暴的演化过程可模拟如下:
其中, 和 分别表示将演化为雷暴的风暴在 和 迭代时刻的下一时刻与当前时刻位置向量, 表示第 个雷暴在 时刻迭代的当前位置向量, 为 [0,1] 范围内均匀分布的随机数。
(6)雷暴向龙卷风的演化
在所提出优化算法的探索与开发阶段,雷暴演化为龙卷风过程中的新位置可按以下方式模拟:
其中, 表示随机索引 处龙卷风的位置向量。 为随机选择雷暴的索引向量,其定义方式如下式所示:
其中, 是 [0, 1] 范围内均匀分布的随机数。
当前雷暴将统辖所有早期风暴。类似转换机制也适用于雷暴与龙卷风之间、以及风暴与龙卷风之间的状态转换。在此过程中,进化中的雷暴将获得龙卷风属性,而被替代的龙卷风则转化为携带自有风暴群的新雷暴,这些风暴将沿其方向定向演化。因此,与原雷暴(现为新龙卷风)关联的风暴,将直接向该龙卷风演化。下图展示了该优化算法中风暴与雷暴的交换机制。
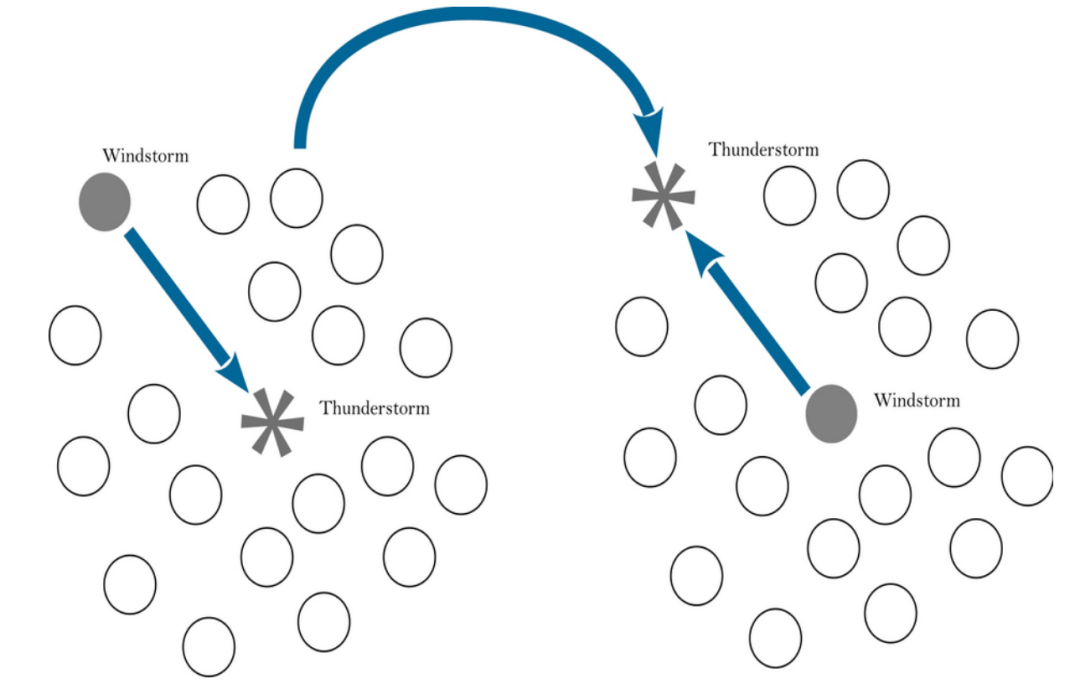
如下图所示,优化过程中球体、星号与圆点分别代表风暴、雷暴与龙卷风。白色空心标记表示风暴与雷沙的迁移轨迹。
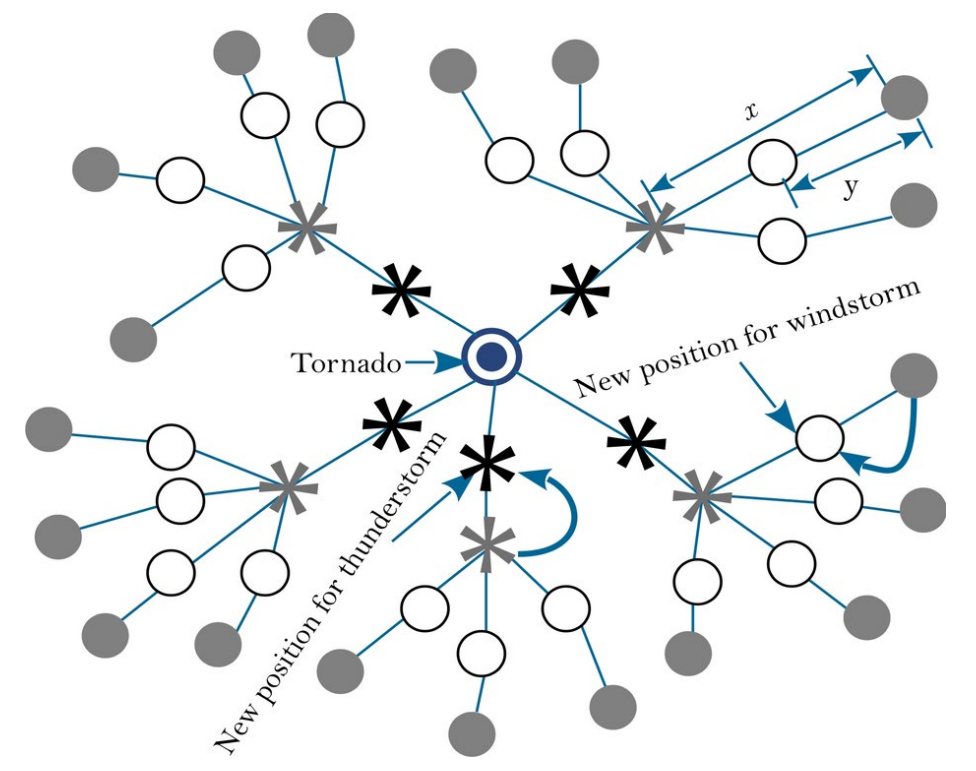
TOC优化算法的流程图如下所示:

2、结果展示
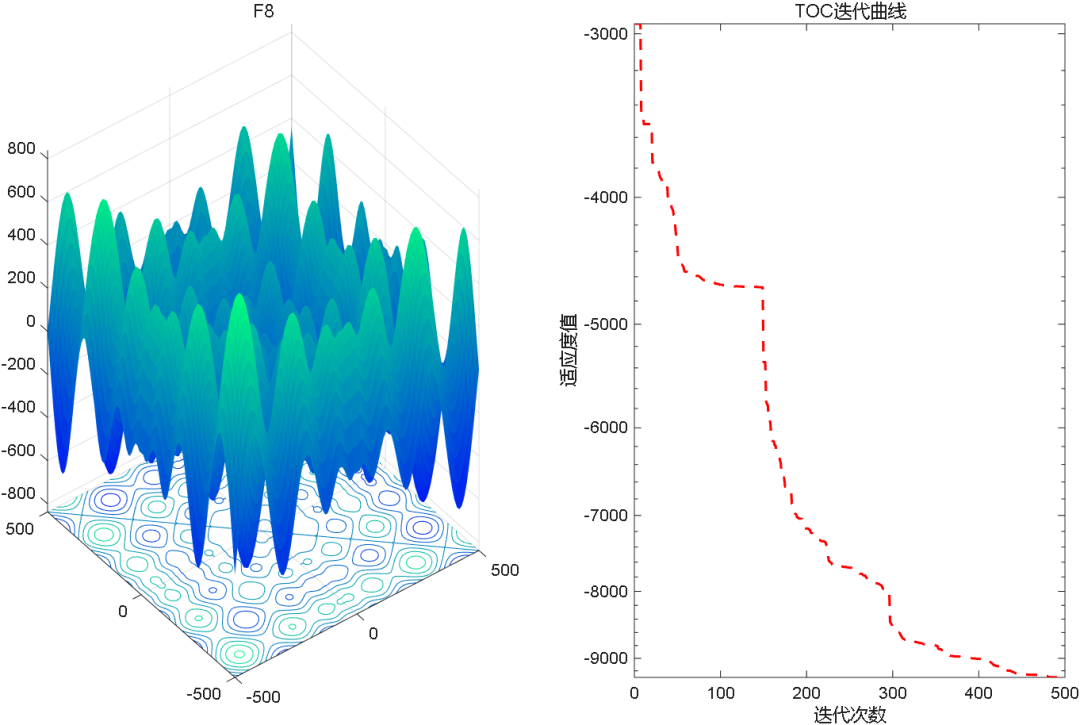
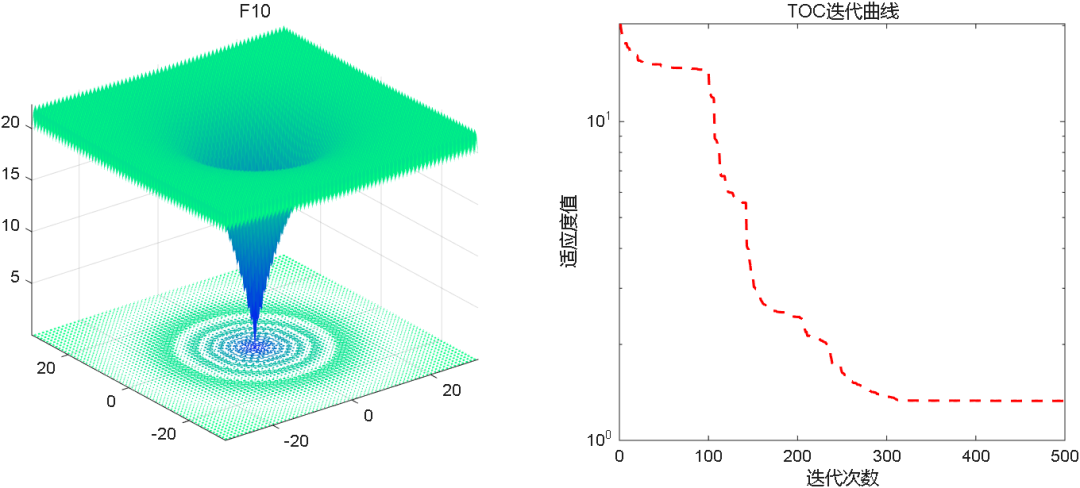
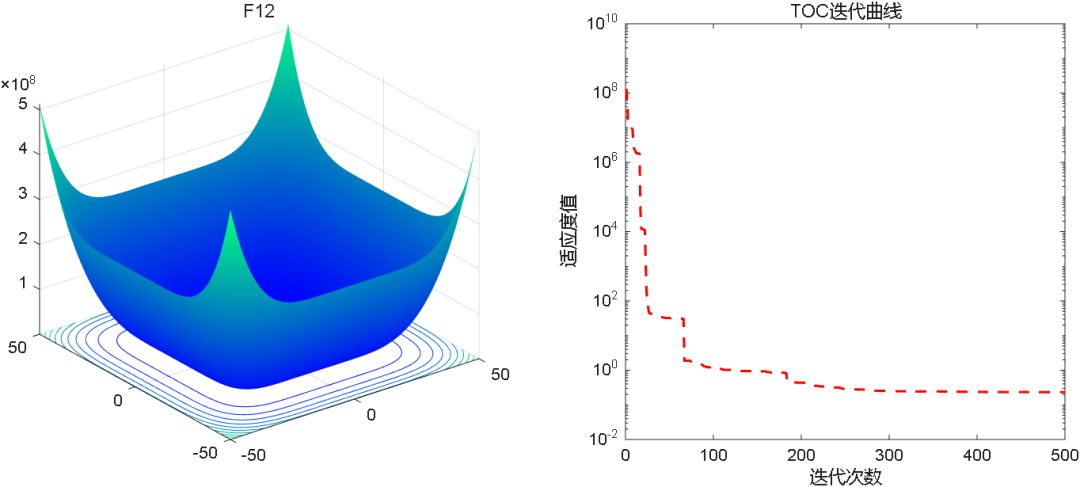
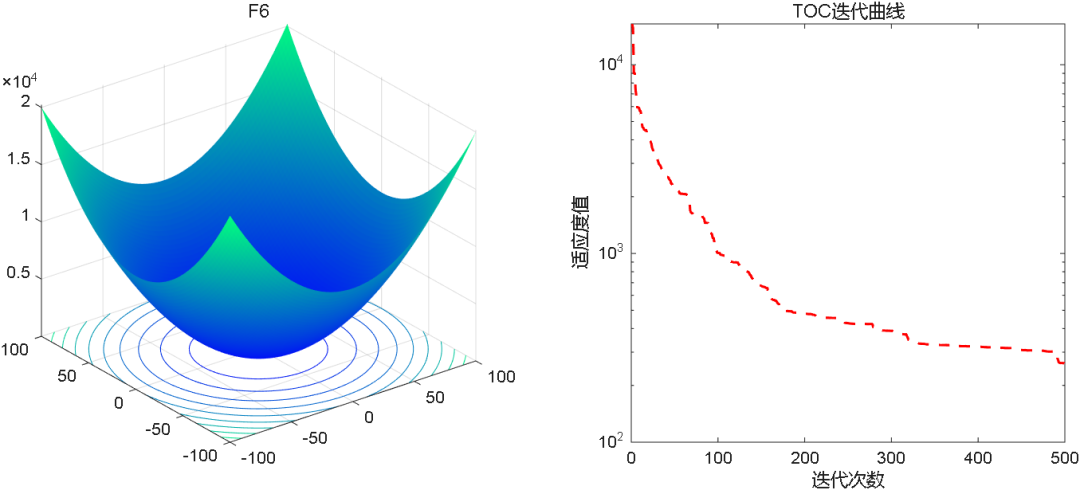
3、MATLAB核心代码
%% 淘个代码 %%
% 微信公众号搜索:淘个代码,获取更多代码
% 含柯氏力的龙卷风优化算法(Tornado Optimizer with Coriolis Force, TOC)
function [TornadoCost,Tornadoposition,ccurve]=TOC(n,max_it,lb,ub,dim,fobj,nto,nt)
%% Convergence curve
ccurve=zeros(1,max_it);
%% Generate initial population for the Tornado Optimizer with Coriolis force (TOC)
% Create initial population for Tornado, thunderstorms, and windstorms, and initialize the positions of population
y=initialization(n,dim,ub,lb);
% Evaluate the fitness of initial population for Tornado, thunderstorms, and windstorms
fit = zeros(size(y,1),1);
for i=1:size(y,1)
fit(i,1)=fobj(y(i,:));
end
[~,index]=sort(fit) ;
%% Forming Windstorms, Thunderstorms, and Tornado of the Tornado Optimizer with Coriolis force (TOC)
% nto: Number of thunderstorms and tornadoes
% Nt : Number of thunderstorms
% To: Number of tornadoes
% nw: number of windstorms
To= nto - nt;% Tornadoes
nw=n-nto; % Windstorms
%================ Forming and evaluating the population of the Tornadoes ================
Tornadoposition=y(index(1:To),:) ; %
TornadoCost=fit(index(1:To));
%================ Forming and evaluating the population of the Thunderstorms ================
Thunderstormsposition(1:nto-1,:)=y(index(2:nto),:);
ThunderstormsCost(1:nto-1)=fit(index(2:nto));
bThunderstormsCost = ThunderstormsCost;
gThunderstormsCost=zeros(1,nto-1);
[~,ind]=min(ThunderstormsCost);
bThunderstormsposition = Thunderstormsposition; % Initial best Thunderstorms position
gThunderstormsCost = Thunderstormsposition(ind,:); % Initial global Thunderstorms position
%================ Forming and evaluating the population of the Windstorms ================
Windstormsposition(1:nw,:)=y(index(nto+1:nto+nw),:) ;
WindstormsCost(1:nw)=fit(index(nto+1:nto+nw)) ;
gWindstormsposition=zeros(1,nw);
bWindstormsCost = WindstormsCost;
[~,ind]=min(WindstormsCost);
bWindstormsposition = Windstormsposition; % % Initial best windstorms position (Update the best positions of windstorms)
gWindstormsposition = Windstormsposition(ind,:); % Initial global windstorms position
%% Velcity term of TOC
vel_storm = 0.1*Windstormsposition; % Velocity of windstorms
%% Designate windstorms to thunderstorms and Tornadoes
nwindstorms=1:nw;
nwindstorms=nwindstorms(sort(randperm(nw,nto)));
% Combining windstorms to tornado
nWT=diff(nwindstorms)';
nWT(end+1)= nw-sum(nWT);
% nWT1=sort(nWT1,'descend');
nWT1 = nWT(1);
% Combining windstorms to thunderstorms
nWH=nWT(2:end);
%% Parameter setting s for TOC
b_r=100000;
fdelta=[-1,1];
%% Key functions of Tornado Optimizer with Coriolis force (TOC)
chi=4.10;
eta=2/abs(2-chi-sqrt(chi^2-4*chi)) ;
%% ================ Main Loop for TOC ================
disp('================ Tornado Optimizer with Coriolis force (TOC) ================ ');
t=1;
while t<=max_it
%% Key adaptive functions (Adaptive parameters) of TOC
nu =(0.1*exp(-0.1*(t/max_it)^0.1))^16;
mu = 0.5 + rand/2;
ay=(max_it-(t^2/max_it))/max_it ;
Rl = 2/(1+exp((-t+max_it/2)/2)) ;
Rr = -2/(1+exp((-t+max_it/2)/2)) ;
%% Evolution of windstorms to Tornadoes
% Update velocity
for i=1:nw
for j = 1:dim
if rand > 0.5
delta1=fdelta(ceil(2*rand()));
zeta=ceil((To).*rand(1,To))'; %
wmin=1; wmax=4.0; rr=wmin+rand()*(wmax-wmin);
wr= (((2*rand()) - (1*rand()+rand()))/rr);
c=b_r*delta1*wr;
omega = 0.7292115E-04;
% w_r = sin(-1 + 2.*rand(1,1));
f= 2*omega*sin(-1 + 2.*rand(1,1));
phi(i,j) = Tornadoposition(zeta,j) - Windstormsposition(i,j);
if sign(Rl)>=0
if sign(phi(i,j))>=0
phi(i,j) = -phi(i,j);
end
end
CFl =(((f^2*Rl^2)/4) -Rl* 1 *phi(i,j));
if sign(CFl)< 0
CFl= -CFl;
end
vel_storm(i,j)= eta* (mu*vel_storm(i,j) - c* (f*Rl)/2 +(sqrt(CFl)));
else
delta1=fdelta(ceil(2*rand()));
zeta=ceil((To).*rand(1,To))'; %
rmin=1; rmax=4.0; rr=rmin+rand()*(rmax-rmin);
wr= (((2*rand()) - (1*rand()+rand()))/rr);
c=b_r*delta1*wr;
phi(i,j) = Tornadoposition (zeta,j)-Windstormsposition(i,j);
if sign(Rr)<=0
if sign(phi(i,j))<=0
phi(i,j) = -phi(i,j);
end
end
omega =0.7292115E-04;% s�1
% w_r = sin(-1 + 2.*rand(1,1));
f= 2*omega*sin(-1 + 2.*rand(1,1));
CFr =(((f^2*Rr^2)/4) -Rr* 1 *phi(i,j));
if sign(CFr)<0
CFr= -CFr;
end
vel_storm(i,j)= eta *(mu* vel_storm(i,j) - c* (f*Rr)/2 +(sqrt(CFr))) ;
end
end
end
%% %% Exploration - Evolution of windstorms to Tornadoes
for i=1:nWT1
rand_index = floor((nWT1).*rand(1,nWT1))+1;
rand_w = Windstormsposition(rand_index, :);
alpha=abs(2*ay*rand-1*rand) ;
Windstormsposition(i,:)=Windstormsposition(i,:)+2*alpha*(Tornadoposition - rand_w(i,:)) + vel_storm(i,:);
%
ub_=Windstormsposition(i,:)>ub; lb_=Windstormsposition(i,:)<lb;
Windstormsposition(i,:)=(Windstormsposition(i,:).*(~(ub_+lb_)))+ub.*ub_+lb.*lb_;
WindstormsCost (i)=fobj(Windstormsposition(i,:));
%%% Finding out the best positions
if WindstormsCost(i)<bWindstormsCost(i)
bWindstormsposition(i,:)=Windstormsposition(i,:) ; % Best solutions
bWindstormsCost(i)=WindstormsCost(i); % Best cost
end
end
[minTornadoCost,in]=min(bWindstormsCost); % finding out the best Pos
if (minTornadoCost<TornadoCost)
TornadoCost=minTornadoCost;
Tornadoposition = bWindstormsposition(in,:); % Update the global best positions
end
%% ================ Exploitation - Evolution of windstorms to thunderstorms ================
%% ================ Combining windstorms together to form thunderstorms ================
for i=1:nt
for j=1:nWH(i)
rand_index = floor((nt).*rand(nt))+1;
rand_w = Windstormsposition(rand_index, :);
c1=abs(2*ay*rand-1*ay);
c2=abs(ay - 2*ay*rand);
Windstormsposition((j+sum(nWT(1:i))),:)=Windstormsposition((j+sum(nWT(1:i))),:)+2*rand*(Thunderstormsposition(i,:)-Windstormsposition((j+sum(nWT(1:i))),:))+...
+ 2*rand*(Tornadoposition (1,:)-Windstormsposition((j+sum(nWT(1:i))),:));
ub_=Windstormsposition((j+sum(nWT(1:i))),:)>ub; lb_=Windstormsposition((j+sum(nWT(1:i))),:)<lb;
Windstormsposition((j+sum(nWT(1:i))),:)=(Windstormsposition((j+sum(nWT(1:i))),:).*(~(ub_+lb_)))+ub.*ub_+lb.*lb_;
WindstormsCost((j+sum(nWT(1:i))))=fobj(Windstormsposition((j+sum(nWT(1:i))),:));
if WindstormsCost((j+sum(nWT(1:i))))<ThunderstormsCost(i)
bThunderstormsposition(i,:) =Windstormsposition((j+sum(nWT(1:i))),:);
Thunderstormsposition(i,:)=Windstormsposition((j+sum(nWT(1:i))),:);
ThunderstormsCost(i)=WindstormsCost((j+sum(nWT(1:i))));
end
end
end
%
[minTornadoCost, in]=min(ThunderstormsCost); % finding out the best Pos
if (minTornadoCost<TornadoCost)
TornadoCost=minTornadoCost;
Tornadoposition = bThunderstormsposition(in,:); % Update the global best positions
end
%% ================ Evolution of thunderstorms to tornado ================
for i=1:nt
zeta=ceil((To).*rand(1,To)); %
alpha=abs(2*ay*rand-1*rand) ;
p = floor((nt).*rand(1,nt))+1;
rand_w = Thunderstormsposition(p, :);
Thunderstormsposition(i,:)=Thunderstormsposition(i,:)+2.*alpha*(Thunderstormsposition(i,:) - Tornadoposition(zeta,:))+...
+2.*alpha*(rand_w(i,:) - Thunderstormsposition(i,:));
ub_=Thunderstormsposition(i,:)>ub; lb_=Thunderstormsposition(i,:)<lb;
Thunderstormsposition(i,:)=(Thunderstormsposition(i,:).*(~(ub_+lb_)))+ub.*ub_+lb.*lb_;
ThunderstormsCost(i) =fobj(Thunderstormsposition(i,:));
if ThunderstormsCost(i)<bThunderstormsCost(i)
bThunderstormsposition(i,:) =Thunderstormsposition(i,:);
bThunderstormsCost(i) =ThunderstormsCost(i);
end
end
[minTornadoCost,in]=min(bThunderstormsCost); % finding out the best Pos
if (minTornadoCost<TornadoCost)
TornadoCost=minTornadoCost;
Tornadoposition = bThunderstormsposition(in,:); % Update the global best positions
end
%% ================ Random formation of windstorms, tornadoes and thunderstorms ================
% Check windstorms formation for windstorms and tornadoes
for i=1:nWT1
if ((norm(Windstormsposition(i,:)-Tornadoposition)<nu))
delta2=fdelta(floor(2*rand()+1));
Windstormsposition(i,:)= Windstormsposition(i,:) - (2*ay*(rand*(lb-ub) - lb))*delta2;
end
end
% Check windstorms formation for windstorms and thunderstorms
for i=1:nt
if ((norm(Windstormsposition(i,:)-Thunderstormsposition(i,:))<nu))
for j=1:nWH(i)
delta2=fdelta(floor(2*rand()+1)) ;
Windstormsposition((j+ sum(nWT(1:i))),:)= Windstormsposition((j+ sum(nWT(1:i))),:) - (2*ay*(rand*(lb-ub) - lb))*delta2;
end
end
end
%% Results and Plot
ccurve(t)=TornadoCost;
%{
if t>2
line([t-1 t], [ccurve(t-1) ccurve(t)],'Color','b');
title({'Convergence characteristic curve'},'interpreter','latex','FontName','Times','fontsize',12);
xlabel('Iteration');
ylabel('Best score obtained so far');
drawnow
end
%}
t=t+1;
end
end参考文献
[1] Braik M, Al-Hiary H, Alzoubi H, et al. Tornado optimizer with Coriolis force: a novel bio-inspired meta-heuristic algorithm for solving engineering problems[J]. Artificial Intelligence Review, 2025, 58(4): 123.
完整代码获取
后台回复关键词:
TGDM869
获取更多代码:

或者复制链接跳转:https://docs.qq.com/sheet/DU3NjYkF5TWdFUnpu




















 2344
2344

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










