2025年优化算法——梦境优化算法

注：该算法已按照智能优化算法APP标准格式进行整改，可直接集成到APP中，方便大家与自己的算法进行对比。

梦境优化算法（Dream Optimization Algorithm, DOA）是一种受到人类梦境机制启发的智能优化方法。梦境，这一神秘又熟悉的心理现象，不仅承载着模糊的记忆片段，还展现出遗忘、重构与逻辑组织的能力——这些正与智能优化中的搜索、更新与自适应过程高度契合。受此启发，研究人员提出DOA算法，模拟梦境的三大核心机制：基础记忆的保留、探索性遗忘与补充机制，以及梦境共享传播策略。这些机制被精炼为优化搜索中的数学操作，赋予DOA算法在全局探索与局部开发间更出色的平衡能力。

该成果于2025年最新发表在工程技术领域一区期刊Computer Methods in Applied Mechanics and Engineering上，目前被引用17次。

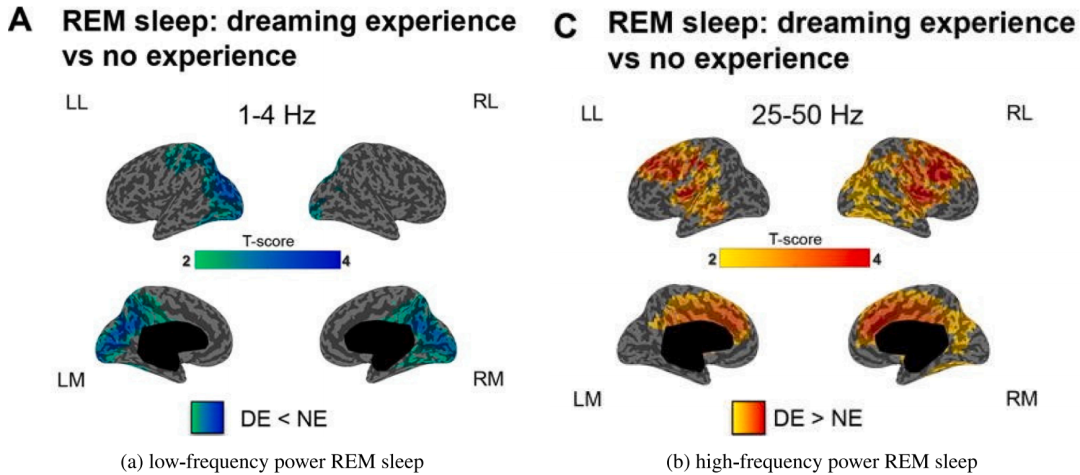
梦境主要源自一种特定的睡眠阶段，即快速眼动（REM）睡眠阶段，该阶段通常在入睡约90分钟后开始。在这一阶段，眼球会快速移动，由于该阶段与梦境的发生密切相关，因此被称为REM睡眠期。下图展示了REM睡眠中伴随梦境体验与无梦体验时，脑电中低频与高频活动功率的差异。可以明显看到，在伴随梦境体验的REM阶段，低频脑波的功率降低，而高频脑波的功率增强，表明梦境体验期间大脑神经激活程度更高。

1、算法原理

（1）初始化

与其他元启发式算法类似，在初始化阶段，DOA首先在搜索空间内随机生成一个初始种群，从而启动算法的优化过程。用于获取初始种群的公式如下所示：

其中，   表示个体数量，即种群规模；  表示种群中的第 个个体；  与 分别表示搜索空间的下界与上界；  是一个维度为 的向量，其每一维均为 到  之间的随机数；最终得到的初始种群可表示为：

其中，   表示第   个个体在第   个维度上的位置，   表示优化问题的维度。

（2）探索阶段

在探索阶段（迭代次数从   到  ），首先根据记忆能力的差异将种群划分为   个子群体，各组内个体的更新方式如下：每次迭代被视为一次“做梦”行为，通过不断执行该行为来寻求最优解与最优值。在每一次“梦境”开始前，各组中的所有个体都会被展示上一轮迭代中的最优个体。

由于个体在梦境中会随机遗忘部分信息，因此仅在这些遗忘维度上更新位置。不同组的记忆能力差异，体现在各自遗忘的维度数量不同，分别用参数   表示。因此，每个个体首先将其位置重置为所属组在过往迭代中的最优个体的位置，然后从总维度   中随机选取   个维度（记为  ），并仅在这些维度上进行位置更新，其中   表示组号。

在每轮迭代中，个体的更新按序从第   个到第   个依次进行。具体的更新方法如下。

记忆策略：首先，根据基础记忆策略，对于第   组中的个体而言，在进入梦境前可以记住其所在组中最优个体的位置，并将自身位置信息重置为该最优个体的位置：

其中，   表示第 个个体在第 次迭代时的位置，  表示第 组在第  次迭代时的最优个体。

遗忘与补充策略：遗忘与补充策略结合了全局搜索与局部搜索能力。该策略遵循记忆策略，允许个体在遗忘维度中遗忘并自我组织位置信息。更新公式如下：

其中，   表示第 次迭代中第 个个体在第 维的位置；  表示第 次迭代中第 组中表现最优个体在第 维的位置；  和 分别是第 维搜索空间的下界和上界；  是取值在 0 到 1 之间的随机数；  是当前迭代次数，  是最大迭代次数，   是探索阶段的最大迭代次数。

共享梦境策略：DOA中的共享梦境策略增强了逃离局部最优的能力。该策略与遗忘与补充策略并行运行，遵循记忆策略，允许个体在遗忘维度中随机获取其他个体的位置位置信息。更新公式如下：

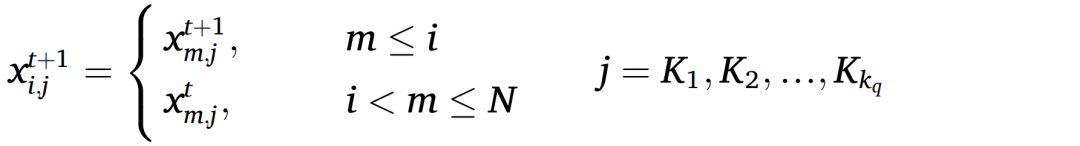
其中，   表示第 次迭代中第 个个体在第 维的位置；  是在每个维度更新时从区间  中随机选取的自然数。

（3）开发阶段

在开发阶段（迭代次数从   到  ），不再进行分组。在每次做梦之前，会将上一迭代中整个人群的最佳梦境（即上一迭代中表现最优的个体）展示给整个种群。随后，更新每个个体在遗忘维度上的位置。种群中所有个体的遗忘维度数量相同，记为  。从   个维度中随机选择   个遗忘维度，记为  ，并对这些维度的位置进行更新。

记忆策略的更新过程如下：

其中，   表示第   次迭代中的第   个个体，   表示第   次迭代中整个人群的最优个体。

遗忘与补充策略的更新过程如下：

其中，   表示第 次迭代中第 个个体在第 维的位置；  表示第 次迭代中整个人群在第 维上的最优个体位置；  和 分别是第 维搜索空间的下界和上界；  是取值在 0 到 1 之间的随机数；  是当前迭代次数，   是算法的最大迭代次数。

DOA优化算法的伪代码如下所示：

2、结果展示

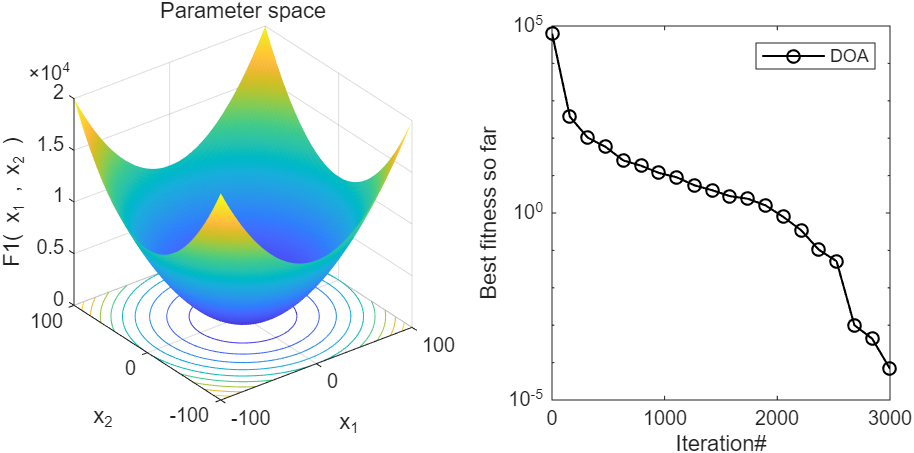
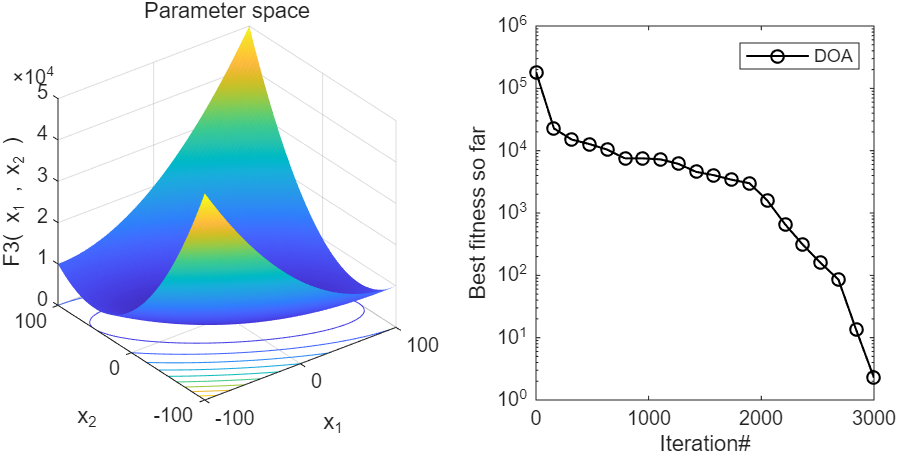
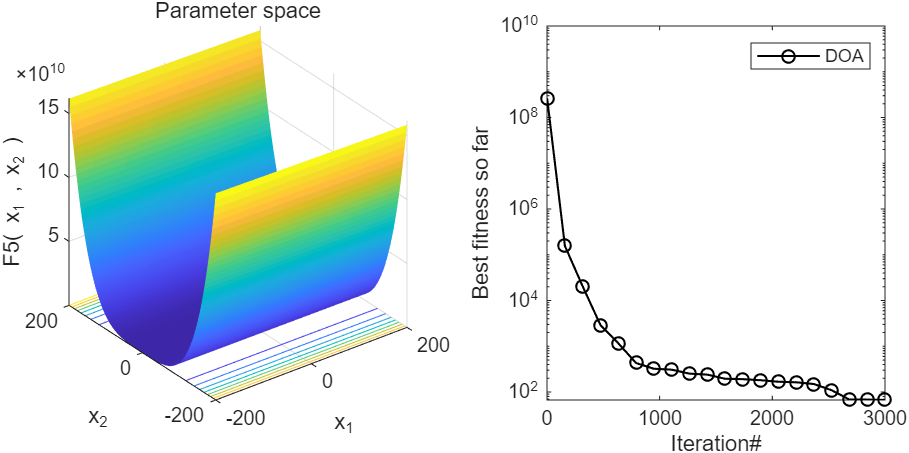
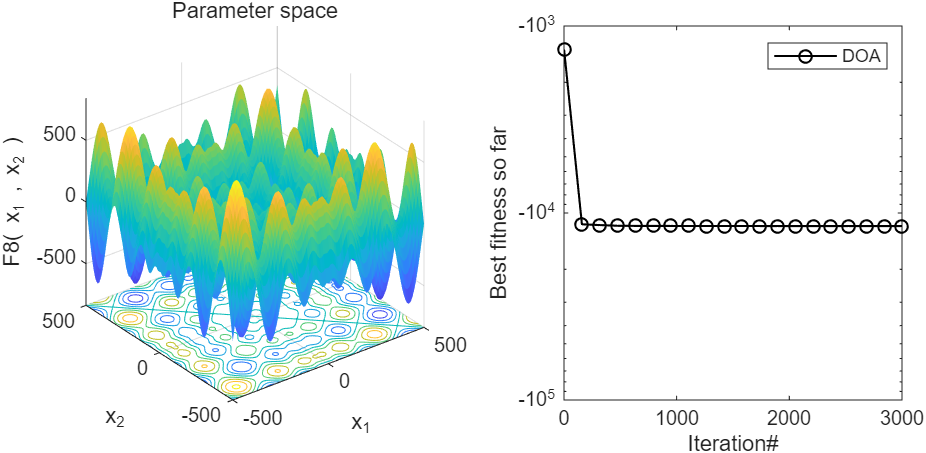
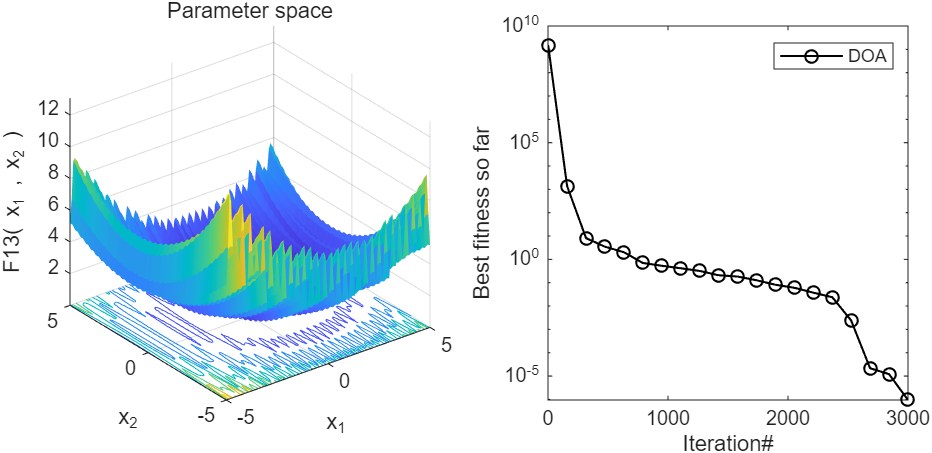
3、MATLAB核心代码

function [fbest,sbest,fbest_history] = DOA(pop,T,lb,ub,D,fobj)%pop stands for population size%T represents the maximum number of population iteration%lb represents the lower bound of the search space%ub represents the upper bound of the search space%D represents the dimension of the problem%fobj represents the objective functionlb=lb.*ones(1,D);   ub=ub.*ones(1,D);                            %Ensure that the dimensions of the upper and lower bounds match the dimensionality of the problemx =initialization(pop,D,ub,lb);              %Initialize the populationSELECT=1:pop;                                      sbest=ones(1,D);                             %sbest is the current optimal solutionsbestd=ones(5,D);                            %sbestd represents the current optimal solution for each of the 5 groupsfbest=inf;                                   %fbest is the current optimal valuefbestd=ones(5,1);                            %fbestd represents the current optimal value for each of the 5 groupsfbest_history=ones(1,T);                     %fbest_history is a vector composed of the best values of each generationfor i = 1:5      fbestd(i)=fbest;end   
for i=1:(9*T/10)                                               %Exploration phase      for m=1:5                                                %Divide into 5 groups                k=randi([ceil(D/8/m),ceil(D/3/m)]);                     for j=(((m-1)/5*pop)+1) : (m/5*pop)                                      if (fobj(x(j,:)) <fbestd(m))                      sbestd(m,:)=x(j,:);                                               fbestd(m)=fobj(x(j,:));                  %Update the optimal value and solution for each group                     end         end          for j=(((m-1)/5*pop)+1) : (m/5*pop)           x(j,:)=sbestd(m,:);                                  %Memory strategy           in=randperm(D,k);                   if rand<0.9               for h=1:k                   x(j,in(h))=x(j,in(h))+(rand*(ub(in(h))-lb(in(h)))+lb(in(h)))*(cos((1*i+T/10)*pi/T)+1)/2;      %Forgetting and supplementation strategy                if (x(j,in(h))>ub(in(h))) | (x(j,in(h))<lb(in(h)))                       if D>15                                      %The boundary handling method when the problem dimensionality>15                     select=SELECT;                          select(j)=[];                     sel=select(randi(pop-1));                                                  x(j,in(h))=x(sel,in(h));                     else                                          %The boundary handling method when the problem dimensionality<=15                     x(j,in(h))=rand*(ub(in(h))-lb(in(h)))+lb(in(h));                                    end                   end               end            else               for h=1:k                                          x(j,in(h))=x(randi(pop),in(h));                                                     end             end          end                 if (fbestd(m)<fbest)            %Update the optimal value and solution for the entire population               fbest=fbestd(m);               sbest=sbestd(m,:);            end      end                                               fbest_history(i)=fbest;                                                                  endfor i=((9*T/10)+1):T                        %Exploitation phase      for p=1 : pop                               if (fobj(x(p,:)) <fbest)          %Update the optimal value and solution for the entire population          sbest=x(p,:);          fbest=fobj(x(p,:));          end                                                                                                   end                                   for j=1:pop        fitness(j,:)=fobj(x(j,:));        km=max(2,ceil(D/3));        k=randi([2,km]);        x(j,:)=sbest;        in=randperm(D,k);         for h=1:k            x(j,in(h))=x(j,in(h))+(rand*(ub(in(h))-lb(in(h)))+lb(in(h)))*(cos((i)*pi/T)+1)/2;     %Forgetting and supplementation strategy                          if (x(j,in(h))>ub(in(h))) | (x(j,in(h))<lb(in(h)))                   if D>15                                      %The boundary handling method when the problem dimensionality>15                select=SELECT;                     select(j)=[];                sel=select(randi(pop-1));                                             x(j,in(h))=x(sel,in(h));                 else                                          %The boundary handling method when the problem dimensionality<=15                   x(j,in(h))=rand*(ub(in(h))-lb(in(h)))+lb(in(h));                                end              end        end      endfbest_history(i)=fbest;                                                                  end          end%微信公众号搜索：淘个代码，获取更多免费代码%禁止倒卖转售，违者必究！！！！！%唯一官方店铺：https://mbd.pub/o/author-amqYmHBs/work%代码清单：https://docs.qq.com/sheet/DU3NjYkF5TWdFUnpu

参考文献

[1] Lang Y, Gao Y. Dream Optimization Algorithm (DOA): A novel metaheuristic optimization algorithm inspired by human dreams and its applications to real-world engineering problems[J]. Computer Methods in Applied Mechanics and Engineering, 2025, 436: 117718.

完整代码获取

后台回复关键词：

TGDM876

---

获取更多代码：

或者复制链接跳转：https://docs.qq.com/sheet/DU3NjYkF5TWdFUnpu