2025年优化算法——吕佩尔狐优化算法

原创于 2025-07-11 10:10:00 发布 · 685 阅读

CC 4.0 BY-SA版权

注：该算法已按照智能优化算法APP标准格式进行整改，可直接集成到APP中，方便大家与自己的算法进行对比。

吕佩尔狐优化算法（Rüppell’s Fox Optimizer, RFO）是一种受沙漠生存专家——吕佩尔狐智能觅食行为启发的新型群体智能优化方法。这种在严酷环境中依赖260°广角视觉与150°可旋听觉的狐狸，具备昼夜协同觅食、高效猎物定位与隐秘行动等复杂能力。科研人员模拟吕佩尔狐的三大关键生存策略：感知驱动的猎物搜索、认知调节的探索-开发平衡机制，以及动态多源协作觅食行为。这些策略被抽象为数学模型，构成RFO核心算法框架，兼顾全局搜索与局部开发。RFO在多个基准测试与工程约束优化问题中展现出卓越性能，在收敛速度与稳定性方面均优于多种先进算法，展示出其强大的适应性与实际应用潜力。

该成果于2025年最新发表在计算机领域期刊Cluster Computing期刊上，具有出色的应用前景。

吕佩尔狐（Rüppell’s Fox），又称吕佩尔沙狐，主要分布于中东、西南亚等地区广袤的沙漠。它们属于杂食性动物，饮食结构极为多样，几乎可食用所有能够获取的资源，且具备高度的社会性与灵活性。

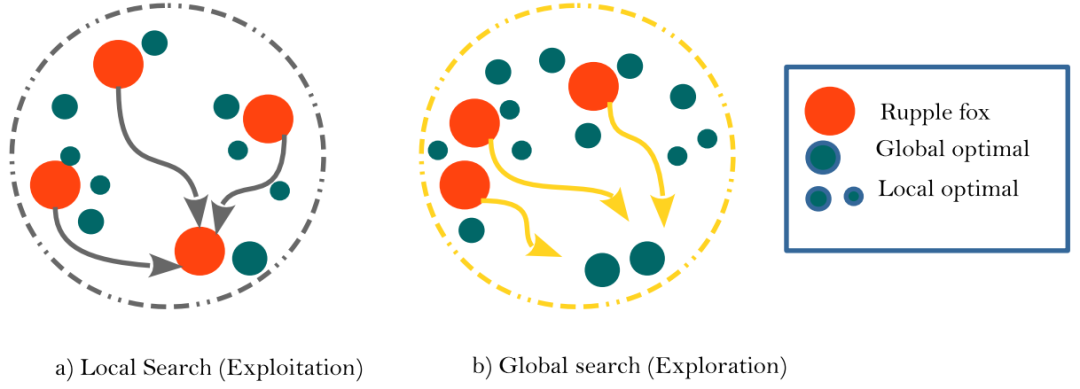
在狩猎过程中，吕佩尔狐会利用其异常敏锐的听觉、嗅觉和视觉不断扫描搜索空间以寻找猎物。它们是一类出色的猎手，具备高度协调的感知系统，能够精准解读周围环境，并据此做出快速反应，从而成功捕获猎物。吕佩尔狐在白天、夜晚、以及黎明与黄昏等时段均保持活跃，如下图所示。它们通常独自狩猎，在领地范围内悄然巡游，不断搜寻食物，并偏好在较大的区域内活动。

吕佩尔狐拥有极为灵敏的嗅觉，其鼻部对气味的感知能力使它们能够探测到深埋于地下的动物尸体。这种高度发达的嗅觉不仅用于狩猎，还被广泛用于个体间的交流——气味在群体中具有重要的社会功能，可用于识别个体身份、划定领地边界等。因此，吕佩尔狐在许多情况下仅凭气味就能准确找到猎物。如下图所示，吕佩尔狐可借助其听觉、视觉与嗅觉的协同作用，在林地的草丛与树木间灵活地搜索猎物。

1 算法原理详解

（1）数学模型与算法

由于RFO是一种基于种群的算法，其优化过程首先通过在搜索空间中随机生成一组初始解来启动，以求解目标优化问题。在维搜索空间中，种群规模为的吕佩尔狐种群中的每一个位置，均代表一个潜在的解，其可表示为一个的数组，形式如下：

其中，表示特定优化问题的决策变量个数，表示所有吕佩尔狐在搜索空间中的位置集合，表示第个吕佩尔狐在第个维度上的位置。

（2）视觉搜索

在此情境下，吕佩尔狐需在搜索空间内随机漫游以寻找猎物。其位置随着运动行为以及猎物位置的变化而动态调整。该行为可用公式进行建模：

其中，表示种群中第只吕佩尔狐的索引，表示第只吕佩尔狐在第次迭代中的位置，表示迄今为止所有吕佩尔狐在第次迭代中获得的全局最优位置向量，代表第只吕佩尔狐在第步的当前位置向量，是范围在之间的随机值，用于模拟昼夜交替，是均匀生成的区间随机数。

其中，表示向下取整函数，rand1 和 rand2 是在区间内均匀生成的随机数。

其中，表示在第次迭代中，第个已知的最佳位置向量，该位置为吕佩尔狐种群所熟知；表示吕佩尔狐根据以下公式随机到达该最佳位置：

其中，表示向上取整函数，rand(1, n) 表示在区间内生成的维度为的随机向量。

其中，和分别表示当前迭代次数和最大迭代次数，参数隐式体现了吕佩尔狐的视觉感知能力，且该能力随着迭代次数的增加逐渐增强，模拟狐狸逐渐靠近猎物的过程。该函数随迭代路径的变化如下图所示。

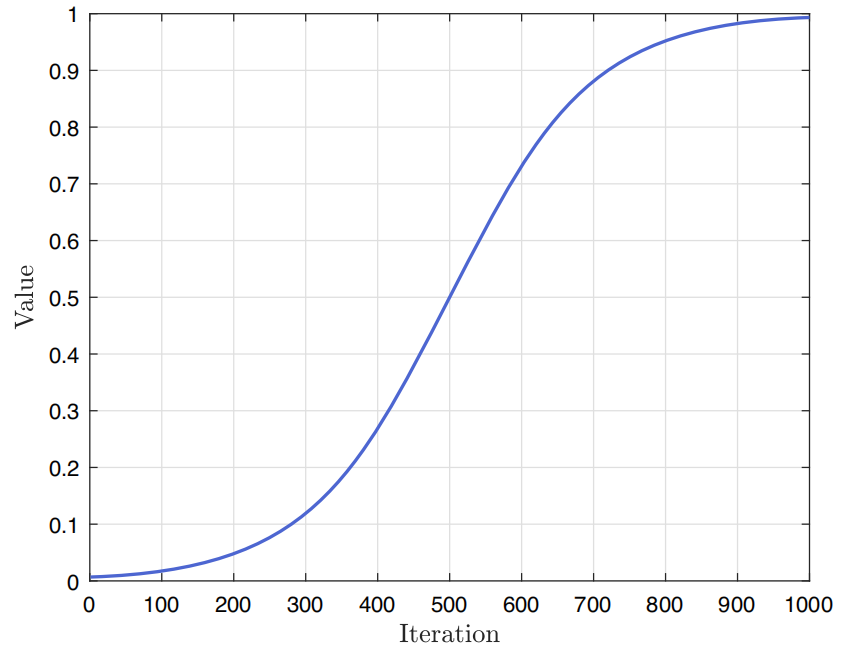
其中，参数隐式体现了吕佩尔狐的听觉能力，该能力随着迭代次数的增加而减弱，模拟狐狸在逐渐接近猎物时听觉敏感度的变化。该函数随迭代过程的变化如下图所示。

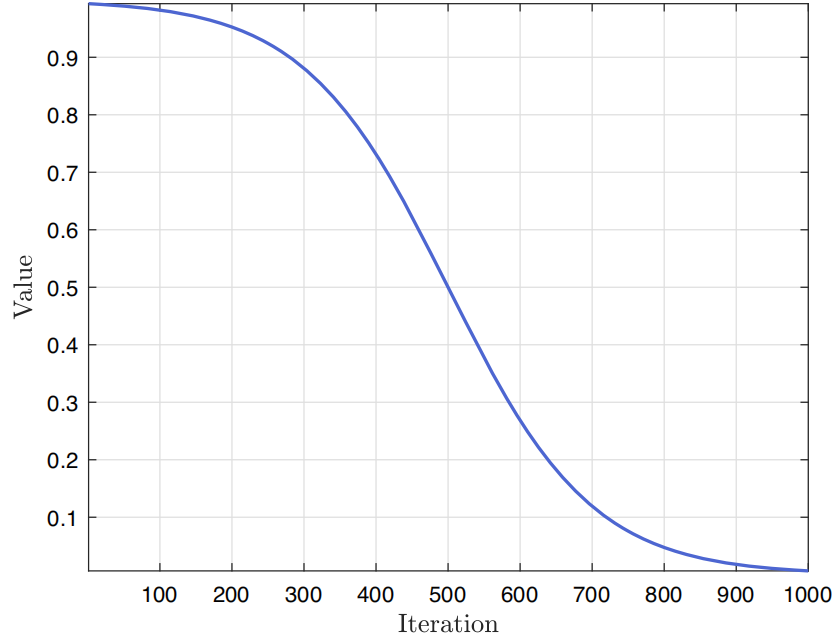
（3）旋转视角下的随机位置搜索

如前所述，吕佩尔狐凭借其眼睛的旋转特性，能够观察到周围超过260°的视野范围内的食物源。因此，可以通过计算模拟其基于旋转视角的搜索行为，使其根据猎物的位置调整自身位置。该行为可通过以下数学模型进行仿真：

其中，表示第只吕佩尔狐在第次迭代中，围绕全局最优位置旋转后的新位置；表示随机游走步长的限制，取值为；表示维度为的随机向量，其元素均匀分布于区间；是一个可在 0 和 1 之间切换的参数，其定义如下：

其中，rand 表示在区间内均匀分布的随机数，向量被定义为 1 或 -1，用以改变参数的取值。

其中，表示用于模拟吕佩尔狐视觉旋转特性的矩阵；而表示围绕视觉原点进行旋转的操作，其定义如下：

其中，表示二维平面内的旋转矩阵；符号表示新的位置经过平移，使得旋转中心位于原点

（4）听觉搜索

除了利用视觉的强度和旋转特性在白天定位猎物外，吕佩尔狐还会利用听觉进行猎物定位，但其对白天听觉的依赖程度低于视觉。同时，吕佩尔狐在白天的听觉灵敏度低于夜晚，因此白天更倾向于依赖视觉而非听觉。然而，在光照强烈的白昼，吕佩尔狐可能无法仅凭视觉和听觉定位猎物，此时它们会在搜索空间内随机漫游以寻找猎物。该行为可用以下公式进行模拟：

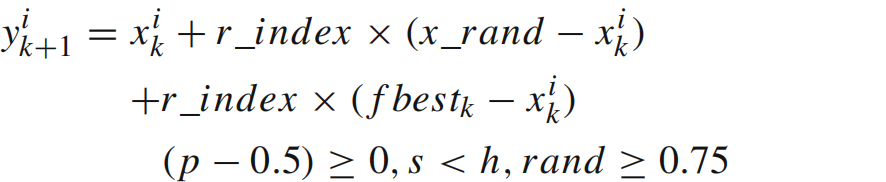
如前所述，吕佩尔狐可利用耳朵的旋转特性来定位猎物，其听觉范围覆盖以当前最优解为中心的150°圆形轨迹。此行为使吕佩尔狐能够从任意方向感知猎物的位置，且左右耳可分别、独立地捕捉声音信号。因此，吕佩尔狐会根据其耳朵“听到”的猎物位置更新自身位置。该行为可通过如下数学模型进行模拟：

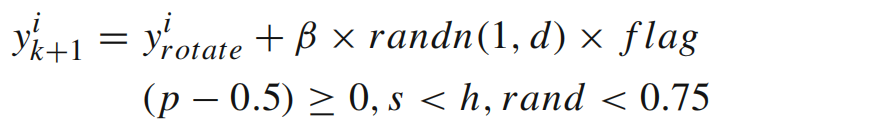
其中，分量的定义如下所示：

其中，参数表示吕佩尔狐为定位猎物所进行的耳部旋转角度，其定义如下所示：

下图展示了在二维搜索空间中，吕佩尔狐在白天通过视觉、听觉、视觉旋转特性以及双耳旋转特性更新其位置的方式。可以看出，最终位置将位于一个由吕佩尔狐当前所在位置所确定的圆形区域内的随机点。

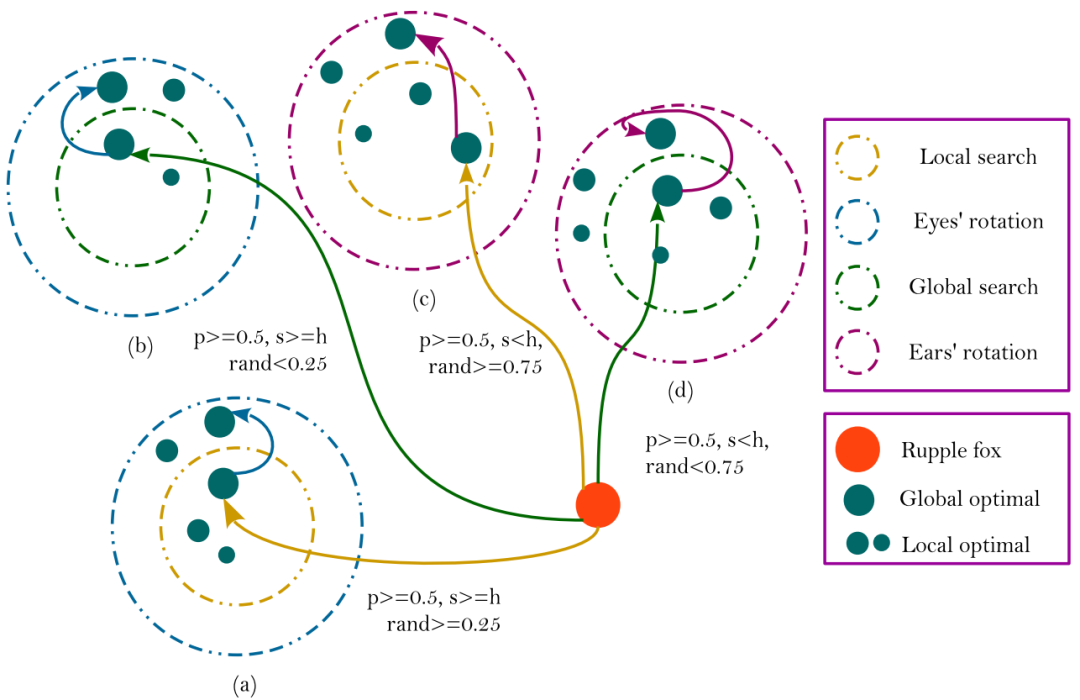
（5）夜间猎物搜索

在夜间，吕佩尔狐相较于视觉，更依赖其敏锐的听觉来发现猎物。此外，相比白天，它们在夜间的听觉灵敏度更强，因而能更有效地利用听觉获取猎物信息。然而，仅依赖上述两种夜间行为，吕佩尔狐仍可能无法准确找到猎物。在这种情况下，它们便会被迫在不同方向和位置随机觅食。该行为的建模过程如公式所示：

其中，表示当前模拟的吕佩尔狐行为模式发生在夜间，的定义如下：

其中，表示吕佩尔狐在多个候选位置中随机选择其最优位置，其具体定义如下所示：

在夜间，吕佩尔狐在寻找猎物时会同时利用听觉与视觉，但相比之下，它们更依赖于听觉。这是因为夜间视力较弱，而听觉灵敏度则相对更高，因此夜晚的听觉效果优于白天。吕佩尔狐被迫在搜索空间内的多个随机位置进行觅食。该行为可通过下式进行数学建模：

下图展示了吕佩尔狐在夜间如何在二维搜索空间中结合视觉、听觉、视觉旋转特性以及耳部旋转特性来更新自身位置。最终，其位置会落在搜索空间内以猎物位置为中心的某一随机圆域内。

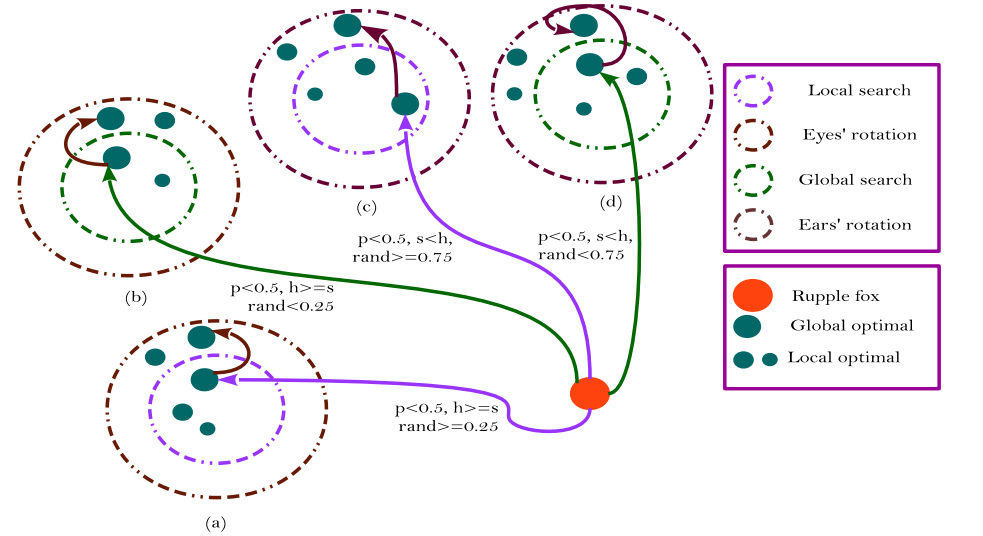
（6）利用嗅觉定位猎物

除了敏锐的听觉和视觉外，吕佩尔狐还具备出色的嗅觉能力，能够在昼夜间通过嗅觉搜索猎物，从而实现在搜索空间内的全域感知与探索。当吕佩尔狐逐渐接近猎物时，其嗅觉敏感度会呈指数级增强，直到精确定位到猎物的可能位置；相反，当其逐渐远离猎物时，嗅觉信号则呈指数衰减，直到意识到已偏离了猎物所在区域。在此类情况下，吕佩尔狐仍需在不同方向和区域内随机搜寻猎物。该行为可通过公式进行数学建模：

其中，、和表示取值范围在内的随机数。

参数作为时间的函数，该参数随迭代过程的变化曲线如下图所示，反映了吕佩尔狐的嗅觉特性如何随着猎物位置的变化而变化：在迭代初期至中期，嗅觉能力逐渐增强，达到搜索路径中心点附近的峰值；随后在迭代后半程逐渐减弱。

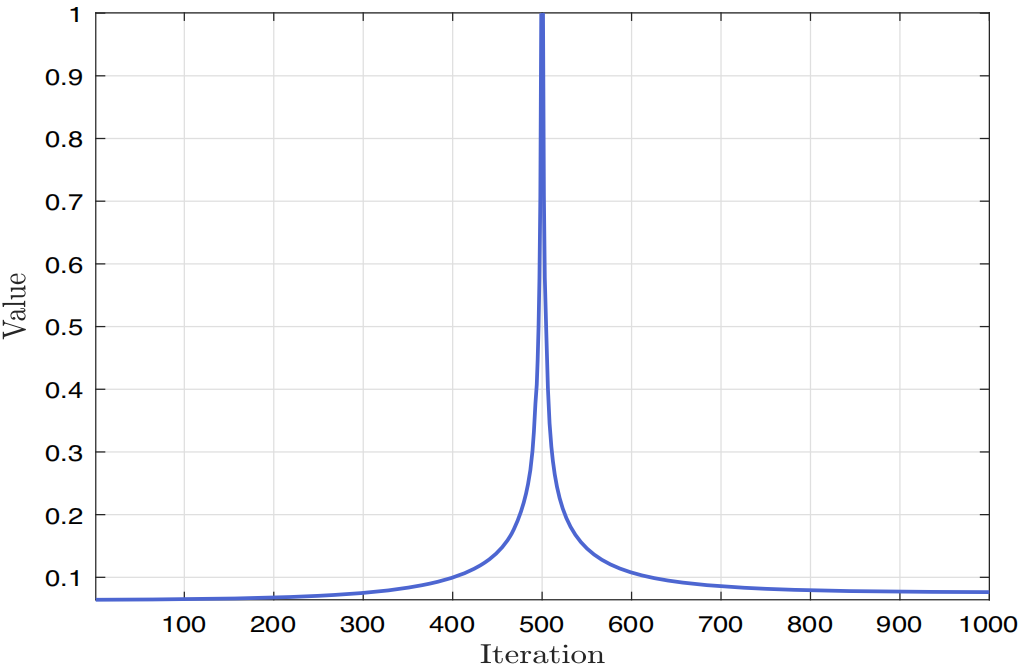
该参数被用于提升吕佩尔狐优化算法（RFO）的探索与开发能力，同时减缓搜索速度，强化收敛动态系统，从而使吕佩尔狐能够在更广泛的区域内觅食并充分利用每一搜索区域。通过这种机制，算法得以实现高效的收敛过程，并提升解决优化问题的性能。

下图展示了吕佩尔狐在二维搜索空间中，白天与夜间基于嗅觉更新位置的过程。显然，吕佩尔狐的最终位置位于以猎物为中心的某一随机圆域内。

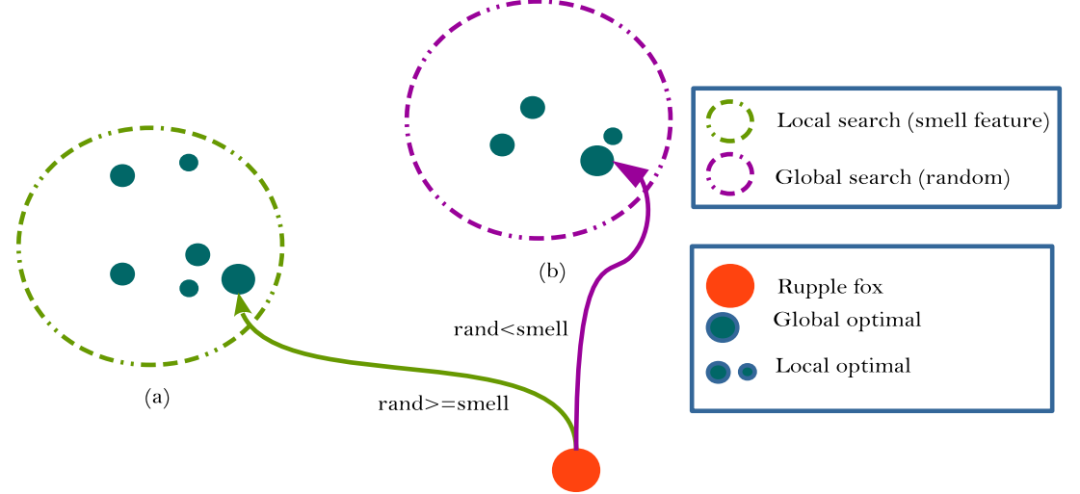
（7）向最佳吕佩尔狐位置移动

吕佩尔狐大部分时间都在寻找潜在猎物，猎物可能是最优的也可能是不利的，因此它们的位置不断变化。当它们听到、看到或嗅到猎物气味时，通常会朝向猎物移动。在此过程中，保留当前最优位置，并根据该最优位置更新其他吕佩尔狐的位置。在某些情况下，吕佩尔狐可能会直接移动到猎物位置，或者猎物会离开该区域继续觅食。此时，吕佩尔狐会继续在该区域内徘徊搜寻猎物，利用听觉和视觉进行追踪。

以下公式用于描述吕佩尔狐如何在向最佳候选解靠近的同时，进行随机猎物搜索的行为：

其中，和为正常数，均取值为 2；、和表示在区间内均匀分布的随机数；表示第只吕佩尔狐根据猎物位置更新后的坐标。

吕佩尔狐总是跟随靠近或非常接近最优猎物的最佳个体，如下图所示。该图展示了吕佩尔狐在二维搜索空间中，基于群体行为如何更新自身位置。显然，吕佩尔狐最终会停留在搜索空间内一个完全随机且被圆形区域包围的位置。

RFO优化算法的流程图如下所示：

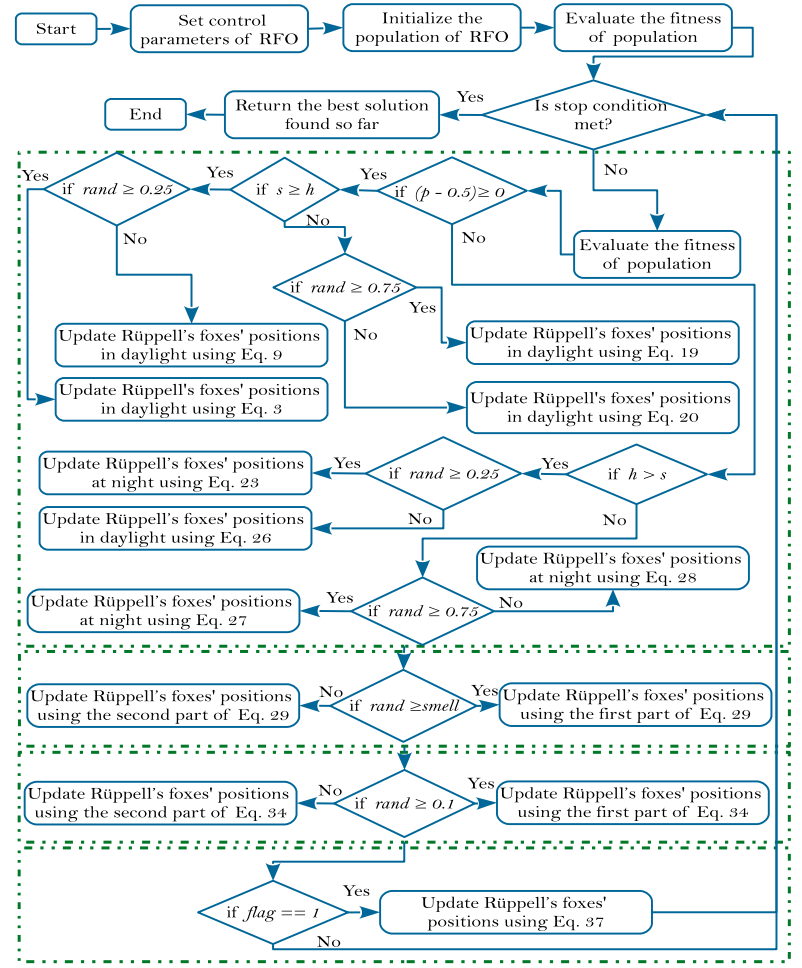
2 结果展示

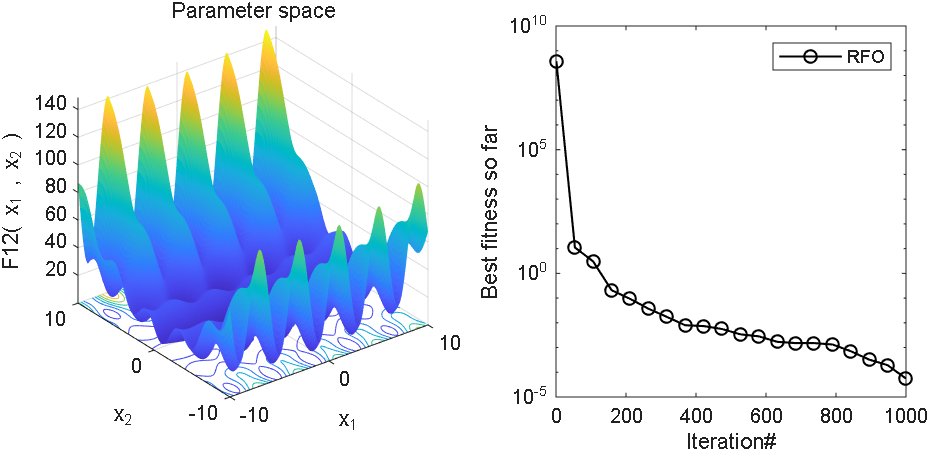
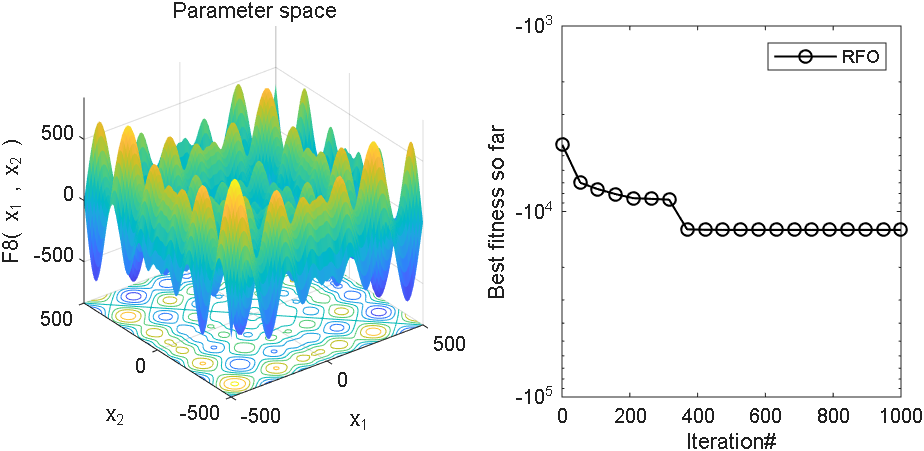
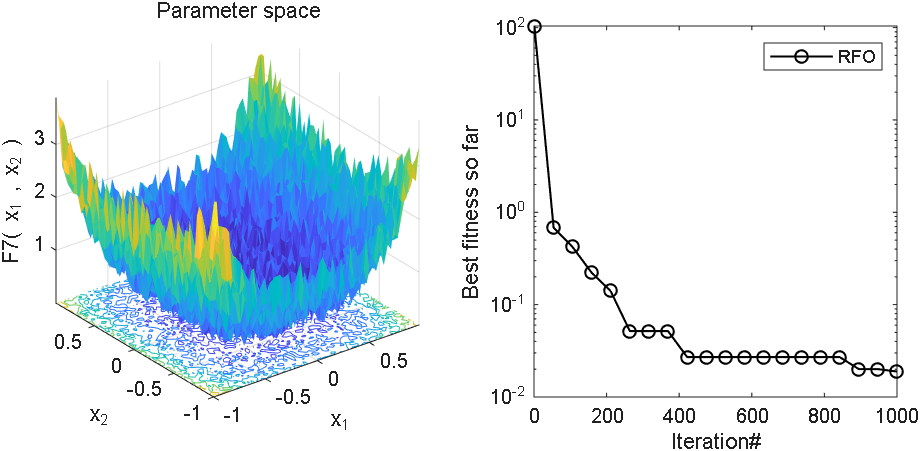
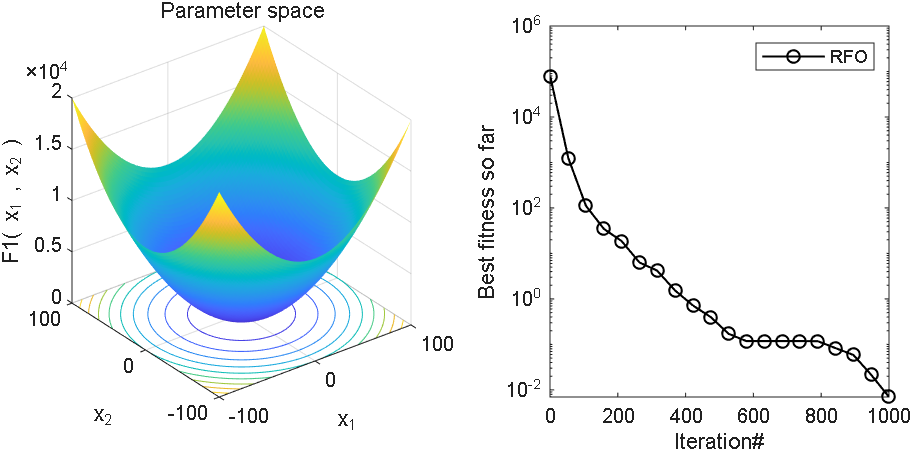
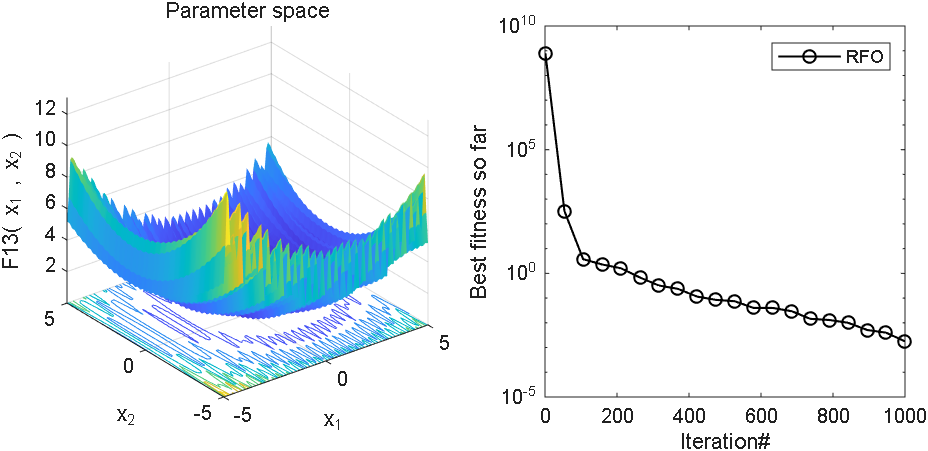
3、MATLAB核心代码

function [fmin0,fbest,ccurve]=RFO(rupplefoxes,itemax,lb,ub,dim,fobj)
%% Information
% % Rupple Fox Optimizer (RFO)
%  This code is designed for continuous, unconstrained, and single objective function minimization problems. 
% Input parameters
% rupplefoxes                       Population size
% itemax                   Maximum number of iterations
% lb                       Lower bound of a a particular problem
% ub                       Unuer bound of a particular problem
% dim:                     Number of decision variables
% fobj:                    Objective function to be minimized or maximized
% Output parameters
% fmin0                    Cost of global optimum solution
% fbest                    Global optimum solution
% ccurve                   Convergence curve obtained in solving an optimization problem
%% Convergence curve
ccurve=zeros(1,itemax);
% if size(ub,1)==1
%     ub=ones(dim,1)*ub;
%     lb=ones(dim,1)*lb;
% end

%{
f1 =  figure (1);
set(gcf,'color','w');
hold on
xlabel('Iteration','interpreter','latex','FontName','Times','fontsize',10)
ylabel('fitness value','interpreter','latex','FontName','Times','fontsize',10); 
grid;
%}

%% Start RFO 
% Initial population

fposition=initialization(rupplefoxes,dim,ub,lb); % Generation of initial solutions (position of rupple foxes)

%% Evaluate the initial fitness (fitness of the initial population)
fPos = zeros(rupplefoxes,dim);
fit = zeros(rupplefoxes,1);
for i=1:size(fposition,1)
     fit(i)=fobj(fposition(i,:));
end
 %% Initalize the parameters of RFO
fitness=fit; % Initial fitness of the random position of the rupple foxes

[fmin0,index]=min(fit);

pbest = fposition; % Initialization of the best positions
fbest = pbest(index,:); % initial global position
x=pbest;
L=100;
beta=1*10^-10;  %constant for walk rate update; this factor limits the step sizes of random walks
vec_flag=[1,-1];

%% Start RFO
for ite=1:itemax
 h=1/(1+exp((ite-itemax/2)/L)) ; % eyesight  decreasing (daylight) 1--0 up to night
 s=1/(1+exp((itemax/2 - ite)/L)) ; % % hear increasing (daylight) 0--1 (up to night)
 smell=(0.1/abs(acos((2/(1+exp((itemax/2 - ite)/100)))))); % up and down (variation)
%% Eyesight and hearing behaviors - at daylight and night
% Daylight
if (rand>=0.5) % daylight
        for i=1:size(fposition,1)
             ds=ceil(rupplefoxes*rand(1,rupplefoxes));
            if s>=h % % eyesight > hear  % based on eyes
              if rand>=0.25 %first phase (daylight sight is better) % exploration
                   X_randm = pbest(ds(i),:);
                   rand_index = floor(4*rand()+1)*rand;             
                  fposition(i,:)= 1*x(i,:) +rand_index*(X_randm - x(i,:))*1 +rand_index*(fbest-x(i,:))*1; % Exploitation
                  theta = (rand*260*2*pi/360);
                  fposition(i,:) = frotate(fposition(i,:),X_randm, theta, dim); % Exploration   
                 else % second phase
                    flag_index = floor(2*rand()+1);
                    Flag=vec_flag(flag_index);
                    X_randm = pbest(ds(i),:);
                     fposition(i,:)=X_randm+1*beta*randn(1,dim)*Flag;% The step factor limits the step sizes of random walks % Exploration   
                end
            else % hear > eysight  
                if (rand >=0.75) %daylight 
                  X_randm = pbest(ds(i),:);
                  rand_index = floor(4*rand()+1)*rand;%    

                  fposition(i,:)= 1*x(i,:) +rand_index*(X_randm - x(i,:))*1 +rand_index*(fbest-x(i,:))*1;
                 theta = (rand*150*pi/180);
                 fposition(i,:) = frotate(fposition(i,:),X_randm, theta, dim);  

                  else % second phase
                    flag_index = floor(2*rand()+1);
                    Flag=vec_flag(flag_index);
                    fposition(i,:)=pbest(ds(i),:)+1*beta*randn(1,dim)*Flag;% The beta factor limits the step sizes of random walks % Exploration   

                end
                
            end
            
        end
else
    % Night
    for i=1:size(fposition,1) % night
         dr=floor(rupplefoxes*rand(1,rupplefoxes))+1; 
            if h>=s %  
               if rand>=0.25 %first phase % exploration
                    X_randm = pbest(dr(i),:);
                  rand_index = floor(4*rand()+1)*rand;% 
                   
                  fposition(i,:)= 1*x(i,:) +rand_index*(X_randm - x(i,:))*1 +rand_index*(fbest-x(i,:))*1; % Expolitation
                 
                  theta =( rand*150*pi/360);
                  fposition(i,:) = frotate(fposition(i,:),X_randm, theta, dim); % Exploration    
                 
                else % second phase
                    
                 flag_index = floor(2*rand()+1);
                  Flag=vec_flag(flag_index);
                     
                    fposition(i,:)=pbest(dr(i),:)+1*beta*randn(1,dim)*Flag;% The beta factor limits the step sizes of random walks % Exploration   
                end
            else % hear < eysight 
                
                if (rand >=0.75) %daylight 
                   X_randm = pbest(dr(i),:);
                   rand_index = floor(4*rand()+1)*rand;% 

                 fposition(i,:)= 1*x(i,:) +rand_index*(X_randm - x(i,:))*1 +rand_index*(fbest-x(i,:))*1;
                 
                 theta = (rand*260*2*pi/180);
                 fposition(i,:) = frotate(fposition(i,:),X_randm, theta, dim);  
                  else % second phase
           
                      flag_index = floor(2*rand()+1);
            
                      Flag=vec_flag(flag_index);
            
                      fposition(i,:)=pbest(dr(i),:)+1*beta*randn(1,dim)*Flag;% The beta factor limits the step sizes of random walks % Exploration   

                end
                
            end
    end 
end

%% Smell behavior

for i=1:size(fposition,1)
    %Exploitation Phase (Food Exists)
     if rand>=smell
         
         ss=floor(1*rand(1,rupplefoxes))+1; 
        
         X_randm1 = pbest(ss(i),:); 

                 xmin=2; xmax=4;
                xr=xmin+rand()*(xmax-xmin);
                eps=abs((4*rand()) - (1*rand()+rand()))/xr; 
                
                fposition(i,:)= x(i,:) +1*(X_randm1-x(i,:))*eps + 1*eps*(fbest - x(i,:));
     else
         flag_index = floor(2*rand()+1);
            
            Flag=vec_flag(flag_index);
            ss=floor(1*rand(1,rupplefoxes))+1;
            fposition(i,:)=pbest(ss(i),:)+beta*randn(1,dim)*Flag;% The factor 0.001 limits the step sizes of random walks
          end     
end

%% Animal behavior
for i=1:size(fposition,1)
    if rand>=h  

         ab=floor(rupplefoxes*rand(1,rupplefoxes))+1; 
         fposition(i,:)=pbest(ab(i),:)+beta*randn(1,dim)*1;
         
    else
                ab=floor(rupplefoxes*rand(1,rupplefoxes))+1; 
                X_randp = pbest(ab(i),:); 
                 
              Dista=2*(fbest -fposition(i,:))*rand;
              Distb=3.0*(X_randp-pbest(i,:))*rand;
              flag_index = floor(2*rand()+1); 
              Flag=vec_flag(flag_index);
                 if(i==1)
                    fposition(i,:)=fposition(i,:)+1*Dista*1+Distb*Flag;
                else
                   fPos(i,:)= fposition(i,:)+1*Dista*1+Distb*Flag;
                   fposition(i,:)=(fPos(i,:)+fposition(i-1,:))/(2);
                 end
end
end

%% Worst Case Exploration
for i=1:size(fposition,1)
            flag_index = floor(2*rand()+1);
            fox=vec_flag(flag_index);
            if fox==1
                [~, gworst] = max(fitness);
                fposition(gworst,:)=fposition(gworst,:) + beta*randn(1,dim);  
            end
end
%%  Handling boundary violations
for i=1:size(fposition,1)
     if fposition(i,:)<lb
        fposition(i,:)=lb;
     elseif fposition(i,:)>ub
            fposition(i,:)=ub;
     end
 end
%% Update global, best and new position
    for i=1:size(fposition,1) 

         if fposition(i,:)>=lb & fposition(i,:)<=ub 

         x(i,:)=fposition(i,:); 

          ub_=fposition(i,:)>ub;
          lb_=fposition(i,:)<lb;
         
        fposition(i,:)=(fposition(i,:).*(~(ub_+lb_)))+ub.*ub_+lb.*lb_;
        
          fit(i)=fobj(fposition(i,:)); % calculate the objective function

  % Update if the solution improves 
            if (fit(i)<fitness(i)) 
                 pbest(i,:) = fposition(i,:); % Update the best fposition 
                 fitness(i)=fit(i); % Update the fitness

            end
  % % Updating fbest and best fitness
          
            if (fitness(i)<fmin0)
               fmin0=fitness(i);
               fbest = pbest(i,:); % Update the global best positions
            end 
        end
    end

  outmsg = ['Iteration# ', num2str(ite) , '  Fitness= ' , num2str(fmin0)];
  disp(outmsg);

   ccurve(ite)=fmin0; % Best found value until iteration ite

   %{
if ite>2
     set(0, 'CurrentFigure', f1)

        line([ite-1 ite], [ccurve(ite-1) ccurve(ite)],'Color','b'); 
        title({'Convergence characteristic curve'},'interpreter','latex','FontName','Times','fontsize',12);
        xlabel('Iteration');
        ylabel('Best score obtained so far');
        drawnow 
 end 
   %}
 end

end

参考文献

[1] Braik M, Al-Hiary H. Rüppell’s fox optimizer: A novel meta-heuristic approach for solving global optimization problems[J]. Cluster Computing, 2025, 28(5): 1-77.

完整代码获取

后台回复关键词：

TGDM876

获取更多代码：

或者复制链接跳转：https://docs.qq.com/sheet/DU3NjYkF5TWdFUnpu