成功历史智能优化器，原理详解，MATLAB代码免费获取

成功历史智能优化器（Success history intelligent optimizer，SHIO）是一种新的随机群智能算法，它提供了一种解决单目标优化问题的方法，提出了一种新的探索和开发运动策略，该策略基于在搜索空间中找到的三个最佳解来创建一个新的运动向量，其中每个最佳解存储在内存中，并从优化过程中迄今为止找到的三个最佳解的平均值中减去。所提出的SHIO保证了搜索空间探索和使用的效率。

该算法能够探索不同的搜索区域位置，在优化的同时充分利用潜在的搜索空间位置，避免局部乐观，有效地收敛到全局最优。SHIO提供了高度竞争力和上级的结果，在评估的单峰和多峰的基准比较算法。该成果于2022年发表在知名SCI期刊The Journal of Supercomputing上。

SHIO算法分为以下三个阶段：1.初始化阶段：在这个阶段中，随机定义和初始化问题的解的初始值—算法参数。然后，这些最初猜测的解决方案将通过在第二阶段中提出的运动方程迭代改进。2.迭代阶段：在这个阶段，解决方案将通过算法提供的方程迭代改进，直到满足停止标准。3.寻找最佳解决方案阶段：在此阶段，通过补偿目标函数中的值并比较结果来提供算法的最佳解。这三个阶段在算法伪代码的SHIO步骤中详细介绍，如下图所示。

1、算法原理

（1）种群初始化

该阶段是优化算法的核心。迭代阶段的目标是根据以下运动方程找到全局最佳值。

在初始阶段生成所需的种群后，迭代阶段开始。

其中Δ1i、Δ2i定义第i个粒子的最优位置和次优位置，Ci是第一个当前粒子位置，Mi是第i个粒子的平均点位置，A表示粒子搜索的区域。注意，在[0，1]中有r个随机数。它为方程提供随机行为，||表示绝对值。Mi表示移动方向，可以在解决方案和目的地之间的空间中，也可以在解决方案和目的地之外。A定义了移动应该朝向或向外移动目标区域的距离。r为目的地带来随机权重，以便在定义距离时随机强调目的地的影响。当前位置（Ci）是加到平均点位置的向量。给定三个向量，平均位置向量（Mi）和当前粒子位置（Ci），我们形成它们的和。我们平移当前粒子位置的向量，直到它的尾部与（Mi）的头部重合。然后，从（Mi）的尾部到当前粒子位置的头部的有向线段是加法的向量。

（2）基于历史的适应战略

在上述公式的基础上，进一步引入运动方程，SHIO保持着三个粒子Δ1和Δ2的历史记忆。在每次迭代中，粒子使用最佳解Δ1、Δ2和Δ3来确定下一个位置以及它应该如何在搜索空间中移动。

其中Δ3i定义第i个粒子的在第三佳解位置。

Δ1、Δ2和Δ3值由成功的个体使用，并且在生成结束时，存储器的内容被更新如下：

其中，存储器IMR1、IMR2和IMR3存储着每代的第一最佳解Δ1、第二最佳解Δ2和第三佳解Δ3的值，index[k]（1 ≤ k ≤ H）决定了内存中要更新的位置。在搜索开始时，k被初始化为1。每当有新元素插入到历史中时，k递增。在迭代G中，更新存储器中的第k个元素。在更新过程中，迭代I中的所有个体的值都小于gbest1和gbest2。

此外，加权平均值Mi使用下式更新，Mi用于影响粒子运动。

使用SHIO，每个个体都是搜索空间中的一个点（或粒子），代表所研究的优化问题的候选解。该算法通过控制各个候选解的移动来驱动最优解。与传统的PSO算法不同，SHIO算法中的三个最佳解控制着整个群体的运动，即Δ1，Δ2和Δ3。

（3）寻找最佳解决方案阶段

SHIO算法中，建议将矢量步长值选择为域的一部分（对于多维搜索空间的每个维度），如下式所示

其中Xmax和Xmin分别是x和5的域的最大值和最小值。SHIO算法使用SV而不是Vmax。SV在更新过程中负责平衡勘探和开采的矛盾目标。 用于控制SV的方程式如下所述。SV的值从1.5线性减小到0

2、结果展示

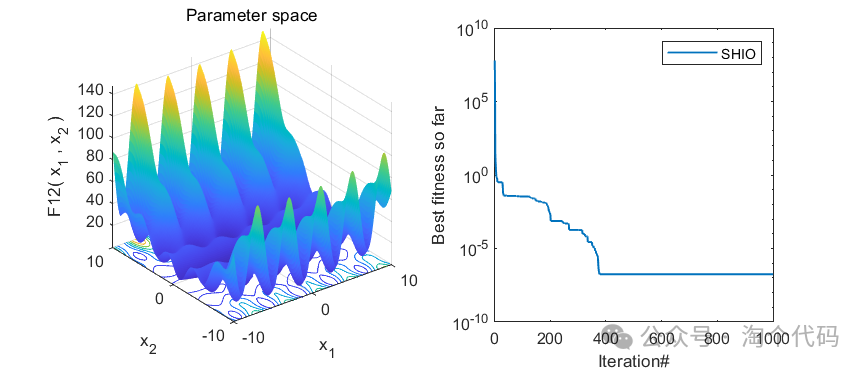
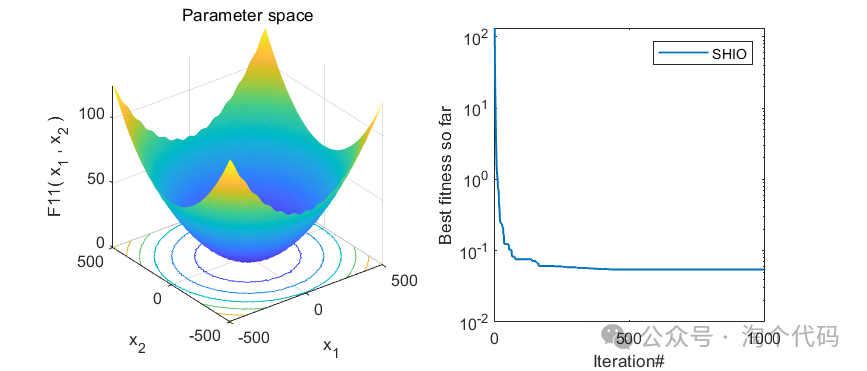
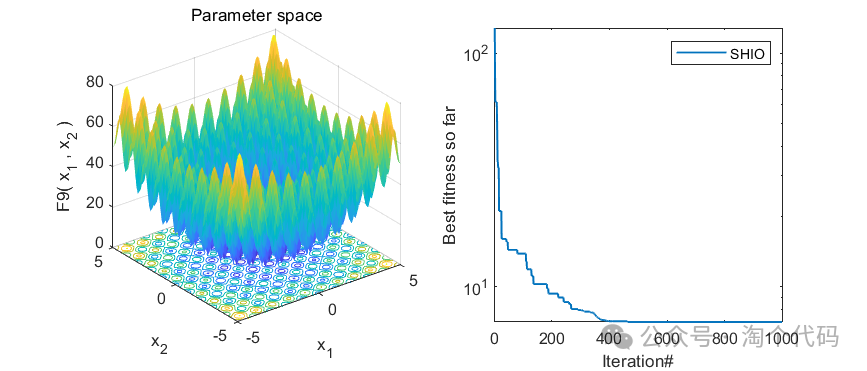
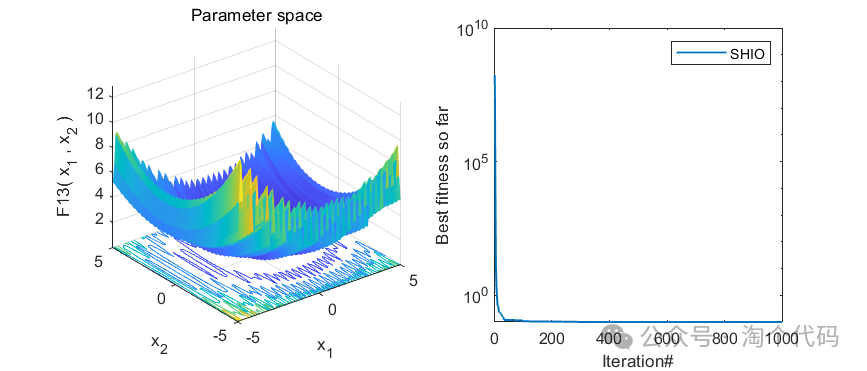
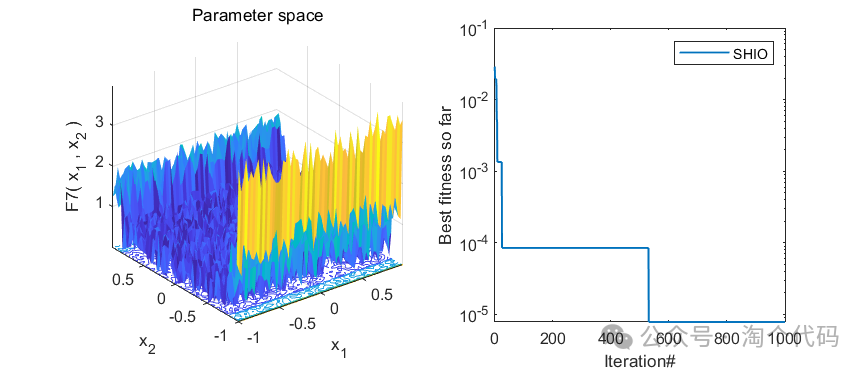
3、MATLAB核心代码

function [bstVal, fstPos, convCurve, traj, fitHist, posHist] = SHIOoptmizer(pNum, maxIter, lb, ub, dim, costFunc)
% Initialize solutions
fstPos = zeros(1, dim);
fstVal = inf;
sndPos = zeros(1, dim);
sndVal = inf;
thrdPos = zeros(1, dim);
thrdVal = inf;
bstVal = inf;
alpha = 1.5;

deltaPos1 = zeros(1, maxIter);
fit1 = zeros(1, pNum);
fitHist = zeros(pNum, maxIter);
posHist = zeros(pNum, maxIter, dim);
traj = zeros(pNum, maxIter);

% Initialize particle positions
meanPos = initialization(pNum, dim, ub, lb);
convCurve = zeros(1, maxIter);
iter = 0;

% Main loop
while iter < maxIter
    iter = iter + 1;
    for i = 1:size(meanPos, 1)
        % Handle boundary conditions
        ubFlag = meanPos(i,:) > ub;
        lbFlag = meanPos(i,:) < lb;
        meanPos(i,:) = meanPos(i,:) .* ~(ubFlag + lbFlag) + ub .* ubFlag + lb .* lbFlag;
        
        % Evaluate fitness
        fit = costFunc(meanPos(i,:));
        updateSolutionHierarchy(fit, meanPos(i,:));
        
        % Store fitness and positions
        fit1(i) = fit;
        fitHist(i, iter) = fit;
        posHist(i, iter, :) = meanPos(i,:);
        traj(:, iter) = meanPos(:, 1);
    end
    
    % Update positions
    alpha = alpha - 0.004;
    for i = 1:pNum
        for j = 1:dim
            X1 = updatePosition(fstPos(j), meanPos(i,j), alpha);
            X2 = updatePosition(sndPos(j), meanPos(i,j), alpha);
            X3 = updatePosition(thrdPos(j), meanPos(i,j), alpha);
            meanPos(i,j) = (X1 + X2 + X3) / 3;
        end
    end
    updateBestValue();
    convCurve(iter) = bstVal;
end

    function updateSolutionHierarchy(fitness, position)
        if fitness < fstVal
            [thrdVal, sndVal, fstVal] = deal(sndVal, fstVal, fitness);
            [thrdPos, sndPos, fstPos] = deal(sndPos, fstPos, position);
        elseif fitness < sndVal
            [thrdVal, sndVal] = deal(sndVal, fitness);
            [thrdPos, sndPos] = deal(sndPos, position);
        elseif fitness < thrdVal
            thrdVal = fitness;
            thrdPos = position;
        end
    end

    function X = updatePosition(best, current, a)
        X = best + (a * 2 * rand() - a) * abs(rand() * best - current);
    end

    function updateBestValue()
        bstVal = min([bstVal, fstVal, sndVal, thrdVal]);
    end
end

参考文献

[1]Fakhouri H N, Hamad F, Alawamrah A. Success history intelligent optimizer[J]. The Journal of Supercomputing, 2022, 78(5): 6461-6502.

完整代码获取

后台回复关键词：

TGDM900

点击下方卡片关注，获取更多代码