Cesium加载3Dtiles模型的平移和旋转

原创 已于 2024-03-27 13:59:26 修改 · 4.2k 阅读 · 29 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法

于 2024-03-27 13:56:43 首次发布
该篇文章介绍了如何在Cesium中操作3Dtiles模型，涉及平移和旋转的数学原理及其实现步骤，适合GIS开发者和Cesium用户阅读。

Cesium加载3Dtiles模型的平移和旋转

一、基础说明

  • Cesium中点由Cartesian3 表示，类似POINT3D点，其形式为包含 (x, y, z)的一维向量

  • Cesium中默认坐标系以地心为原点，所有未指明的Cartesian3 都基于此坐标系

  • 我们需要进行的平移与旋转基于模型所在点为原点，正东为X，正北为Y的局部坐标系

  • 使用函数Cesium.Transforms.eastNorthUpToFixedFrame(origin) 获取上述局部坐标系中点转换为世界坐标系中的位置的变换矩阵，P世界=M变换矩阵P局部

  • 3Dtiles模型的变换由一个4维矩阵完成，通过不断左乘变换矩阵可以完成一系列的复杂变换

二、模型平移与调整透明度

使用vue2，参考官方调整模型高度的案例。

  1. 假设模型的原点在世界坐标系下坐标为(xorigin, yorigin, zorigin)

  2. 获取坐标系变换矩阵

  3. 假设模型需要平移(x, y, z)量，先计算局部坐标系中点(x, y, z)在世界坐标下的位置(xworld, yworld, zworld)

    const offset = Cesium.Matrix4.multiplyByPoint(m, tempTranslation, new Cesium.Cartesian3(0, 0, 0));

  4. 使用(xworld, yworld, zworld)-(xorigin, yorigin, zorigin)获得世界坐标系中平移向量

  5. 使用Cesium.Matrix4.fromTranslation(translation); 获取3Dtiles平移变换矩阵

  6. 透明度调整tileset.style = new Cesium.Cesium3DTileStyle({color: "color('rgba(255,255,255," + opacity + ")')"});

transferModel(tileset, _tx, _ty, _tz,_opacity) {
      if(!this.checkModelLoad()){
        return
      }
      let tx = _tx ? _tx : 0;
      let ty = _ty ? _ty : 0;
      let tz = _tz ? _tz : 0;
      let opacity = _opacity ? _opacity/100 : 1

      const origin = tileset.boundingSphere.center;

      const m = Cesium.Transforms.eastNorthUpToFixedFrame(origin);//获取到以模型中心为原点,Z轴垂直地表的局部坐标系，以矩阵表示，此矩阵为将局部坐标系变换到世界坐标系的变换矩阵
      //平移
      const tempTranslation = new Cesium.Cartesian3(tx, ty, tz);//平移向量
      const offset = Cesium.Matrix4.multiplyByPoint(m, tempTranslation, new Cesium.Cartesian3(0, 0, 0));//局部坐标中（tx,ty,tz)在世界坐标系中位置
      const translation = Cesium.Cartesian3.subtract(offset, origin, new Cesium.Cartesian3());//终点世界坐标减去原点世界坐标得到世界坐标系下平移向量
      tileset.modelMatrix = Cesium.Matrix4.fromTranslation(translation);
      //透明度
      tileset.style = new Cesium.Cesium3DTileStyle({
        color: "color('rgba(255,255,255," + opacity + ")')",
      });
    },

三、模型旋转

模型旋转时，由于Cesium默认绕轴旋转是绕世界坐标系轴旋转，因此我们需要做如下操作完成绕局部坐标轴旋转

  1. 将模型原点平移回世界坐标系原点（地心），矩阵记为T1

  2. 将局部坐标Z轴调整到与世界坐标Z轴重合，矩阵记为R1

  3. 将模型绕世界坐标系的某个轴旋转（真正进行旋转的矩阵），此处以Z轴为例，矩阵记为R

  4. 将局部坐标Z轴旋转回原来的指向，矩阵记为R2

  5. 平移回初始位置，矩阵记为T2

最终模型旋转的矩阵为T2R2RR1T1

将旋转开始前模型的初始变换矩阵左乘此矩阵即可完成旋转变换

（一）回到地心

	  const origin = tileset.boundingSphere.center;
      console.log("初始世界坐标", origin)
      const localToWorldMatrix = Cesium.Transforms.eastNorthUpToFixedFrame(origin);//获取到以模型中心为原点,Z轴垂直地表的局部坐标系的变换矩阵，左乘此矩阵可以将局部坐标变换为世界坐标
      const originMatrix = tileset.modelMatrix//贴地变换矩阵或者初始变换矩阵M0
      console.log("当前坐标变换矩阵", localToWorldMatrix)
      const backToEarthCenter = new Cesium.Cartesian3(-origin.x, -origin.y, -origin.z)//回到地心位移量
      let backToEarthCenterMatrix = Cesium.Matrix4.fromTranslation(backToEarthCenter);//回到地心变换矩阵
      Cesium.Matrix4.multiply(backToEarthCenterMatrix, originMatrix, backToEarthCenterMatrix)//贴地变换矩阵左乘回到地心矩阵 T1M0
      console.log("回到地心变换矩阵", backToEarthCenterMatrix)

（二）局部Z轴校正

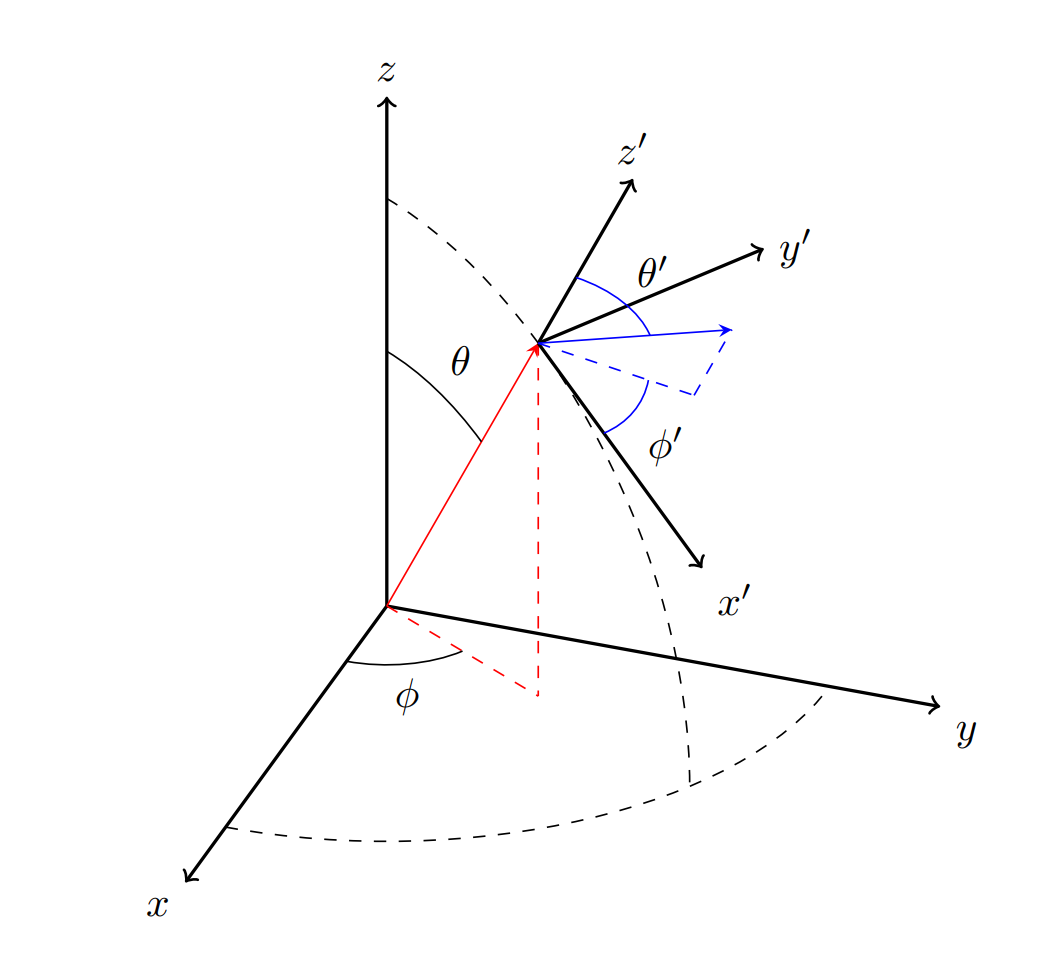
坐标轴校正示意图

先将红线表示的向量（z'轴）绕Z轴顺时针旋转Φ度，再绕Y轴顺时针旋转θ度

1、通过一维向量表示坐标轴，通过左乘变换矩阵完成局部坐标轴在世界坐标系下的表示

//旋转模型使得Z轴与世界坐标Z轴重合
      let arrowX = new Cesium.Cartesian3(1, 0, 0)
      let arrowY = new Cesium.Cartesian3(0, 1, 0)
      let arrowZ = new Cesium.Cartesian3(0, 0, 1)
      let localArrowX = Cesium.Matrix4.multiplyByPoint(localToWorldMatrix, new Cesium.Cartesian3(1, 0, 0), new Cesium.Cartesian3)
      let localArrowY = Cesium.Matrix4.multiplyByPoint(localToWorldMatrix, new Cesium.Cartesian3(0, 1, 0), new Cesium.Cartesian3)
      let localArrowZ = Cesium.Matrix4.multiplyByPoint(localToWorldMatrix, new Cesium.Cartesian3(0, 0, 1), new Cesium.Cartesian3)

2、先绕世界Z轴旋转局部Z轴到世界XOZ面上，再旋转到Z轴上

  • Cesium.Cartesian3.angleBetween 可计算两个向量间的弧度

  • Cesium.Cartesian3.angleBetween(arrowX, new Cesium.Cartesian3(localArrowZ.x, localArrowZ.y, 0)) 即为Φ对应弧度

  • Cesium.Cartesian3.angleBetween(localArrowX, arrowZ)即为θ对应弧度

  • Cesium.Matrix3.fromRotationX、Cesium.Matrix3.fromRotationY、Cesium.Matrix3.fromRotationZ 的旋转正方向为逆时针，传入参数为弧度

3、需要注意由于只对齐了Z轴，如需绕X轴，Y轴旋转需要做类似的处理

let angleToXZ = Cesium.Cartesian3.angleBetween(arrowX, new Cesium.Cartesian3(localArrowZ.x, localArrowZ.y, 0))//局部Z轴在世界坐标系XY平面上投影到X轴角度，即绕Z顺时针旋转这个角度可以到XZ平面上
      let angleToZ = Cesium.Cartesian3.angleBetween(localArrowX, arrowZ)//然后绕Y轴顺时针旋转此角度可使得Z轴与世界坐标系Z轴重合
      const rotationAngleToXZ = Cesium.Matrix3.fromRotationZ(-angleToXZ);//此函数正方向为逆时针
      const rotationAngleToZ = Cesium.Matrix3.fromRotationY(-angleToZ);
      let rotationAngleToZMatrix = Cesium.Matrix3.multiply(rotationAngleToZ, rotationAngleToXZ, new Cesium.Matrix3)
      rotationAngleToZMatrix = Cesium.Matrix4.fromRotationTranslation(rotationAngleToZMatrix)
      Cesium.Matrix4.multiply(rotationAngleToZMatrix, backToEarthCenterMatrix, rotationAngleToZMatrix)//局部轴校正R1T1M0

（三）真实旋转矩阵

此处完成真正需要进行的旋转，此处以绕Z轴旋转为例

      // 绕Z轴旋转
      console.log(rz - this.originRz)
      const rotationZ = Cesium.Matrix3.fromRotationZ(Cesium.Math.toRadians(rz - this.originRz)); // 绕Z轴旋转变换矩阵R
      let rotationMatrix = Cesium.Matrix4.fromRotationTranslation(rotationZ)
      Cesium.Matrix4.multiply(rotationMatrix, rotationAngleToZMatrix, rotationMatrix)//RR1T1M0

（四）局部Z轴回位

将局部Z轴回到原本的指向，即刚刚旋转的角度取负值，此处需要注意变换的顺序，后进行的变换先复位

  • 校正矩阵：Cesium.Matrix3.multiply(rotationAngleToZ, rotationAngleToXZ, new Cesium.Matrix3)

  • 复位矩阵：Cesium.Matrix3.multiply(rotationAngleLeaveXZ, rotationAngleLeaveZ, new Cesium.Matrix3)

      // 旋转模型回到原本朝向
      const rotationAngleLeaveXZ = Cesium.Matrix3.fromRotationZ(angleToXZ);
      const rotationAngleLeaveZ = Cesium.Matrix3.fromRotationY(angleToZ);
      let rotationAngleLeaveZMatrix = Cesium.Matrix3.multiply(rotationAngleLeaveXZ, rotationAngleLeaveZ, new Cesium.Matrix3)
      rotationAngleLeaveZMatrix = Cesium.Matrix4.fromRotationTranslation(rotationAngleLeaveZMatrix)// 局部Z轴回到原本方向
      Cesium.Matrix4.multiply(rotationAngleLeaveZMatrix, rotationMatrix, rotationAngleLeaveZMatrix)//R2RR1T1M0

（五）回到原本位置

位移量即为模型原本的世界坐标，直接可获得变换矩阵

      //回到原来位置
      const backToOriginMatrix = Cesium.Matrix4.fromTranslation(origin);//从地心回归原位T2

（六）绕Z轴旋转完整代码

rotationModel(tileset,rz) {

      if(!this.checkModelLoad()){
        return
      }
      const origin = tileset.boundingSphere.center;
      console.log("初始世界坐标", origin)
      const localToWorldMatrix = Cesium.Transforms.eastNorthUpToFixedFrame(origin);//获取到以模型中心为原点,Z轴垂直地表的局部坐标系的变换矩阵，左乘此矩阵可以将局部坐标变换为世界坐标
      const originMatrix = tileset.modelMatrix//贴地变换矩阵或者初始变换矩阵M0
      console.log("当前坐标变换矩阵", localToWorldMatrix)
      const backToEarthCenter = new Cesium.Cartesian3(-origin.x, -origin.y, -origin.z)//回到地心位移量
      let backToEarthCenterMatrix = Cesium.Matrix4.fromTranslation(backToEarthCenter);//回到地心变换矩阵
      Cesium.Matrix4.multiply(backToEarthCenterMatrix, originMatrix, backToEarthCenterMatrix)//贴地变换矩阵左乘回到地心矩阵 T1M0
      console.log("回到地心变换矩阵", backToEarthCenterMatrix)
      // 旋转
      //旋转模型使得Z轴与世界坐标Z轴重合
      let arrowX = new Cesium.Cartesian3(1, 0, 0)
      let arrowY = new Cesium.Cartesian3(0, 1, 0)
      let arrowZ = new Cesium.Cartesian3(0, 0, 1)
      let localArrowX = Cesium.Matrix4.multiplyByPoint(localToWorldMatrix, new Cesium.Cartesian3(1, 0, 0), new Cesium.Cartesian3)
      let localArrowY = Cesium.Matrix4.multiplyByPoint(localToWorldMatrix, new Cesium.Cartesian3(0, 1, 0), new Cesium.Cartesian3)
      let localArrowZ = Cesium.Matrix4.multiplyByPoint(localToWorldMatrix, new Cesium.Cartesian3(0, 0, 1), new Cesium.Cartesian3)
      let angleToXZ = Cesium.Cartesian3.angleBetween(arrowX, new Cesium.Cartesian3(localArrowZ.x, localArrowZ.y, 0))//局部Z轴在世界坐标系XY平面上投影到X轴角度，即绕Z顺时针旋转这个角度可以到XZ平面上
      let angleToZ = Cesium.Cartesian3.angleBetween(localArrowX, arrowZ)//然后绕Y轴顺时针旋转此角度可使得Z轴与世界坐标系Z轴重合
      const rotationAngleToXZ = Cesium.Matrix3.fromRotationZ(-angleToXZ);//此函数正方向为逆时针
      const rotationAngleToZ = Cesium.Matrix3.fromRotationY(-angleToZ);
      let rotationAngleToZMatrix = Cesium.Matrix3.multiply(rotationAngleToZ, rotationAngleToXZ, new Cesium.Matrix3)
      rotationAngleToZMatrix = Cesium.Matrix4.fromRotationTranslation(rotationAngleToZMatrix)
      Cesium.Matrix4.multiply(rotationAngleToZMatrix, backToEarthCenterMatrix, rotationAngleToZMatrix)//局部轴校正R1T1M0


      // 绕Z轴旋转
      console.log(rz - this.originRz)
      const rotationZ = Cesium.Matrix3.fromRotationZ(Cesium.Math.toRadians(rz - this.originRz)); // 绕Z轴旋转变换矩阵R
      let rotationMatrix = Cesium.Matrix4.fromRotationTranslation(rotationZ)
      Cesium.Matrix4.multiply(rotationMatrix, rotationAngleToZMatrix, rotationMatrix)//RR1T1M0

      // 旋转模型回到原本朝向
      const rotationAngleLeaveXZ = Cesium.Matrix3.fromRotationZ(angleToXZ);
      const rotationAngleLeaveZ = Cesium.Matrix3.fromRotationY(angleToZ);
      let rotationAngleLeaveZMatrix = Cesium.Matrix3.multiply(rotationAngleLeaveXZ, rotationAngleLeaveZ, new Cesium.Matrix3)
      rotationAngleLeaveZMatrix = Cesium.Matrix4.fromRotationTranslation(rotationAngleLeaveZMatrix)// 局部Z轴回到原本方向
      Cesium.Matrix4.multiply(rotationAngleLeaveZMatrix, rotationMatrix, rotationAngleLeaveZMatrix)//R2RR1T1M0

      //回到原来位置
      const backToOriginMatrix = Cesium.Matrix4.fromTranslation(origin);//从地心回归原位T2
      // 应用变换矩阵

      const lastMatrix = Cesium.Matrix4.multiply(backToOriginMatrix, rotationAngleLeaveZMatrix, new Cesium.Matrix4)//最终矩阵T2R2RR1T1M0

      tileset.modelMatrix = lastMatrix
      console.log("结束世界坐标", tileset.boundingSphere.center)
      this.originRz = rz

    },

white_mo
关注
第7节：cesium 3dtiles模型展示优化，平移、旋转、缩放...（含源码+视频）
qq_29384639的博客
06-04 3345
上一节，我们说明了如何加载3DTiles模型，这节我们主要说一下模型加载进来如何进行模型的展示优化。
Cesium 实战 21 - 三种方式（CZML、nodeTransformations）修改模型节点组件属性（比例、旋转、移动等）
非科班Java出身GISer的博客
08-08 2709
Cesium 实战教程 - 三种方式（CZML、nodeTransformations）修改模型节点组件属性（修改比例、旋转、移动等），实现模型动作、动画。
Cesium实战功能教程之3dtiles操作（移动+旋转）
coderzyq的博客
07-27 1166
在平常的工作中，难免会用到倾斜摄影，当加载倾斜摄影的时候，最头疼的就是倾斜摄影的偏移问题，在代码中进行修改加载倾斜摄影的偏移参数，虽然简单但过于麻烦，也耽误开发的效率，因此我就本着能不能在三维场景中对倾斜摄影进行手动操作，无需再改代码并可将倾斜摄影放在较为正确的位置。为了实现这个功能，我就从网上找一些相关的资料，参照一些网上的大佬的代码进行修改，并补充相关知识，并不是那么及时的完成了这篇文章。
3D Tiles 格式详解
最新发布
罗朝辉（飘飘白云）
10-21 1373
3D Tiles 技术指南摘要 3D Tiles 是 Cesium 开发的开放标准，用于高效流式传输和渲染大规模 3D 地理空间数据。本文档详细解析了 3D Tiles 的核心技术规范，包括： 层次化瓦片结构：通过树形组织和 LOD 机制实现渐进式加载 关键文件格式：tileset.json 定义数据集元信息，tile.json 描述瓦片属性 空间索引机制：支持 region/box/sphere 三种边界体积类型 渲染优化：基于几何误差的 LOD 选择和视锥剔除 实际应用：以德国法兰克福数据集为例展示文件
Cesium的一些坐标变换公式记录
qq_31121227的博客
06-06 3490
var daTAs = { code: '', longitude: 121.42875949287559, latitude: 31.198376344961723, height: 6, heading: 90, scale: 1, range: 50, bimshow: true, iseidting: false, ...
Cesium教程04_旋转模型
w131552的博客
11-24 1027
cesium旋转模型
详解Cesium3DTileset的平移、旋转、缩放(含封装好的代码)
weixin_70945905的博客
09-22 3409
每个函数都可以单独使用，代码去掉TS类型注释就可以在JS中使用了。
cesium 模型实体平移
ltsg_的博客
01-24 3723
先上最终实现图 关键点： 1.首先是箭头线图形，entity 实体中polyline 有一个PolylineArrowMaterialProperty字段可以生成箭头，具体实现官网上有，这里不做阐述 2.其次三个方向的坐标系的建立，单方向的轴，像点位置可以作为一个Z轴，然后去该轴和竖直方向的轴进行叉乘，得出一个方向的轴，以此类推， 代码局部实现： // 向上的向量 const vectorNormalUp = new Cartesian3(); const vZ = new
cesium加载3dtiles模型时，对3dtiles模型进行平移
qq_40437666的博客
02-20 1017
其中，targetLongitude和targetLatitude分别是需要平移到的经度和纬度。在上面的示例代码中，3dtiles会被平移到目标的经度和纬度上，并且最低点的高度也会被设置为0.当我们使用cesium加载3dtiles模型时，有时模型并没有加载在正确的位置上，这时我们就需要对模型的经纬度和高度进行平移。
cesium加载3dtiles格式的倾斜摄影模型数据
05-03
6. **交互功能**：Cesium提供了丰富的交互功能，用户可以通过鼠标或触摸设备进行旋转、平移、缩放等操作，查看3D模型的不同角度和细节。 7. **应用场景**：结合倾斜摄影模型数据，Cesium可以用于城市规划展示、建筑...
Cesium中级开发教程之三十：3DTiles旋转平移
Cesium开发工程师
02-09 355
它能够高效地管理和展示如城市建筑、地形、三维模型等大规模 3D 数据，通过将数据分块组织，实现按需加载和渲染，提高了数据处理和显示的效率。在对 3DTiles 数据进行可视化展示时，旋转、缩放和平移操作是常见且重要的交互方式，能够帮助用户从不同角度、距离和位置观察 3D 场景。旋转矩阵是一个 3×3 或 4×4 的矩阵，它可以将一个向量在三维空间中进行旋转变换；通过平移矩阵来实现，平移矩阵是一个 4×4 的矩阵，其作用是将模型在 X、Y、Z 三个坐标轴方向上分别移动一定的距离。4、3DTiles旋转平移。
3dtiles模型的旋转平移
01-07
cesium 3dtiles模型的旋转平移
Cesium模型调整
12-22
大家下载了之后，把资源替换成你本地的，然后看下控制台，有的方法得自己改下，别再问为啥跑不了了。
Cesium 平移cesiumlab生产的3Dtiles切片模型到目标经纬度
weixin_43056496的博客
07-30 948
在没有cesiumlab官方授权的情况下，用cesiumlab的生产的切片模型数据，默认与实际位置有距离偏差，不能只通过平移矩阵移动模型到实际位置，还需要对应的旋转矩阵。本篇文章将通过cesium的内置函数，将模型移动到实际位置。
Cesium17-3DTileset模型旋转平移
m0_56492004的博客
03-19 825
定义两个全局变量，cartographic，params，用于计算模型的初始位置和存储旋转平移参数。
cesium 局部加载_Cesium 中的图形变换：局部平移、缩放、旋转思路及代码实现
weixin_36242060的博客
01-26 829
开门见山：tileset.modelMatrix这个属性可以在数据本身的基础上再进行坐标变换，不熟悉转换矩阵各个部分的含义的可参考图形学有关资料。此文不一定是最佳算法，但是提供一种思路。转载请注明出处 全网@秋意正寒 。平移思路获取当前瓦片数据集的包裹范围(boundingSphere)中心(此时参考系是世界坐标)计算当参考系是局部坐标时，此位置为原点的局部坐标系，到世界坐标的转换矩阵(eastN...
Cesium--旋转3dtiles
LongJ_Sir的博客
06-25 502
记录-来自论坛的3dtiles旋转
cesium 3DTileset的平移、旋转、缩放
D_bel的博客
04-14 3435
Cesium.Transforms.eastNorthUpToFixedFrame方法是得到世界坐标到某个点平移，得到变化后的矩阵。将这个值赋给_root.transform，模型就回移动旋转到指定位置。1、tileset.modelMatrix：可以用来平移，旋转好像有问题。这个方法的旋转是围绕地球，不是模型自身，旋转中心好像是在。2、tileset._root.transformcesuim：加载的模型的旋转矩阵似乎储存在_root.transform里面的。中心，平移感觉又在模型本身中心。
DEJA_VU3D - Cesium功能集：编辑gltf模型的平移和旋转
AbjCommon_Lisp的博客
09-17 893
通过以上代码示例，我们可以看到如何使用DEJA_VU3D - Cesium功能集来实现gltf模型的平移和旋转操作。在本文中，我们将探讨如何使用DEJA_VU3D - Cesium功能集来编辑gltf模型的平移和旋转。在上述代码中，我们同样首先创建了一个Cesium的Viewer实例，并加载了一个gltf模型。在上述代码中，我们首先创建了一个Cesium的Viewer实例，并加载了一个gltf模型。接下来，我们将介绍如何使用DEJA_VU3D - Cesium来实现平移和旋转操作，并提供相应的源代码示例。
Cesium模型旋转
05-25
### Cesium 中实现模型旋转的方法 在 Cesium 中，可以通过多种方式实现模型的旋转操作。以下是常见的几种方法及其具体实现： #### 方法一：通过 `modelGraphics` 设置欧拉角 Cesium 提供了 `Entity.modelGraphics` 对象用于加载 GLTF 或 GLB 模型，并允许设置模型的方向（orientation）。方向可以通过欧拉角（Euler angles）定义，从而控制模型绕三个轴的旋转。 ```javascript var viewer = new Cesium.Viewer('cesiumContainer'); var entity = viewer.entities.add({ position : Cesium.Cartesian3.fromDegrees(-75.0, 40.0, 300000.0), model : { uri : 'path/to/model.gltf', scale : 1.0, minimumPixelSize : 128, maximumScale : 2.0, orientation : Cesium.Transforms.headingPitchRollQuaternion( Cesium.Cartesian3.fromDegrees(-75.0, 40.0, 300000.0), Cesium.Math.toRadians(45), // heading (yaw) Cesium.Math.toRadians(30), // pitch Cesium.Math.toRadians(15) // roll ) } }); viewer.zoomTo(entity); ``` 此代码片段展示了如何利用 `headingPitchRollQuaternion` 函数指定模型的朝向[^1]。 --- #### 方法二：使用 `Matrix3` 进行精确旋转 对于更复杂的场景，可以直接使用 Cesium 的矩阵工具类 `Cesium.Matrix3` 来创建自定义旋转矩阵。这种方法适用于需要单独调整 X、Y 和 Z 轴旋转角度的情况。 ```javascript var viewer = new Cesium.Viewer('cesiumContainer'); var scene = viewer.scene; // 创建一个实体并附加模型 var entity = viewer.entities.add({ position: Cesium.Cartesian3.fromDegrees(-75.0, 40.0, 300000.0), model: { uri: 'path/to/model.glb' } }); viewer.trackedEntity = entity; // 获取模型实例 var modelPrimitive = scene.primitives.get(scene.primitives.length - 1); if (modelPrimitive && modelPrimitive.readyPromise) { modelPrimitive.readyPromise.then(function(model) { var rotationX = Cesium.Matrix3.fromRotationX(Cesium.Math.toRadians(45)); // 绕X轴旋转45° var rotationY = Cesium.Matrix3.fromRotationY(Cesium.Math.toRadians(30)); // 绕Y轴旋转30° var rotationZ = Cesium.Matrix3.fromRotationZ(Cesium.Math.toRadians(15)); // 绕Z轴旋转15° // 合并旋转矩阵 var finalRotation = Cesium.Matrix3.multiply(rotationX, rotationY, new Cesium.Matrix3()); finalRotation = Cesium.Matrix3.multiply(finalRotation, rotationZ, finalRotation); // 应用到模型根节点 model._root.transform = Cesium.Matrix4.fromRotationTranslation(finalRotation); }); } ``` 该示例说明了如何组合多个旋转矩阵以完成复杂变换[^3]。 --- #### 方法三：基于 CZML 动态更新模型姿态 CZML 是一种描述动态数据的语言，在其中可以定义模型的姿态变化（articulations），并通过时间序列动画化这些变化。 ```json { "id": "document", "name": "Model Rotation Example", "version": "1.0" }, { "id": "modelNode", "position": {"cartographicDegrees": [-75.0, 40.0, 30000]}, "model": { "uri": "path/to/model.gltf", "scale": 1.0 }, "articulations": [ { "id": "rotateAroundX", "value": [{"time": "2023-01-01T00:00:00Z", "numberValue": 0}, {"time": "2023-01-01T00:01:00Z", "numberValue": 90}] } ] } ``` 在此配置中，`articulations` 定义了一个围绕 X 轴的时间依赖性旋转[^2]。 --- #### 方法四：通过 Primitive API 控制高级行为 当需要完全掌控模型的行为时，可直接操作底层 Primitive 层级的对象。这种方式提供了最大的灵活性，但也增加了开发难度。 ```javascript var viewer = new Cesium.Viewer('cesiumContainer'); var primitiveCollection = viewer.scene.primitives; var modelMatrix = Cesium.Transforms.eastNorthUpToFixedFrame( Cesium.Cartesian3.fromDegrees(-75.0, 40.0, 300000.0)); var rotationAngle = Cesium.Math.toRadians(45); // 旋转角度 var rotationMatrix = Cesium.Matrix3.fromRotationZ(rotationAngle); var combinedTransform = Cesium.Matrix4.fromRotationTranslation(rotationMatrix); primitiveCollection.add(new Cesium.ModelPrimitive({ modelMatrix: combinedTransform, url: 'path/to/model.glb' })); ``` 这段代码演示了如何手动构建完整的转换矩阵并将它应用至模型原始对象[^4]。 --- ### 总结 以上四种方法分别适合不同的应用场景： - **方法一**：快速简单的静态旋转。 - **方法二**：灵活定制化的多轴联合旋转。 - **方法三**：支持动态效果和时间线驱动的交互式体验。 - **方法四**：低级别精细操控需求下的首选方案。 每种技术都有其适用范围，请根据实际项目需求选择合适的解决方案。
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值