四轴联动系统综合误差建模
背景介绍
如图为测量系统,测量系统为一个四轴联动系统,整个装置可以抽象为测量件运动链和探头运动链组成的系统,具有X,Y,Z三个平动轴以及B轴一个转动轴组成的系统。传动关系为叶片-B-X-Y-Z-色散探头。

D-H 齐次坐标变换
D-H 齐次坐标变换是由Denavit-Hartenberg提出的一种通用坐标变换方法,常用于建立机械臂的运动学模型。
测量系统几何误差分析
根据测量系统几何误差分析,该测量系统床共有31项几何误差,如表所示。
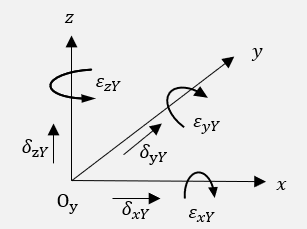
δ
n
M
δ_nM
δnM表示平动误差,
ε
n
M
ε_nM
εnM表示角度误差,下标的第一个字母以小写字母表示误差的运动或者旋转方向的轴,如 x 轴、y 轴和 z 轴;下标的第二个字母以大写字母表示运动轴,如 X轴、Z轴、Z轴和 B 轴。
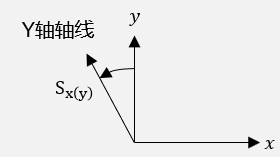
S
i
(
j
)
S_i (j)
Si(j)表示在 j轴上 i 方向的垂直度误差。

运用多体系统理论和齐次坐标变换理论建立测量系统运动综合误差模型, 可以对测量系统的各项误差元进行综合考虑与分析,并能对各项误差元之间的耦合关系进行分析与解耦。多体系统理论是在实际建模过程中,对于测量系统的运动采用低序体阵列的方法进行多体系统拓扑结构描述,如图所示。采用齐次特征矩阵表示各部件之间的几何特征,计算出探头在被测件坐标系中的姿态和位置坐标,从而建立实际测量运动模态,完成测量系统的运动综合误差建模。
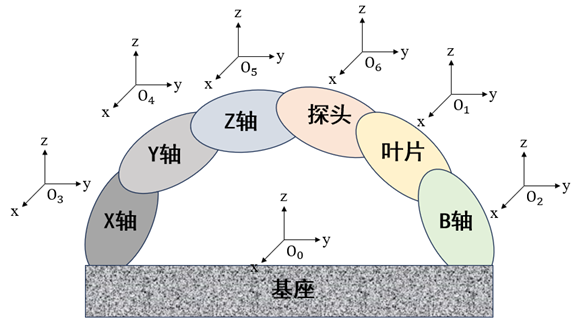
建立测量系统坐标系,基于多体理论推导机床误差综合数学模型,为计算被测件和探头之间的误差和为测量系统建模方便,所有测量系统构件坐标系都采用右手笛卡尔坐标系。测量系统分为两条运动链。被测物链:在被测件上建立坐标系1为低序体 1;在 B 轴转台上建立坐标系 2为低序体2。探头链:在测量系统基座上建立参考坐标系 0;在 X轴平动轴上建立坐标系 3 为低序体 3;在 Y 轴主轴上建立坐标系 4为低序体4;在Z轴上建立坐标系5 为低序体5。在探头建立上建立坐标系6为低序体6。
在建模过程中,规定测量系统误差变换矩阵的方向从被测件坐标系变换到探头坐标系,而误差因素则主要有转角误差、垂直度误差以及移动误差等,在实际测量的过程中如果出现了测量结果与规定相反,则以负值进行赋值并且进行综合计算。
测量系统几何误差建模
整体建模思路
分别列出理想(无误差)状态下相邻体间的转换矩阵和实际状态(有误差)状态下相邻体间的转换阵,通过矩阵相减得到测量系统综合误差。
理想(无误差)状态下相邻体间的转换矩阵
在理想情况下,设 X X X、 Y Y Y、 Z Z Z 平动轴的移动距离分别为 x x x、 y y y、 z z z,旋转轴 C C C 轴和 B B B 轴的旋转角度分别为 θ B \theta_B θB。
从被测物坐标系1到
B
B
B旋转轴坐标系2的齐次变换矩阵为:
B
W
T
i
=
I
{}_B^W T^i = I
BWTi=I
从
B
B
B旋转轴坐标系2到基座上建立参考坐标系0的齐次变换矩阵为:
O
B
T
i
=
[
cos
θ
B
−
sin
θ
B
0
0
sin
θ
B
cos
θ
B
0
0
0
0
1
0
0
0
0
1
]
{}_O^B T^i = \begin{bmatrix} \cos\theta_B & -\sin\theta_B & 0 & 0 \\ \sin\theta_B & \cos\theta_B & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
OBTi=
cosθBsinθB00−sinθBcosθB0000100001
从床身坐标系0到
X
X
X平动轴坐标系3的齐次变换矩阵为:
X
O
T
i
=
[
1
0
0
x
0
1
0
0
0
0
1
0
0
0
0
1
]
{}_X^O T^i = \begin{bmatrix} 1 & 0 & 0 & x \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
XOTi=
100001000010x001
从
X
X
X平动轴坐标系3到
Y
Y
Y平动轴坐标系4的齐次变换矩阵为:
Y
X
T
i
=
[
1
0
0
0
0
1
0
y
0
0
1
0
0
0
0
1
]
{}_Y^X T^i = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & y \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
YXTi=
1000010000100y01
从
Y
Y
Y平动轴坐标系4到
Z
Z
Z平动轴坐标系5的齐次变换矩阵为:
Z
Y
T
i
=
[
1
0
0
0
0
1
0
0
0
0
1
z
0
0
0
1
]
{}_Z^Y T^i = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \end{bmatrix}
ZYTi=
10000100001000z1
从
Z
Z
Z平动轴坐标系5到探头坐标系6的齐次变换矩阵为:
T
Z
T
i
=
I
{}_T^Z T^i = I
TZTi=I
那么,从被测物坐标系到探头坐标系的运动误差矩阵为:
T
W
T
i
=
B
W
T
i
⋅
0
B
T
i
⋅
X
0
T
i
⋅
Y
X
T
i
⋅
Z
Y
T
i
⋅
T
Z
T
i
{}_T^W T^i = {}_B^W T^i \cdot {}_0^B T^i \cdot {}_X^0 T^i \cdot {}_Y^X T^i \cdot {}_Z^Y T^i \cdot {}_T^Z T^i
TWTi=BWTi⋅0BTi⋅X0Ti⋅YXTi⋅ZYTi⋅TZTi
实际状态(有误差)状态下相邻体间的转换阵
与理想情况类似,设 X X X、 Y Y Y、 Z Z Z 平动轴的移动距离分别 x x x、 y y y、 z z z,旋转轴 C C C 轴和 B B B 轴的旋转角度分别为 θ B \theta_B θB。并把表2-1所示的各个运动轴的六自由度误差及轴间位置误差共计31项误差元考虑进来。
其中:
δ
i
(
j
)
\delta_i (j)
δi(j) 表示在
j
j
j 轴上
i
i
i 方向的位置误差;
ε
i
(
j
)
\varepsilon_i (j)
εi(j) 表示在
j
j
j 轴上
i
i
i 方向的角度误差;
S
i
(
j
)
S_i (j)
Si(j) 表示在
j
j
j 轴上
i
i
i 方向的垂直度误差;
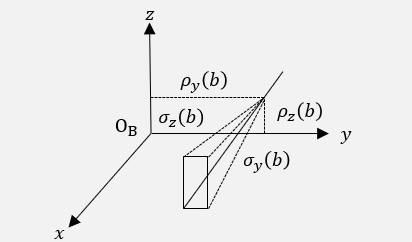
ρ
u
(
v
)
\rho_u (v)
ρu(v) 表示在
v
v
v 轴上
u
u
u 方向的位置误差;
σ
u
(
v
)
\sigma_u (v)
σu(v) 表示在
v
v
v 轴上
u
u
u 方向的角度误差;
i
i
i、
j
j
j、
u
u
u、
v
v
v 可表示为
x
x
x、
y
y
y、
z
z
z、
b
b
b。
从被测物坐标系1到B旋转轴坐标系2的齐次变换矩阵为:
B
W
T
e
=
I
[
1
−
ε
z
(
B
)
ε
y
(
B
)
+
σ
x
(
b
)
δ
x
(
B
)
+
ρ
x
(
b
)
ε
z
(
B
)
1
−
ε
x
(
B
)
−
σ
y
(
b
)
δ
y
(
B
)
+
ρ
y
(
b
)
−
ε
y
(
B
)
−
σ
x
(
b
)
ε
x
(
B
)
+
σ
y
(
b
)
1
δ
z
(
B
)
0
0
0
1
]
{}_B^W T^e = I \begin{bmatrix} 1 & -\varepsilon_z(B) & \varepsilon_y(B) + \sigma_x(b) & \delta_x(B) + \rho_x(b) \\ \varepsilon_z(B) & 1 & -\varepsilon_x(B) - \sigma_y(b) & \delta_y(B) + \rho_y(b) \\ -\varepsilon_y(B) - \sigma_x(b) & \varepsilon_x(B) + \sigma_y(b) & 1 & \delta_z(B) \\ 0 & 0 & 0 & 1 \end{bmatrix}
BWTe=I
1εz(B)−εy(B)−σx(b)0−εz(B)1εx(B)+σy(b)0εy(B)+σx(b)−εx(B)−σy(b)10δx(B)+ρx(b)δy(B)+ρy(b)δz(B)1
从B旋转轴坐标系2到基座上建立参考坐标系0的齐次变换矩阵为:
O
B
T
e
=
[
cos
θ
B
−
sin
θ
B
0
0
sin
θ
B
cos
θ
B
0
0
0
0
1
0
0
0
0
1
]
{}_O^B T^e = \begin{bmatrix} \cos\theta_B & -\sin\theta_B & 0 & 0 \\ \sin\theta_B & \cos\theta_B & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
OBTe=
cosθBsinθB00−sinθBcosθB0000100001
从床身坐标系0到X平动轴坐标系3的齐次变换矩阵为:
X
O
T
e
=
[
1
0
0
x
0
1
0
0
0
0
1
0
0
0
0
1
]
[
1
−
ε
z
(
X
)
ε
y
(
X
)
δ
x
(
X
)
ε
z
(
X
)
1
−
ε
x
(
X
)
δ
y
(
X
)
−
ε
y
(
X
)
ε
x
(
X
)
1
δ
z
(
X
)
0
0
0
1
]
{}_X^O T^e = \begin{bmatrix} 1 & 0 & 0 & x \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & -\varepsilon_z(X) & \varepsilon_y(X) & \delta_x(X) \\ \varepsilon_z(X) & 1 & -\varepsilon_x(X) & \delta_y(X) \\ -\varepsilon_y(X) & \varepsilon_x(X) & 1 & \delta_z(X) \\ 0 & 0 & 0 & 1 \end{bmatrix}
XOTe=
100001000010x001
1εz(X)−εy(X)0−εz(X)1εx(X)0εy(X)−εx(X)10δx(X)δy(X)δz(X)1
从X平动轴坐标系3到Y平动轴坐标系4的齐次变换矩阵为:
Y
X
T
e
=
[
1
0
0
0
0
1
0
y
0
0
1
0
0
0
0
1
]
[
1
−
ε
z
(
Y
)
ε
y
(
Y
)
δ
x
(
Y
)
−
y
S
x
(
y
)
ε
z
(
Y
)
1
−
ε
x
(
Y
)
δ
y
(
Y
)
−
ε
y
(
Y
)
ε
x
(
Y
)
1
δ
z
(
Y
)
0
0
0
1
]
{}_Y^X T^e = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & y \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & -\varepsilon_z(Y) & \varepsilon_y(Y) & \delta_x(Y) - yS_x(y) \\ \varepsilon_z(Y) & 1 & -\varepsilon_x(Y) & \delta_y(Y) \\ -\varepsilon_y(Y) & \varepsilon_x(Y) & 1 & \delta_z(Y) \\ 0 & 0 & 0 & 1 \end{bmatrix}
YXTe=
1000010000100y01
1εz(Y)−εy(Y)0−εz(Y)1εx(Y)0εy(Y)−εx(Y)10δx(Y)−ySx(y)δy(Y)δz(Y)1
从Y平动轴坐标系4到Z平动轴坐标系5的齐次变换矩阵为:
Z
Y
T
e
=
[
1
0
0
0
0
1
0
0
0
0
1
z
0
0
0
1
]
[
1
−
ε
z
(
Z
)
ε
y
(
Z
)
δ
x
(
Z
)
−
z
S
x
(
z
)
ε
z
(
Z
)
1
−
ε
x
(
Z
)
δ
y
(
Z
)
−
z
S
y
(
z
)
−
ε
y
(
Z
)
ε
x
(
Z
)
1
δ
z
(
Z
)
0
0
0
1
]
{}_Z^Y T^e = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & -\varepsilon_z(Z) & \varepsilon_y(Z) & \delta_x(Z) - zS_x(z) \\ \varepsilon_z(Z) & 1 & -\varepsilon_x(Z) & \delta_y(Z) - zS_y(z) \\ -\varepsilon_y(Z) & \varepsilon_x(Z) & 1 & \delta_z(Z) \\ 0 & 0 & 0 & 1 \end{bmatrix}
ZYTe=
10000100001000z1
1εz(Z)−εy(Z)0−εz(Z)1εx(Z)0εy(Z)−εx(Z)10δx(Z)−zSx(z)δy(Z)−zSy(z)δz(Z)1
从Z平动轴坐标系5到探头坐标系6的齐次变换矩阵为:
T
Z
T
e
=
I
{}_T^Z T^e = I
TZTe=I
那么,从被测物坐标系到探头坐标系的运动误差矩阵为:
T
W
T
e
=
B
W
T
e
⋅
0
B
T
e
⋅
X
0
T
e
⋅
Y
X
T
e
⋅
Z
Y
T
e
⋅
T
Z
T
e
{}_T^W T^e = {}_B^W T^e \cdot {}_0^B T^e \cdot {}_X^0 T^e \cdot {}_Y^X T^e \cdot {}_Z^Y T^e \cdot {}_T^Z T^e
TWTe=BWTe⋅0BTe⋅X0Te⋅YXTe⋅ZYTe⋅TZTe
最后运算
基于小误差假设理论,测量系统空间运动综合误差变换矩阵
T
W
E
{}_T^W E
TWE 可表示为:
T
W
E
=
T
W
T
e
−
T
W
T
i
=
[
1
−
Δ
ε
z
Δ
ε
y
Δ
x
Δ
ε
z
1
−
Δ
ε
x
Δ
y
−
Δ
ε
y
Δ
ε
x
1
Δ
z
0
0
0
1
]
{}_T^W E = {}_T^W T^e - {}_T^W T^i = \begin{bmatrix} 1 & -\Delta\varepsilon_z & \Delta\varepsilon_y & \Delta x \\ \Delta\varepsilon_z & 1 & -\Delta\varepsilon_x & \Delta y \\ -\Delta\varepsilon_y & \Delta\varepsilon_x & 1 & \Delta z \\ 0 & 0 & 0 & 1 \end{bmatrix}
TWE=TWTe−TWTi=
1Δεz−Δεy0−Δεz1Δεx0Δεy−Δεx10ΔxΔyΔz1
式中 Δ x \Delta x Δx、 Δ y \Delta y Δy、 Δ z \Delta z Δz 是探头实际位移点相对理想指令位移点的移动误差。 Δ ε x \Delta\varepsilon_x Δεx、 Δ ε y \Delta\varepsilon_y Δεy、 Δ ε z \Delta\varepsilon_z Δεz 为探头实际位置相对理想指令位置的转角误差。
基于小误差假设,忽略二阶及二阶以上小量,可得 Δ x \Delta x Δx、 Δ y \Delta y Δy、 Δ z \Delta z Δz 的表达式。
MATLAB编程仿真
clc
clear
% 使用符号计算
syms x y z % 平移距离
syms theta_B % 旋转角度
% 定义齐次变换矩阵
WB_Ti = eye(4); % 从被测物坐标系1到B旋转轴坐标系2的齐次变换矩阵为单位矩阵
B0_Ti = [cos(theta_B) -sin(theta_B) 0 0; sin(theta_B) cos(theta_B) 0 0; 0 0 1 0; 0 0 0 1]; % 从B旋转轴坐标系2到基座上建立参考坐标系0的齐次变换矩阵
X0_Ti = [1 0 0 x; 0 1 0 0; 0 0 1 0; 0 0 0 1]; % 从床身坐标系0到X平动轴坐标系3的齐次变换矩阵
XY_Ti = [1 0 0 0; 0 1 0 y; 0 0 1 0; 0 0 0 1]; % 从X平动轴坐标系3到Y平动轴坐标系4的齐次变换矩阵
YZ_Ti = [1 0 0 0; 0 1 0 0; 0 0 1 z; 0 0 0 1]; % 从Y平动轴坐标系4到Z平动轴坐标系5的齐次变换矩阵
ZT_Ti = eye(4); % 从Z平动轴坐标系5到探头坐标系6的齐次变换矩阵为单位矩阵
% 计算总的变换矩阵
WT_Ti = WB_Ti * B0_Ti * X0_Ti * XY_Ti * YZ_Ti * ZT_Ti;
% 显示结果
disp('从被测物坐标系到探头坐标系的运动误差矩阵为:');
disp(WT_Ti);
% 使用符号计算
syms ezB exB eyB deltaxB deltayB deltazB exX eyX ezX deltaxX deltayX deltazX exY eyY ezY deltaxY deltayY deltazY exZ eyZ ezZ deltaxZ deltayZ deltazZ
syms Sxy Sxz Syz rhox_b rhoy_b sigmax_b sigmay_b
syms theta_B x y z
% 定义齐次变换矩阵
WB_Te = [1 -ezB eyB+sigmax_b deltaxB+rhox_b;
ezB 1 -exB-sigmay_b deltayB+rhoy_b;
-eyB-sigmax_b exB+sigmay_b 1 deltazB;
0 0 0 1];
B0_Te = [cos(theta_B) -sin(theta_B) 0 0;
sin(theta_B) cos(theta_B) 0 0;
0 0 1 0;
0 0 0 1];
X0_Te = [1 0 0 x;
0 1 0 0;
0 0 1 0;
0 0 0 1] * [1 -ezX eyX deltaxX;
ezX 1 -exX deltayX;
-eyX exX 1 deltazX;
0 0 0 1];
XY_Te = [1 0 0 0;
0 1 0 y;
0 0 1 0;
0 0 0 1] * [1 -ezY eyY deltaxY-y*Sxy;
ezY 1 -exY deltayY;
-eyY exY 1 deltazY;
0 0 0 1];
YZ_Te = [1 0 0 0;
0 1 0 0;
0 0 1 z;
0 0 0 1] * [1 -ezZ eyZ deltaxZ-z*Sxz;
ezZ 1 -exZ deltayZ-z*Syz;
-eyZ exZ 1 deltazZ;
0 0 0 1];
ZT_Te = eye(4); % 从Z平动轴坐标系5到探头坐标系6的齐次变换矩阵为单位矩阵
% 计算总的变换矩阵
WT_Te = WB_Te * B0_Te * X0_Te * XY_Te * YZ_Te * ZT_Te;
% 显示结果
disp('从被测物坐标系到探头坐标系的运动误差矩阵为:');
disp(WT_Te);
WTE = WT_Te - WT_Ti;
% 显示结果
disp('从被测物坐标系到探头坐标系的误差矩阵 WTE 为:');
disp(WTE);
syms deltay_x deltay_y deltay_z;
deltay_x=WTE(1,4);
deltay_y=WTE(2,4);
deltay_z=WTE(3,4);
disp(deltay_x);
disp(deltay_y);
disp(deltay_z);
写在后面
之前对测量系统的综合误差进行了建模,但整个分析过程仍存在一些问题,后续会进行修正,先把已有的进度记录下来。
——RIVER CHEN(2025.9.24于华中科技大学)
附
“无论走到哪里都应该记住,过去都是假的,回忆是一条没有归途的路,以往的一切春天都无法复原,即使最狂乱且坚韧的爱情,归根结底也不过是一种瞬息即逝的现实,唯有孤独永恒。”
——《百年孤独》





















 3152
3152

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








