Sobol灵敏度分析的讲述及matlab实现
Sobol灵敏度分析的原理
灵敏度分析包括局部灵敏度分析和全局灵敏度分析2种方法。局部灵敏度分析方法仅考虑单个误差项的变化对空间误差的影响,忽略了几何误差各项之间的耦合作用; 而全局灵敏度分析方法考虑了各个误差项之间的耦合作用对空间误差的影响。在测量系统几何误差中,各个误差项之间的耦合作用不可忽略,故文中使用全局灵敏度分析的方法。
Sobol 法作为一种常见的全局灵敏度分析方法,原理如下:
假设空间误差
E
E
E 是关于误差项
x
1
,
x
2
,
…
,
x
k
x_1, x_2, \dots, x_k
x1,x2,…,xk 的函数表达式:
E
=
f
(
x
1
,
x
2
,
…
,
x
k
)
E = f(x_1, x_2, \dots, x_k)
E=f(x1,x2,…,xk)
误差函数
f
(
x
)
f(\mathbf{x})
f(x) 方差分析式可表示为
f
(
x
1
,
x
2
,
…
,
x
k
)
=
f
0
+
∑
i
f
i
(
x
i
)
+
∑
i
<
j
f
i
j
(
x
i
,
x
j
)
+
⋯
+
f
1
…
k
(
x
1
,
x
2
,
…
,
x
k
)
f(x_1, x_2, \dots, x_k) = f_0 + \sum_{i} f_i(x_i) + \sum_{i<j} f_{ij}(x_i, x_j) + \cdots + f_{1\dots k}(x_1, x_2, \dots, x_k)
f(x1,x2,…,xk)=f0+i∑fi(xi)+i<j∑fij(xi,xj)+⋯+f1…k(x1,x2,…,xk)
其中
f
0
f_0
f0 为常数项,各子项对其所包含的任一因素的积分都为 0,即
∫
f
i
1
i
2
…
i
s
(
x
i
1
,
x
i
2
,
…
,
x
i
s
)
d
x
k
=
0
(
k
=
i
1
,
i
2
,
…
,
i
s
)
\int f_{i_1 i_2 \dots i_s} (x_{i_1}, x_{i_2}, \dots, x_{i_s}) \, dx_k = 0 \quad (k = i_1, i_2, \dots, i_s)
∫fi1i2…is(xi1,xi2,…,xis)dxk=0(k=i1,i2,…,is)
另外,式中各子项之间正交,各阶子项的值可表示为
f
(
x
)
f(\mathbf{x})
f(x) 积分。
误差函数输出总方差:
D
=
∫
f
2
(
x
)
d
x
−
f
0
2
=
∑
s
=
1
n
∑
i
1
<
⋯
<
i
s
∫
f
i
1
i
2
…
i
s
2
(
x
i
1
,
x
i
2
,
…
,
x
i
s
)
d
x
i
1
…
d
x
i
s
\begin{aligned} D &= \int f^2(\mathbf{x}) \, d\mathbf{x} - f_0^2 \\ &= \sum_{s=1}^{n} \sum_{i_1 < \dots < i_s} \int f_{i_1 i_2 \dots i_s}^2 (x_{i_1}, x_{i_2}, \dots, x_{i_s}) \, dx_{i_1} \dots dx_{i_s} \end{aligned}
D=∫f2(x)dx−f02=s=1∑ni1<⋯<is∑∫fi1i2…is2(xi1,xi2,…,xis)dxi1…dxis
其中:
D
i
1
i
2
…
i
s
=
∫
f
i
1
i
2
…
i
s
2
(
x
i
1
,
x
i
2
,
…
,
x
i
s
)
d
x
i
1
…
d
x
i
s
(
1
≤
i
1
<
⋯
<
i
s
≤
k
)
\begin{aligned} &D_{i_1 i_2 \dots i_s} = \int f_{i_1 i_2 \dots i_s}^2 (x_{i_1}, x_{i_2}, \dots, x_{i_s}) \, dx_{i_1} \dots dx_{i_s} \\ &(1 \leq i_1 < \dots < i_s \leq k) \end{aligned}
Di1i2…is=∫fi1i2…is2(xi1,xi2,…,xis)dxi1…dxis(1≤i1<⋯<is≤k)
定义比值:
S
i
1
i
2
…
i
s
=
D
i
1
i
2
…
i
s
D
(
1
≤
i
1
<
⋯
<
i
s
≤
k
)
S_{i_1 i_2 \dots i_s} = \frac{D_{i_1 i_2 \dots i_s}}{D} \quad (1 \leq i_1 < \dots < i_s \leq k)
Si1i2…is=DDi1i2…is(1≤i1<⋯<is≤k)
其中:
S
i
S_i
Si 为误差项
x
i
x_i
xi 的一阶灵敏度系数,表示误差项
x
i
x_i
xi 对空间误差的影响程度;
S
i
j
S_{ij}
Sij 为二阶灵敏度系数 (
i
,
j
i,j
i,j 不同时为
i
1
,
…
,
i
s
i_1, \dots, i_s
i1,…,is),表示误差项
x
i
,
x
j
x_i, x_j
xi,xj 耦合对空间误差的影响程度;其他依此类推。
定义总体灵敏度系数:
S
T
i
=
1
−
D
−
i
D
S_{T_i} = 1 - \frac{D_{-i}}{D}
STi=1−DD−i
总体灵敏度系数表示误差项
x
i
x_i
xi 的一阶灵敏度系数
S
i
S_i
Si 和所有与
x
i
x_i
xi 有耦合作用的高阶灵敏度系数之和。
灵敏度系数可以用于判别系统或模型输出对输入参数变化的敏感程度。如果灵敏度系数较大,说明输出
Y
Y
Y 对输入
X
X
X 的变化非常敏感,即使输入
X
X
X 只有微小的变化,也会导致输出
Y
Y
Y 的显著变化。
Sobol灵敏度分析的Matlab实现
对例程来源验证,进行matlab编程实现
参考https://blog.youkuaiyun.com/xiaosebi1111/article/details/46517409.
使用sobol灵敏度分析方法,利用matlab对下式进行了分析
y
=
sin
(
x
1
)
+
7
×
(
sin
(
x
2
)
)
2
+
0.1
×
x
3
4
×
sin
(
x
1
)
y = \sin(x_1) + 7 \times (\sin(x_2))^2 + 0.1 \times x_3^4 \times \sin(x_1)
y=sin(x1)+7×(sin(x2))2+0.1×x34×sin(x1)
%sobol 参数敏感性分析
%参考文章https://blog.csdn.net/xiaosebi1111/article/details/46517409
%代码来源https://www.bilibili.com/video/BV1LRV7eTEEP/?spm_id_from=333.337.search-card.all.click&vd_source=7a0104e4fb1279699dc3e1a3ef4989fa
%运行环境 matlab2024a
%代码修改 RIVER CHEN
%%初始化
clc;
clear all
%设定:给定参数个数和各个参数得范围
D=3;%维度,几个参数
M=D*2;
nPop=4;%采样点个数,也就是参数水平数,取大了好,比如4000.但慢
% nPop=4000;
VarMin=[0 0 0];%各个参数下限
VarMax=[1 1 1];%各个参数上限
% %产生所需得各个水平参数
VarMin=[VarMin,VarMin];
VarMax=[VarMax,VarMax];
p=sobolset(M);%利用MATLAB统计工具箱中的 “Sobolset” 函数,生成Sobol 序列
%R=p(:nPop,:);%我只用前nPop个
R=[];
for i=1:nPop
r=p(i,:);
r=VarMin+r.*(VarMax-VarMin);
R=[R;r];
end
% plot(R(:,1),'b*')
%%
%拆分为A B
% A=R(:,1:D);%每行代表一组参数,其中每列代表每组参数得一个参数;行数就代表共有几组参数
% B=R(:,D+1:end);
% 根据A B产生矩阵AB————用B的第i列替换A中的第i列产生新的矩阵ABi,存于AB三维矩阵中
% AB=zeros(nPop,D,D);
% for i=1:D
% tempA=A;
% tempA(:,i)=B(:,i);
% AB(1:nPop,1:D,i)=tempA;
% end
% DY______优快云验算
A=[0.5,0.5,0.5;0.75,0.25,0.25;0.25,0.75,0.75;0.375,0.375,0.625];
B=[0.5,0.5,0.5;0.25,0.75,0.75;0.75,0.25,0.25;0.875,0.375,0.125];
%根据A B产生矩阵AB——————————用B的第i列替换A中的第i列产生新的矩阵ABi,存于AB三维矩阵中
AB=zeros(nPop,D,D);
for i=1:D
tempA=A;
tempA(:,i)=B(:,i);
AB(1:nPop,1:D,i)=tempA;
end
% 求各参数解
YA=zeros(nPop,1);
YB=zeros(nPop,1);
YAB=zeros(nPop,D);
for i=1:nPop
YA(i)=myfun(A(i,:));
YB(i)=myfun(B(i,:));
for j=1:D
YAB(i,j)=myfun(AB(i,:,j));
end
end
%%根据一阶影响指数公式:
VarX=zeros(D,1);%S的分子
S=zeros(D,1);
%0:估算基于给定样本的方差(EXCEL var.p):1:计算基于给定的样本总体的方差(EXCEL var.P())
%var([2.091363878 1.110366059 3.507651769 1.310950363 2.091363878 3.507651769 1.110366059 1.7066512],1);
VarY=var([YA;YB],1);%S的分母。 计算基于给定的样本总体方差(EXCEL var.P())
for i=1:D
for j=2:nPop
VarX(i)=VarX(i)+YB(j)*(YAB(j,i)-YA(j));
end
VarX(i)=1/nPop*VarX(i);
S(i)=VarX(i)/VarY;
end
%% 总效应指数
EX=zeros(D,1);
ST=zeros(D,1);
for i=1:D
for j=1:nPop
EX(i)=EX(i)+(YA(j)-YAB(j,i))^2;
end
EX(i)=1/(2*nPop)*EX(i);
ST(i)=EX(i)/VarY;
end
disp('一阶影响指数:S');
disp(S);
disp('总效应指数:ST');
disp(ST);
disp('success!');
%%画图数据准备
% y轴数据处理
YData=zeros(D,2);
for i=1:D
% YData(i,:)=[abs(S(i)),abs(ST(i))];
YData(i,:)=[S(i),ST(i)];
end
%% 绘制柱状图
YData = [S, ST]; % Y 轴数据
ax1 = subplot(1, 1, 1);
hBar = bar(YData, 'grouped'); % 绘制分组柱状图
% 设置坐标轴标签
xlabel('Design variable');
ylabel('Sensitivity index');
% 设置图例
lgd1 = legend('Individual (S)', 'Total (ST)', 'FontSize', 13);
lgd1.NumColumns = 1; % 图例纵向排列
function y=myfun(x)
y=sin(x(1))+7*(sin(x(2)))^2+0.1*sin(x(1))*(x(3))^4;
end
运行代码,可得如下图与数。


与https://blog.youkuaiyun.com/xiaosebi1111/article/details/46517409所得结果相符。
进一步测算
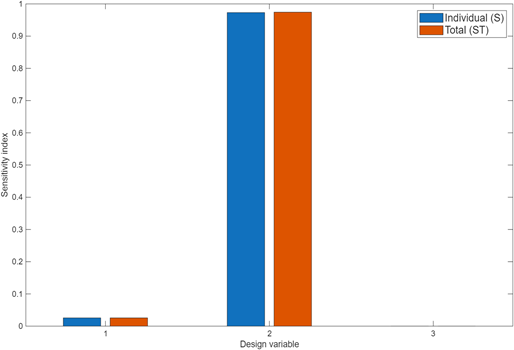
假设三个自变量的取值范围都设为[0,1],自变量数目为3(D = 3),将自变量的取值范围进行拟 Monte Carlo 采样,可利用MATLAB统计工具箱中的 “Sobolset” 函 数,生成Sobol 序列,样本矩阵误差项抽样次数 n 设定为4000。一阶影响指数表示单个输入参数对输出结果的独立贡献程度。总效应指数表示输入参数对输出结果的总贡献,包括其与其他参数的交互作用。
运行如下代码,
%sobol 参数敏感性分析
%参考文章https://blog.csdn.net/xiaosebi1111/article/details/46517409
%代码来源https://www.bilibili.com/video/BV1LRV7eTEEP/?spm_id_from=333.337.search-card.all.click&vd_source=7a0104e4fb1279699dc3e1a3ef4989fa
%运行环境 matlab2024a
%代码修改 RIVER CHEN
%%初始化
clc;
clear all
%设定:给定参数个数和各个参数得范围
D=3;%维度,几个参数
M=D*2;
%nPop=4;%采样点个数,也就是参数水平数,取大了好,比如4000.但慢
nPop=4000;
VarMin=[0 0 0];%各个参数下限
VarMax=[1 1 1];%各个参数上限
% %产生所需得各个水平参数
VarMin=[VarMin,VarMin];
VarMax=[VarMax,VarMax];
p=sobolset(M);%利用MATLAB统计工具箱中的 “Sobolset” 函数,生成Sobol 序列
%R=p(:nPop,:);%我只用前nPop个
R=[];
for i=1:nPop
r=p(i,:);
r=VarMin+r.*(VarMax-VarMin);
R=[R;r];
end
% plot(R(:,1),'b*')
%%
%拆分为A B
A=R(:,1:D);%每行代表一组参数,其中每列代表每组参数得一个参数;行数就代表共有几组参数
B=R(:,D+1:end);
% 根据A B产生矩阵AB————用B的第i列替换A中的第i列产生新的矩阵ABi,存于AB三维矩阵中
AB=zeros(nPop,D,D);
for i=1:D
tempA=A;
tempA(:,i)=B(:,i);
AB(1:nPop,1:D,i)=tempA;
end
% DY______优快云验算
%A=[0.5,0.5,0.5;0.75,0.25,0.25;0.25,0.75,0.75;0.375,0.375,0.625];
%B=[0.5,0.5,0.5;0.25,0.75,0.75;0.75,0.25,0.25;0.875,0.375,0.125];
%根据A B产生矩阵AB——————————用B的第i列替换A中的第i列产生新的矩阵ABi,存于AB三维矩阵中
% AB=zeros(nPop,D,D);
% for i=1:D
% tempA=A;
% tempA(:,i)=B(:,i);
% AB(1:nPop,1:D,i)=tempA;
% end
% 求各参数解
YA=zeros(nPop,1);
YB=zeros(nPop,1);
YAB=zeros(nPop,D);
for i=1:nPop
YA(i)=myfun(A(i,:));
YB(i)=myfun(B(i,:));
for j=1:D
YAB(i,j)=myfun(AB(i,:,j));
end
end
%%根据一阶影响指数公式:
VarX=zeros(D,1);%S的分子
S=zeros(D,1);
%0:估算基于给定样本的方差(EXCEL var.p):1:计算基于给定的样本总体的方差(EXCEL var.P())
%var([2.091363878 1.110366059 3.507651769 1.310950363 2.091363878 3.507651769 1.110366059 1.7066512],1);
VarY=var([YA;YB],1);%S的分母。 计算基于给定的样本总体方差(EXCEL var.P())
for i=1:D
for j=2:nPop
VarX(i)=VarX(i)+YB(j)*(YAB(j,i)-YA(j));
end
VarX(i)=1/nPop*VarX(i);
S(i)=VarX(i)/VarY;
end
%% 总效应指数
EX=zeros(D,1);
ST=zeros(D,1);
for i=1:D
for j=1:nPop
EX(i)=EX(i)+(YA(j)-YAB(j,i))^2;
end
EX(i)=1/(2*nPop)*EX(i);
ST(i)=EX(i)/VarY;
end
disp('一阶影响指数:S');
disp(S);
disp('总效应指数:ST');
disp(ST);
disp('success!');
%%画图数据准备
% y轴数据处理
YData=zeros(D,2);
for i=1:D
% YData(i,:)=[abs(S(i)),abs(ST(i))];
YData(i,:)=[S(i),ST(i)];
end
%% 绘制柱状图
YData = [S, ST]; % Y 轴数据
ax1 = subplot(1, 1, 1);
hBar = bar(YData, 'grouped'); % 绘制分组柱状图
% 设置坐标轴标签
xlabel('Design variable');
ylabel('Sensitivity index');
% 设置图例
lgd1 = legend('Individual (S)', 'Total (ST)', 'FontSize', 13);
lgd1.NumColumns = 1; % 图例纵向排列
function y=myfun(x)
y=sin(x(1))+7*(sin(x(2)))^2+0.1*sin(x(1))*(x(3))^4;
end
matlab分析结果如图所示,

matlab绘制一阶影响指数和总效应指数图如图所示。
写在后面
前段时间,对sobol灵敏度分析进行了学习,一直想做个总结,以便后期回顾。
——RIVER CHEN(2025.9.24于华中科技大学)





















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








