机器学习——支持向量机 （Support Vector Machine）

一、引言

1.1 什么是SVM

SVM的定义如下：

支持向量机（Support Vector Machine, SVM） 是一类按 监督学习（supervised learning） 方式对数据进行二元分类的广义线性分类器（generalized linear classifier），其决策边界是对学习样本求解的最大边距超平面（maximum-margin hyperplan）。

下面举一个二维数据的例子，在以下数据点中，对于颜色不同的点，我们可以找一条线将二者分开，以实现分类的目的。

然而，在实际应用中，我们不难发现能够区分两者的线条众多。那么，我们该选择哪一条呢？通过对比下方的两幅图，从直观感受上，右侧的线条显然优于左侧的线条。如果随机添加一些数据点，左侧的线条很有可能分错数据点，因为现有的数据点离线的距离非常的近，因此这个模型的容忍度就比较低，而右侧对比来说容忍度比较高，优于左侧。

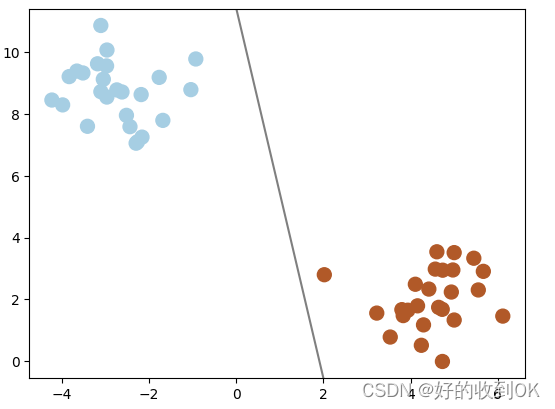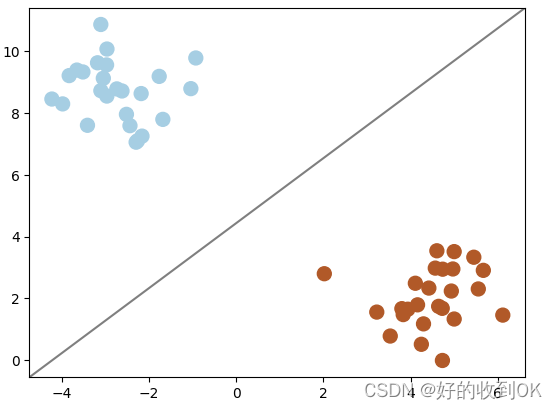那么，该如何找到最优的那一条线呢？我们需要找到一个特殊的线，这个线距离最近的数据点最远，这个线就是我们所需要的。

这就是SVM的核心思想——间隔最大，如下图，其中这条实线就是决策边界，两个圈出来的离决策边界最近的点就是支持向量，这两个支持向量到决策边界距离的和（即两条虚线之间的距离）就是间隔，而这里的间隔要优化为最大，这样得出的决策边界就是SVM所需的。

当然，上述解释都仅仅在二维数据上呈现，但SVM是可以在多维数据上实现的，例如三维上决策边界就是一个平面，n维数据的决策边界就是一个学习样本求解的最大边距超平面（n-1维）。

1.2 SVM的重要性与应用领域

1.2.1 SVM的重要性

• 分类效果和泛化能力：SVM作为一种基于统计的自然语言理解方法，具有较好的分类效果和泛化能力，可以处理高维数据和非线性数据。
• 广泛的应用场景：SVM可以应用于多种自然语言处理任务，例如文本分类、命名实体识别和情感分析等。此外，它还可以用于回归分析、异常值检测等任务。
• 可解释性：SVM具有较好的可解释性，可以通过支持向量和超平面等概念来解释分类决策的过程，使得结果更易于理解和分析。

1.2.2 SVM的应用领域

• 文本分类：SVM在文本分类领域有广泛应用，如情感分析、垃圾邮件识别、新闻分类等。通过提取文本特征并使用SVM进行分类，可以实现高效的文本分类系统。
• 图像识别：SVM在图像识别领域也表现出色，如人脸识别、物体检测、图像分类等。通过提取图像特征并使用SVM进行分类，可以实现高效且准确的图像识别系统。
• 医学诊断：在医学领域，SVM可以用于疾病诊断。通过对病人的医学图像、生化指标等数据进行特征提取，再使用SVM进行分类，可以帮助医生判断病情。
• 金融风险评估：在金融领域，SVM可以用于信用评分和风险评估。通过分析客户的财务状况、信用记录等信息，SVM可以预测客户是否具有违约风险。

1.3 SVM与其他分类算法的对比

1.3.1 核心思想

• SVM：基于最大间隔原理，寻找一个超平面将数据分为两类，同时最大化支持向量到超平面的距离。
• 逻辑回归：基于概率模型，通过最大化似然函数来实现类别之间的分离。
• 决策树：利用树形结构，根据样本属性划分节点，直到达到叶子节点，叶子节点即为类别。

1.3.2 适用性与性能

• SVM：
  • 适用性广泛：可用于各种数据类型和领域，如文本分类、图像识别等。
  • 鲁棒性强：对噪声和异常点有一定的鲁棒性。
  • 高效处理高维数据：通过核技巧将低维空间的非线性问题映射到高维空间。
  • 可避免陷入局部最优解：使用结构风险最小化原则。
• 逻辑回归：主要用于二分类问题，输出为概率值，表示样本属于某类别的概率。
• 决策树：易于理解和解释，对数据准备要求简单或不必要，能处理数据型和常规型属性。

1.3.3 劣势与限制

• SVM：
  • 计算复杂度高：在大规模数据集上的训练时间较长。
  • 参数选择敏感：需要仔细调优参数，并可能通过交叉验证来确定最佳参数。
  • 对缺失数据敏感：在含有大量缺失数据的情况下可能表现不佳。
  • 适用于二分类问题：原始SVM算法主要解决二分类问题，对多类别问题需要扩展。
• 逻辑回归：主要用于二分类问题，对于多分类问题可能需要使用其他方法。
• 决策树：可能会产生过拟合问题，特别是对于复杂数据集。

1.3.4 总结

• SVM在分类问题中因其独特的最大间隔原理、对高维数据的处理能力以及鲁棒性而备受青睐。然而，其在大规模数据集上的计算复杂度和参数敏感性是需要考虑的问题。
• 逻辑回归和决策树则分别以其概率输出和易于理解的树形结构在某些场景下有独特的优势，但也各自存在一些限制。

二、理论

2.1 线性可分与线性不可分

2.1.1 线性可分的基本概念

在二分类问题中，给定训练数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) } D = \{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\} D={ (x1​,y1​),(x2​,y2​),…,(xn​,yn​)}
其中:

1. $x_i\in {\mathbb{R}}^d$ 是 $d$ 维特征向量
2. y i ∈ { − 1 , 1 } y_i \in \{-1, 1\} yi​∈{ −1,1} 是类别标签

如果存在一个超平面 $w\cdot x+b=0$ 能够将这两类数据完全分开，即对于所有 $y_i=1$ 的数据点有 $w\cdot x_i+b>0$，对于所有 $y_i=-1$ 的数据点有 $w\cdot x_i+b<0$，则称这两类数据是线性可分的。

简单理解就是一组二类数据，如果能找到将二者分开的一个超平面，那么就是线性可分的。以下两张图中，前者是线性可分的，后者是线性不可分的，其中，后者找不到一条线来将两类数据分开。

2.1.2 线性不可分与特征空间转换

当数据在原始特征空间中不是线性可分时，可以通过一个映射函数 $\varphi (x)$ 将数据从原始空间映射到高维特征空间，然后在高维空间中寻找一个线性超平面来分隔数据。映射函数 $\varphi (x)$ 通常是通过核函数 $K(x,x^{\prime })$ 隐式定义的，即 $\varphi (x)\cdot \varphi (x^{\prime })=K(x,x^{\prime })$。

下面是一个具体例子便于理解，首先我们有一个一维的二类数据点，要将一维的数据点分类我们需要找到一个点，显然，这里找不到这样的一个点，因此这个一维数据是线性不可分的。

但是，将一维数据映射到二维之后，这里做了平方处理，就可以很容易地找到决策边界将二者分类，使得数据变得线性可分。

2.2 最优超平面

2.2.1 最优超平面的定义

在支持向量机（SVM）中，最优超平面是一个能够将训练数据集中的正负样本完全正确划分，并且使得两类样本之间的间隔达到最大的超平面。这个间隔定义为样本点到超平面的最短距离的两倍。

给定一个数据集，其中每个样本点 $x_i$ 都带有一个标签 $y_i$（通常 y i ∈ { − 1 , 1 } y_i \in \{-1, 1\} yi​∈{ −1,1} 表示不同的类别），最优超平面可以表示为：

$$w\cdot x+b=0$$

其中：

1. $w$ 是超平面的法向量
2. $b$ 是截距

2.2.2 间隔最大化的原理

在支持向量机（SVM）中，间隔最大化是核心思想，因为它有助于找到一个最优的超平面，这个超平面不仅可以将数据正确分类，而且具有最大的泛化能力。

对于任意一点 $x_i$，其到超平面 $w\cdot x+b=0$ 的距离 $d_i$ 可以用以下公式表示：
$$d_i=\frac{|w\cdot x_i+b|}{\Vert w\Vert }$$
其中：

1. $\Vert w\Vert$ 是 $w$ 的 $L_2$ 范数（即欧几里得长度）。

间隔 $\text{margin}$ 则是所有样本点中距离超平面最近的点到超平面的距离的两倍：
$$\text{margin}=2\times \underset{i}{\min }{d}_i=2\times \underset{i}{\min }\left(\frac{|w\cdot x_i+b|}{\Vert w\Vert }\right)$$

从间隔的公式可以看出，当 $w$ 的范数 $\Vert w\Vert$ 减小时，间隔 $\text{margin}$ 会增大。这是因为分母