Python在高等数学和线性代数中的应用

from sympy import *
x,y,z=symbols('x  y  z')
m0,m1,m2,m3=symbols('m0:4')  #创建多个符号变量
x=sin(1)
print("x=",x); 
print("x=",x.evalf())
print("x=",x.n(16))  #显示小数点后16位数字
print("pi的两种显示格式:{},{}".format(pi,pi.evalf(3)))  #这里不能使用n()函数
expr1=y*sin(y**2)  #创建第一个符号表达式
expr2=y**2+sin(y)*cos(y)+sin(z)  #创建第二个符号表达式
print("expr1=",expr1)
print("y=5时，expr1=",expr1.subs(y,5))  #代入一个符号变量的值
print("y=2,z=3时，expr2=",expr2.subs({y:2,z:3}))  #代入y=2,z=3
print("y=2,z=3时，expr2=",expr2.subs({y:2,z:3}).n())  #以浮点数显示计算结果

together和apart方法使用示例如下：

from sympy import *
x1,x2,x3,x4=symbols('m1:5'); x=symbols('x')
print(x1/x2+x3/x4)
print(together(x1/x2+x3/x4))#展开
print((2*x**2+3*x+4)/(x+1))
print(simplify((2*x**2+3*x+4)/(x+1)))  #化简没有效果
print(apart((2*x**2+3*x+4)/(x+1)))

1.2 用SymPy做符号函数画图

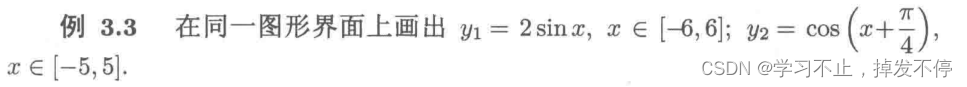
from sympy.plotting import plot
from sympy.abc import x , pi
from sympy.functions import sin,cos

plot((2*sin(x),(x,-6,6)),(cos(x + pi/4),(x,-5,5)))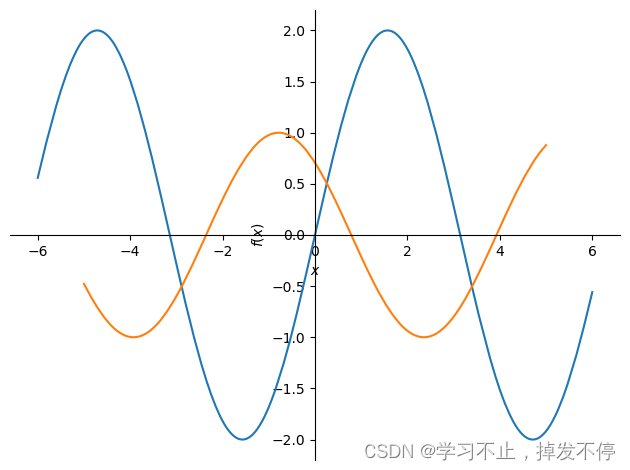

from sympy.plotting import plot3d
from sympy.abc import x , pi
from sympy.functions import sin,sqrt

plot3d(sin(sqrt(x**2 + y**2)),(x,-10,10),(y,-10,10),xlabel = '$x$',ylabel = '$y$')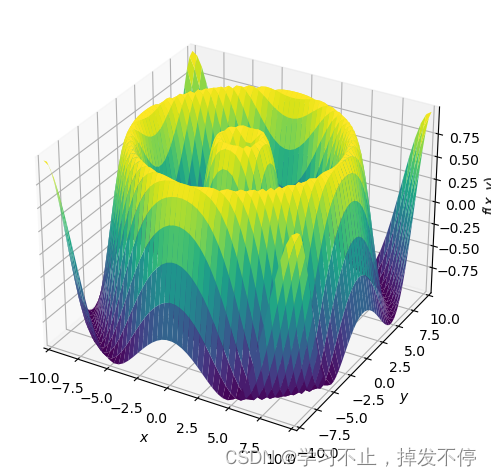

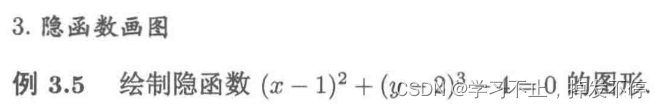
from sympy import plot_implicit as pt,Eq
from sympy.abc import x,y
pt(Eq((x-1)**2 + (y-2)**3,4),(x,-6,6),(y,-4,4),xlabel = '$x$',ylabel = '$y$')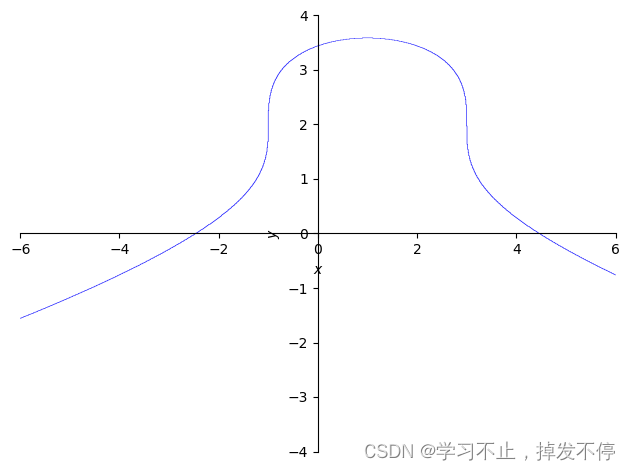

2. 高等数学的符号解

2.1 极限

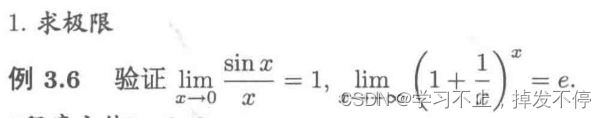
求极限用limit()

from sympy import *
x = symbols('x')
print(limit(sin(x)/x,x,0))#求出1
print(limit((1 + 1/x)**x,x,oo))#求出e

2.2 导数

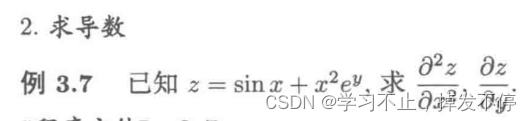
求导数用diff()

from sympy import *
x,y = symbols('x y')
z = sin(x) + x**2 * exp(y)
#二阶偏导数
print(diff(z,x,2))#求出2*exp(y) - sin(x)
#一阶偏导数
print(diff(z,y))#求出x**2*exp(y)

2.3 级数求和

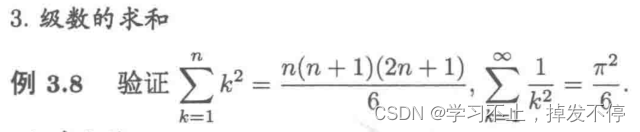
factor可以把计算结果因式分解，级数求和用summation

from sympy import*
k,n=symbols ('k n')
print(summation(k**2, (k, 1,n)))#n**3/3 + n**2/2 + n/6
print(factor(summation(k**2, (k, 1,n))))#n*(n + 1)*(2*n + 1)/6
print(summation(1/k**2,(k,1,oo)))#pi**2/6

最低0.47元/天解锁文章