MIT-OC Electrochemical Energy Systems4-2

四、输运现象

L17 燃料电池中的强制对流(1)

目录

1. 膜电极组件
2. 一般分析
   • 2.1 达西定律
   • 2.2 对流扩散方程
   • 2.3 边界条件
3. 尺度分析
   • 3.1 消耗层厚度的尺度分析
   • 3.2 Peclet数和Sherwood数
   • 3.3 极限电流
4. 相似解
5. 总结
6. 补充—主导平衡法分析对流和扩散过程

1. 膜电极组件

膜电极组件用于产生对流流动，以便更有效地将反应物传输到催化剂层。反应气体被迫通过入口通道进入，并通过单独的出口通道排出。这些气体必须穿过多孔电极才能到达催化剂层。

1.1 组装示意

膜电极组件设计了交替的进出口通道，从而使气体被迫通过多孔电极，进而更好地与催化剂层接触并参与反应。

图 1：膜电极组件

图 2：交叉指状流道

2. 一般分析

对流速度和压力梯度之间的关系可以通过达西定律表示，而浓度随对流和扩散共同作用的变化可以通过对流-扩散方程来描述。

2.1 达西定律

对流速度 $u$ 与压力梯度之间的关系通过达西定律描述为：
$$u=-K\nabla p$$
其中，$K$ 是流体的渗透率，是一个常数。

2.2 对流扩散方程

对于不可压缩流体，通量满足以下方程：
$$\nabla \cdot u=0$$
结合达西定律，可以得到：
$${\nabla }^{2}p=0$$

要保持稳态，总浓度的变化速率由于对流和扩散的共同作用必须为零【对流扩散方程】，因此：
$$u\cdot \nabla c=D{\nabla }^{2}c$$
代入达西定律，得到：
$$-K\nabla p\cdot \nabla c=D{\nabla }^{2}c$$

2.3 边界条件

• 入口和出口：压力和浓度是固定的。入口压力为 $p_{in}$，出口压力为 $p_{out}$，浓度两者相同为 $c_0$。
• 壁面：无速度通过壁面，即 $n\cdot \nabla p=0$，而且 $n\cdot \nabla c=0$。
• 膜面：在膜上，压力梯度和通过膜的扩散通量都为零，但反应速率 $R$ 与扩散通量必须相等，且在极限电流条件下，$c=0$。【扩散的全部反应掉】

图 3：平衡状态下的流量剖面

3. 尺度分析

3.1 消耗层厚度的尺度分析

对于在吸收表面上浓缩液体的恒速流动，形成了一个消耗层。消耗层的厚度 $\delta (x)$ 如下图所示。

该过程由对流-扩散方程描述：
$$u\frac{\partial c}{\partial x}=D\left(\frac{{\partial }^{2}c}{\partial x^2}+\frac{{\partial }^{2}c}{\partial y^2}\right)$$
通过主导平衡法【详细推导见文末补充】处理该问题，在距离吸收器开始较远的地方，对流在 $x$ 方向上占主导地位，而浓度沿 $y$ 方向的变化较快，因此：
$$u\frac{\partial c}{\partial x}\approx D\frac{{\partial }^{2}c}{\partial y^2}$$
我们可以估算这些项的大小，得到：
$$\frac{c_0}{x}\sim \frac{D{c}_0}{{\delta }^2}$$
从而可以求出消耗层厚度 $\delta$：
$$\delta \sim \sqrt{\frac{Dx}{u}}$$

图 4：通过保形映射解决对流扩散问题

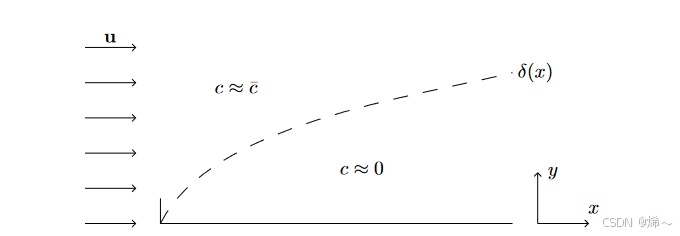
图 5：对流扩散边界层厚度

3.2 Peclet数和Sherwood数

为了便于描述，我们引入无量纲变量。通过将 $\delta$ 和 $x$ 分别除以流动流体的高度 $H$，可以得到：
$$\tilde{\delta }\sim \sqrt{\frac{\tilde{x}}{Pe}}$$
其中，Peclet数定义为：
$$Pe=\frac{uH}{D}$$

通量密度 $R$ 为：
$$R=D\frac{\partial c}{\partial y}$$
可以进一步得到无量纲形式的通量，称为 Sherwood 数 $Sh$：
$$Sh\sim \sqrt{Pe\tilde{x}}$$

3.3 极限电流

极限电流是通过吸收面上的通量积分乘以每次吸收反应中传递的电荷得到的。如果吸收面宽度为 $W$，长度为 $L$，则极限电流为：
$$I_{lim}\sim neW{c}_0\sqrt{uDL}$$
将其无量纲化后得到：
$${\tilde{I}}_{lim}\sim \sqrt{Pe\frac{H}{L}}$$
因此可以通过增加流速来提高极限电流。
存在一个权衡：所使用的燃料的比例。如果我们将 γF 定义为消耗的燃料与燃料输入的比率，我们发现

$$\begin{array}{rl}{\gamma }_F& =\frac{I_{lim}}{neuHW\bar{c}}\\ & \sim \frac{1}{\sqrt{\text{Pe}H/L}}\\ & \sim \frac{1}{{\tilde{I}}_{lim}}.\end{array}$$

因此我们看到，即使可以增加限制电流，但这也会导致燃料利用率相应下降。

4. 相似解

除了尺度分析，还可以通过相似解精确地求解对流-扩散方程。如果定义 $\tau =x/u$，则可以将原方程简化为扩散方程：
$$\frac{\partial c}{\partial \tau }=D\frac{{\partial }^{2}c}{\partial y^2}$$
该方程的边界条件为 $c(y,0)=c_0$，$c(0,\tau )=0$，相似解形式为：
$$c(y,\tau )=c_0\text{erf}\left(\frac{y}{2\sqrt{D\tau }}\right)$$
通量可以求得为：
$$R=\frac{c_0\sqrt{uD}}{\sqrt{\pi x}}$$
与之前的近似结果相比，精确求解仅多了一个因子 $1/\sqrt{\pi }$。

5. 总结

1. 强制对流可以有效提高燃料电池中的极限电流，克服仅通过扩散传质的限制。
2. 通过达西定律和对流-扩散方程，可以建立流体流动与浓度变化之间的关系。
3. 使用尺度分析可以近似得出消耗层厚度和极限电流的表达式，Peclet数和Sherwood数在描述这些现象中起到了重要作用。
4. 相似解可以精确求解对流-扩散方程，从而更准确地描述反应物浓度的分布。

6. 补充——主导平衡法分析对流和扩散过程

在该问题中，我们应用主导平衡法来分析对流和扩散过程的相对重要性，主要目的是确定在哪些情况下某些过程可以忽略不计。这也是化学工程和流体动力学中一种常用的分析方法。

为什么对流在 (x) 方向上占主导地位，而浓度沿 (y) 方向的变化较快？

1. 系统几何特性：

   • 在吸收器中，流体从入口流动到出口，沿着吸收表面的流动方向被设定为 (x) 方向。这个方向上的流动是主流方向，通常具有显著的速度 (u)，即对流速度。
   • 而在 (y) 方向（垂直于流动方向），浓度的变化主要是由扩散引起的。因为流体本身的速度主要是在 (x) 方向上，所以在 (y) 方向上的速度接近于零。因此，浓度的变化只能依靠扩散来进行。

2. 对流占主导地位的区域：

   • 随着流体在吸收器中的流动，反应物质不断被吸收，导致浓度在 (y) 方向上逐渐减少。
   • 在距离吸收器开始较远的地方，流体已经经历了一段较长的流动距离，因此在 (x) 方向上，浓度的变化是较慢的。换句话说，沿流动方向（(x) 方向）上的浓度梯度通常较小，相比之下，对流的影响变得更加显著。

3. 扩散和对流之间的竞争：

   • 在 (x) 方向上，对流的特征是速度高而稳定，意味着反应物质随流体一起流动，不需要依赖于浓度梯度的扩散来进行传输。
   • 然而，在垂直方向（(y) 方向），反应物质需要从流体主体扩散到吸收表面才能参与反应。因此，浓度梯度在 (y) 方向上非常陡峭，导致该方向上的变化速率较快，表现为浓度沿 (y) 方向的变化显著。

4. 尺度分析的结果：

   • 从尺度分析来看，对流-扩散方程中的两个主导项分别是对流项 $u\frac{\partial c}{\partial x}$和扩散项 $D\frac{{\partial }^{2}c}{\partial y^2}$。由于 (u) 通常远大于扩散系数 (D)，并且流动方向的特征长度（(x)）通常也大于垂直方向的扩散长度（$\delta$），对流项在 (x) 方向占据主导地位，而浓度的变化在 (y) 方向上占主导地位。
   • 这也是为什么我们可以近似地认为：在距离吸收器开始较远的地方，对流在 (x) 方向占主导地位，而浓度在 (y) 方向的变化更快。