Reward-Guided Speculative Decoding for Efficient LLM Reasoning
Speculative Decoding的不足
speculative decoding虽然可以加速LLM inference,其要求严格的无偏性,这在概率上和target model完全一致,理论上不会降低生成质量,但是由于严格无偏性的条件过于苛刻,这会导致draft model生成的一些高质量的token即使正确,由于分布差异或概率稍低而被拒绝,进而造成额外的target model的调用代价,这个问题在复杂推理中更为严重。
RSD概括
RSD的核心想法:放宽draft model 生成内容的接受条件,允许有偏接受策略。
具体而言,通过引入一个process reward model,以reward作为接受/拒绝的条件,而不是严格按照概率分布匹配。
这样做的好处也很显然,生成内容接受条件放宽必然带来更多token的接受,进而减少target model调用的次数,同时有process reward model的监督也能保证生成质量。
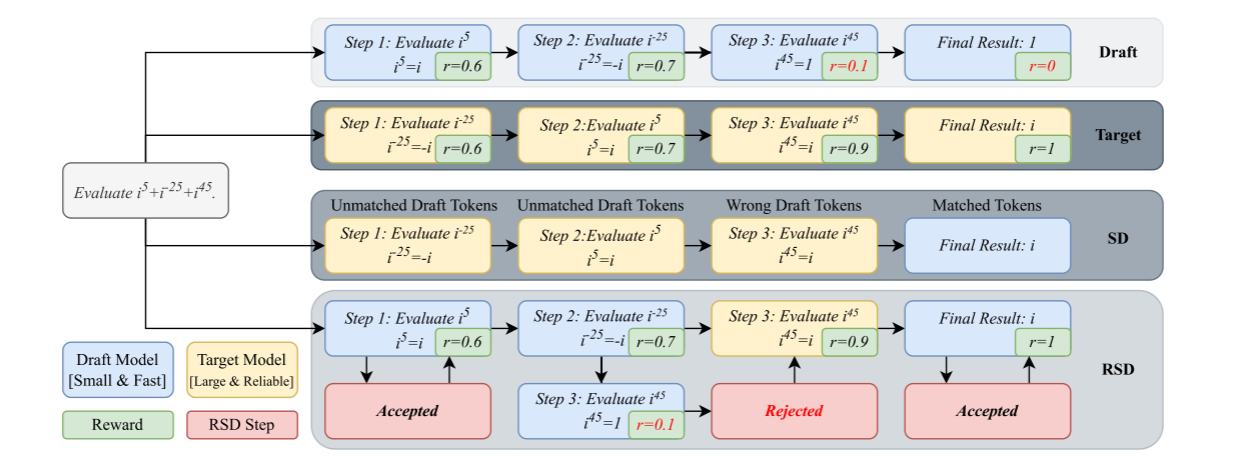
这张图可以分为上下两部分看,上半部分是传统Speculative Decoding,下半部分是论文提出的RSD
可以看到上半部分对于draft model生成的每一份draft,都需要调用target model进行验证,而下半部分RSD则是根据reward决定是否调用target model进行生成。
具体细节
RSD算法流程
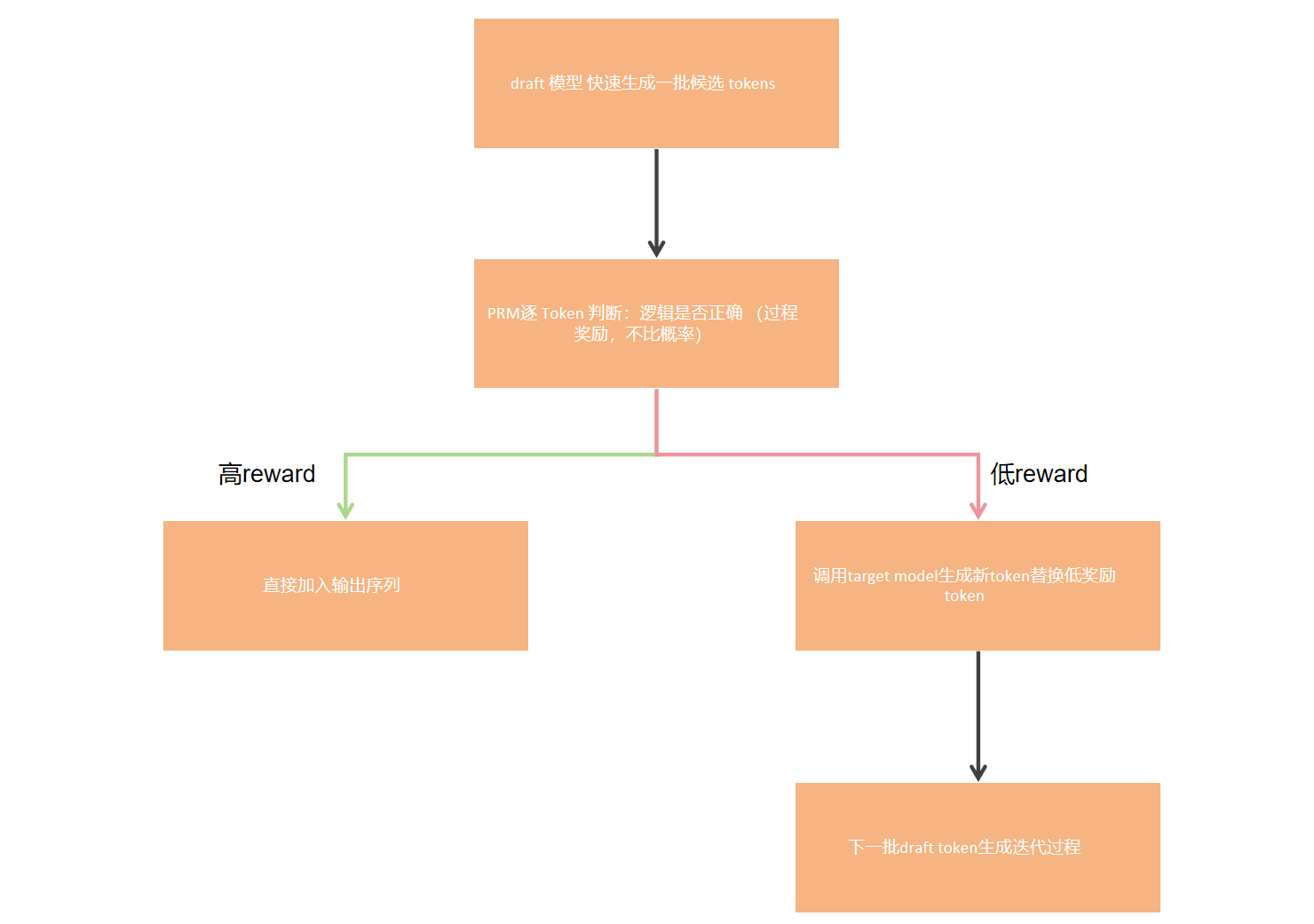

token接受
token接受的reward阈值。
这里是通过一个
ω
(
⋅
)
\omega(\cdot)
ω(⋅)的权重函数,将reward映射到
[
0
,
1
]
[0,1]
[0,1],进而可以使用采样方法。
w
(
y
i
∣
z
i
)
=
ω
r
(
y
i
∣
z
i
)
=
ω
(
r
(
y
i
∣
z
i
)
)
w(y_i \mid z_i) = \omega_r(y_i \mid z_i) = \omega(r(y_i \mid z_i))
w(yi∣zi)=ωr(yi∣zi)=ω(r(yi∣zi))

算法2,这里对于
ω
(
⋅
)
\omega(\cdot)
ω(⋅)允许多种实现方式,如阶跃函数或更平滑的函数
对于不同的权重函数作者也讨论了不同实现的好处,同时在table1中给出了不同的权重函数。
- 对于阶跃函数在理论上最优
- 对于其他函数则更加平滑

这里二元阶跃函数是最优的。
RSD概率分布理论分析
进行相关符号的规定:
| 符号 | 内容 |
|---|---|
| x ∈ R l × d x \in \mathbb{R}^{l \times d} x∈Rl×d | prompt |
| y ∈ R L × d y \in \mathbb{R}^{L \times d} y∈RL×d | reponse |
| y 1 : n y_{1:n} y1:n | [ y 1 , . . . , y n ] [y_1,...,y_n] [y1,...,yn] |
| z i z_i zi | [ x , y 1 : i − 1 ] [x,y_{1:i-1}] [x,y1:i−1] |
| m | draft model |
| M | target model |
| P m ( y i ∣ z i ) P_m(y_i|z_i) Pm(yi∣zi) | the distribution of draft model sample |
| P M ( y i ∣ z i ) P_M(y_i|z_i) PM(yi∣zi) | the distribution of target model sample |
| r ( y i ∣ z i ) = r ( y i ∣ x , y 1 : i − 1 ) r(y_i|z_i)=r(y_i|x,y_{1:i-1}) r(yi∣zi)=r(yi∣x,y1:i−1) | reward function |
较高的奖励值
r
(
y
i
∣
z
i
)
r(y_i \mid z_i)
r(yi∣zi) 表示,在给定输入
x
x
x 和之前已生成的步骤
y
1
:
i
−
1
y_{1:i-1}
y1:i−1 的情况下,该模型输出与期望的响应更契合的可能性更大。
所以target model M的expect reward应该是大于draft model m
E
y
i
∼
P
M
[
r
(
y
i
∣
z
i
)
]
≥
E
y
i
∼
P
m
[
r
(
y
i
∣
z
i
)
]
,
(
1
)
\mathbb{E}_{y_i \sim \mathbf{P}_M}[r(y_i|z_i)] \geq \mathbb{E}_{y_i \sim \mathbf{P}_{m}}[r(y_i|z_i)], \quad (1)
Eyi∼PM[r(yi∣zi)]≥Eyi∼Pm[r(yi∣zi)],(1)
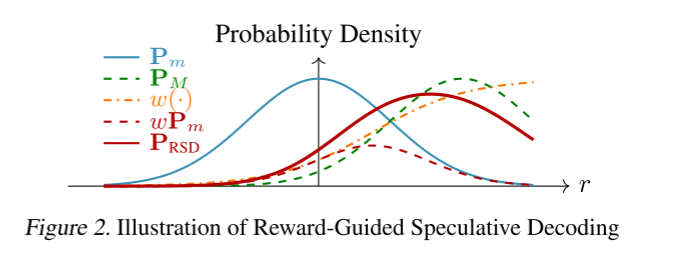
理论分析所提出方法的RSD的分布
P
R
S
D
P_{RSD}
PRSD,其由
P
m
、
P
M
P_m、P_M
Pm、PM结合
P
R
S
D
(
y
i
∣
z
i
)
=
w
(
y
i
∣
z
i
)
P
m
(
y
i
∣
z
i
)
+
v
(
y
i
∣
z
i
)
P
M
(
y
i
∣
z
i
)
\mathbf{P}_{\mathrm{RSD}}(y_i \mid z_i) = w(y_i \mid z_i) \mathbf{P}_m(y_i \mid z_i) + v(y_i \mid z_i) \mathbf{P}_M(y_i \mid z_i)
PRSD(yi∣zi)=w(yi∣zi)Pm(yi∣zi)+v(yi∣zi)PM(yi∣zi)
其中
w
(
y
i
∣
z
i
)
w(y_i \mid z_i)
w(yi∣zi)是一个权重函数根据draft model输出的reward动态调整,而
v
(
y
i
∣
z
i
)
v(y_i \mid z_i)
v(yi∣zi)是一个常量,这保证了target model永远都有一部分参与,不至于完全依赖draft model出现断层,换句话始终有target model来兜底。
其他
只有在target model显著大于PRM时这个方法的效果才会比较明显,因为这里虽然减少了target model的验证步,但是引入了新的开销,PRM获得reward。























 1589
1589

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








