一、 指数加权平均 EWA|EMA
指数加权平均是一种对时间序列数据进行平滑处理的一种方法,思想主要是:
越近的数据权重越大,越远的数据权重越小,且权重呈指数衰减
definite:给定一个时间序列
x
1
,
x
2
,
x
3
,
.
.
.
,
x
t
x_1, x_2, x_3, ...,x_t
x1,x2,x3,...,xt,其指数加权
v
t
v_t
vt定义为
v
0
=
0
v
t
=
β
v
t
−
1
+
(
1
−
β
)
x
t
v
t
=
(
1
−
β
)
(
x
t
+
β
x
t
−
1
+
β
2
x
t
−
2
+
β
3
x
t
−
3
+
.
.
.
)
v_0=0\\v_t=\beta v_{t-1}+(1 - \beta)x_t \\v_t=(1-\beta)(x_t+\beta x_{t-1}+\beta^2 x_{t-2} + \beta^3 x_{t-3} + ...)
v0=0vt=βvt−1+(1−β)xtvt=(1−β)(xt+βxt−1+β2xt−2+β3xt−3+...)
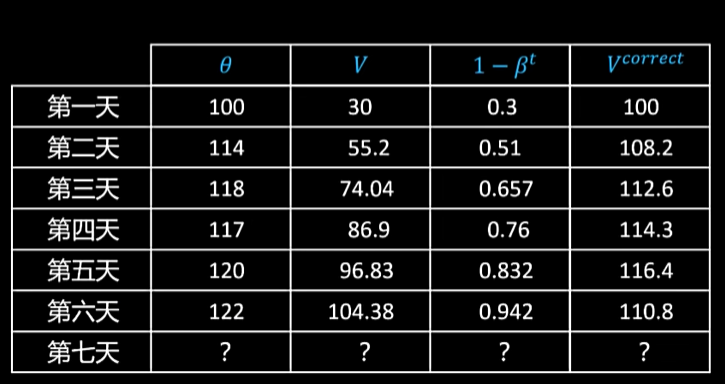
可以看到当
v
0
=
0
,
β
=
0.7
v_0=0, \beta=0.7
v0=0,β=0.7时计算的结果偏小,这是由于
v
0
v_0
v0初始化为0的缘故,这里可以对V进行修正
V
t
c
o
r
r
e
c
t
=
V
t
1
−
β
t
V_t^{correct}=\frac{V_t}{1-\beta^t}
Vtcorrect=1−βtVt
二、 SGD
如图是损失函数g的等高线
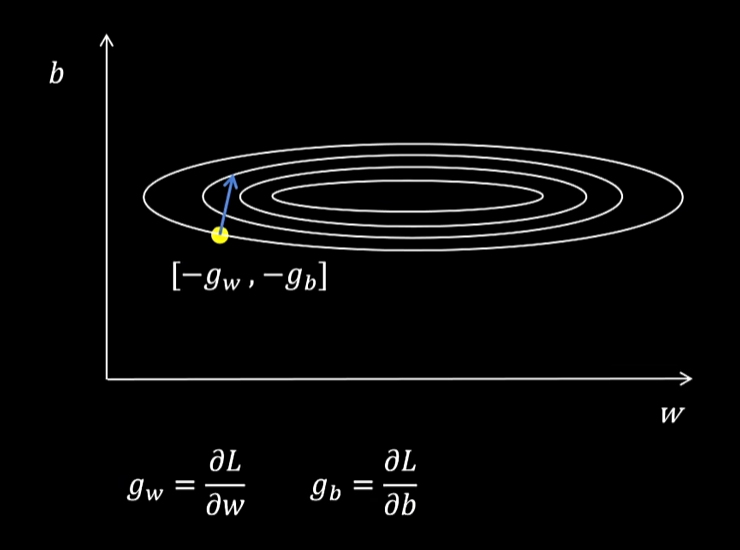
sgd更新啊权重仅仅取决于当前梯度,这样可能会导致训练震荡不稳定。
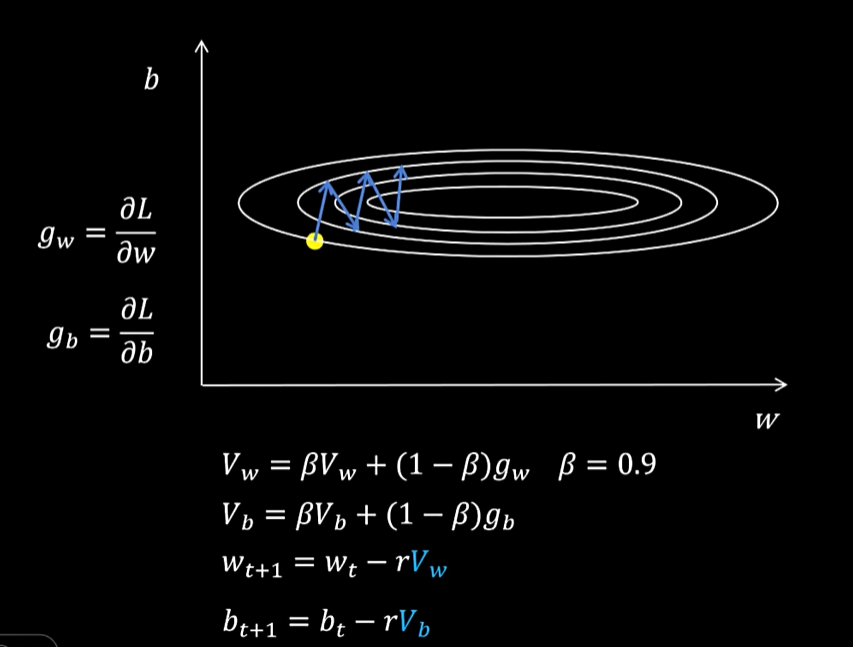
三、 Momentum
如果不是用当前梯度去更新参数,而是用梯度的指数加权平均去更新,这样加入指数平均可以减少异常数据的影响。
四、 RMSProp
RMSProp解决的问题是在不同方向上梯度不同的问题导致的震荡,因为所有方向共享一个学习率,这就导致在平稳方向参数更新缓慢,而在陡峭方向上,参数更新又会比较剧烈从而发生震荡。
RMSProp是对AdaGrad的基础上改进的,AdaGrad为每个参数维护了一个历史梯度平方和
G
t
=
∑
i
=
1
t
g
i
2
G_t=\sum_{i=1}^{t}g_i^2
Gt=∑i=1tgi2,用历史梯度平方和来自适应调整学习率
θ
t
+
1
=
θ
t
−
α
G
t
+
ϵ
⊙
g
t
\theta_{t+1}=\theta_{t}-\frac{\alpha}{\sqrt{G_t+\epsilon}}\odot g_t
θt+1=θt−Gt+ϵα⊙gt
而RMSProp对AdaGrad的改进体现在位于梯度平方的维护上使用指数加权平均,仅让最近的梯度平方参与学习率的修正。
v
t
=
β
v
t
−
1
+
(
1
−
β
)
g
t
2
θ
t
+
1
=
θ
t
−
α
v
t
+
ϵ
g
t
v_t=\beta v_{t-1} + (1-\beta)g_t^2\\\theta_{t+1} = \theta_t - \frac{\alpha}{\sqrt{v_t+\epsilon}}g_t
vt=βvt−1+(1−β)gt2θt+1=θt−vt+ϵαgt
五、 Adam
Adam算法就是将Mountum算法和RMSProp算法结合起来,并对指数加权平均值进行修正。
g
w
=
∂
L
∂
w
V
w
=
β
1
V
w
+
(
1
−
β
1
)
g
w
,
β
1
=
0.9
S
w
=
β
2
S
w
+
(
1
−
β
2
)
g
w
2
,
β
2
=
0.999
V
w
c
o
r
r
e
c
t
=
V
w
1
−
β
1
t
S
w
c
o
r
r
e
c
t
=
S
w
1
−
β
2
t
w
t
+
1
=
w
t
−
α
S
w
c
o
r
r
e
c
t
+
ϵ
V
w
c
o
r
r
e
c
t
g_w=\frac{\partial L}{\partial w} \\V_w=\beta_1V_w+(1-\beta_1)g_w,\beta_1=0.9\\ S_w=\beta_2 S_w + (1-\beta_2)g_w^2,\beta_2=0.999\\ V_w^{correct}=\frac{V_w}{1-\beta_1^t}\\ S_w^{correct}=\frac{S_w}{1-\beta^t_2}\\ w_{t+1} = w_t - \frac{\alpha}{\sqrt{S_w^{correct}}+\epsilon}V_w^{correct}
gw=∂w∂LVw=β1Vw+(1−β1)gw,β1=0.9Sw=β2Sw+(1−β2)gw2,β2=0.999Vwcorrect=1−β1tVwSwcorrect=1−β2tSwwt+1=wt−Swcorrect+ϵαVwcorrect
六、 AdamW
AdamW是在AdamW上做了一点改动就是在更新参数时进行了weight decay,具体weight decay 参考链接Weight decay 和 L2 Regularization,用一句话就是在更新参数是减去一个值,防止参数过大,提高模型的泛化性。
g
w
=
∂
L
∂
w
V
w
=
β
1
V
w
+
(
1
−
β
1
)
g
w
,
β
1
=
0.9
S
w
=
β
2
S
w
+
(
1
−
β
2
)
g
w
2
,
β
2
=
0.999
V
w
c
o
r
r
e
c
t
=
V
w
1
−
β
1
t
S
w
c
o
r
r
e
c
t
=
S
w
1
−
β
2
t
w
t
+
1
=
w
t
−
α
S
w
c
o
r
r
e
c
t
+
ϵ
V
w
c
o
r
r
e
c
t
−
r
λ
w
t
g_w=\frac{\partial L}{\partial w} \\V_w=\beta_1V_w+(1-\beta_1)g_w,\beta_1=0.9\\ S_w=\beta_2 S_w + (1-\beta_2)g_w^2,\beta_2=0.999\\ V_w^{correct}=\frac{V_w}{1-\beta_1^t}\\ S_w^{correct}=\frac{S_w}{1-\beta^t_2}\\ w_{t+1} = w_t - \frac{\alpha}{\sqrt{S_w^{correct}}+\epsilon}V_w^{correct}-r \lambda w_t
gw=∂w∂LVw=β1Vw+(1−β1)gw,β1=0.9Sw=β2Sw+(1−β2)gw2,β2=0.999Vwcorrect=1−β1tVwSwcorrect=1−β2tSwwt+1=wt−Swcorrect+ϵαVwcorrect−rλwt
七、 总结
Adam、和AdamW都是需要对每个参数维护两个相关的量一个保存梯度的指数平均,一个保存指数平方的指数平均,如果参数是用float16进行存储,由于一般梯度的数值都比较小,需要使用float32来存储,那么这两个值占用的大小是参数大小的4倍。
本文参考视频十分钟搞明白Adam和AdamW,SGD,Momentum,RMSProp,Adam























 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








