链接入口:【西瓜书真的不适合所有人!】同济大佬半天就教会了我12大机器学习算法,回归算法、支持向量机、决策树随机森林等,一次学到爽!_哔哩哔哩_bilibili
如果该链接失效,可在b站上找相同的视频不同的发布者
概述
大数据时代造就人工智能的高速发展。
机器学习中包含神经网络,神经网络扩展后造就深度学习算法
效果

深度学习能够述说图片的故事,无人驾驶汽车,图像融合
计算机视觉
图像
概述
一张图片会被表示成三维数组形式,例如:300*100*3,表示长*宽*颜色通道(【R,G,B】红,绿,蓝。颜色通道为3表示是彩色图,为1表示是灰色图)
像素点的值0-255,值与亮度挂钩。
影响因素
拍摄角度,光照强度,形状改变,部分遮蔽(重要),背景混入
常规套路
1、收集数据并给定标签
2、训练一个分类器
3、测试,评估
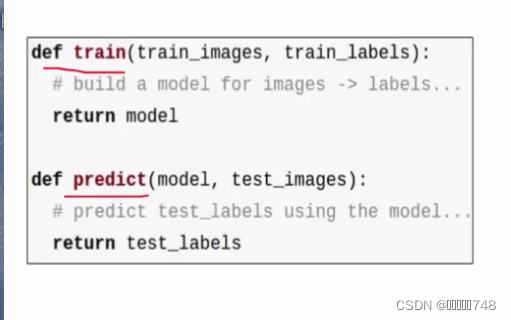
分类
K-近邻算法

概述:设定k值,找出离所求点最近的k个值,所求点的值等于数量最多的值。
不需要训练,训练复杂度为0,分类计算复杂度与训练集的文档数成正比。
练手数据集:CIFAR-10
计算方法

代码

使用交叉验证进行模型建立:

背景主导:背景很大程度上影响了分类的效果,所以不使用k近邻进行分类
神经网络
线性分类
概述

W表示一些权重参数
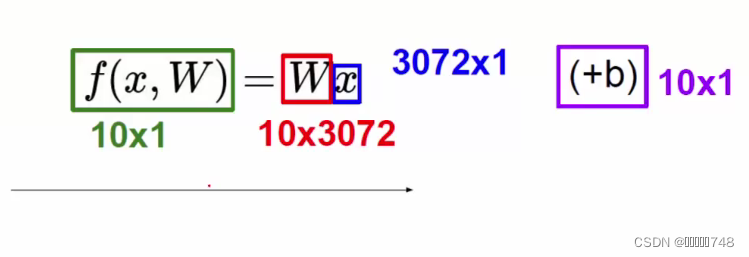
10表示的是有的类别,x表示的是图像的像素点,b是定义的类别数*1的矩阵
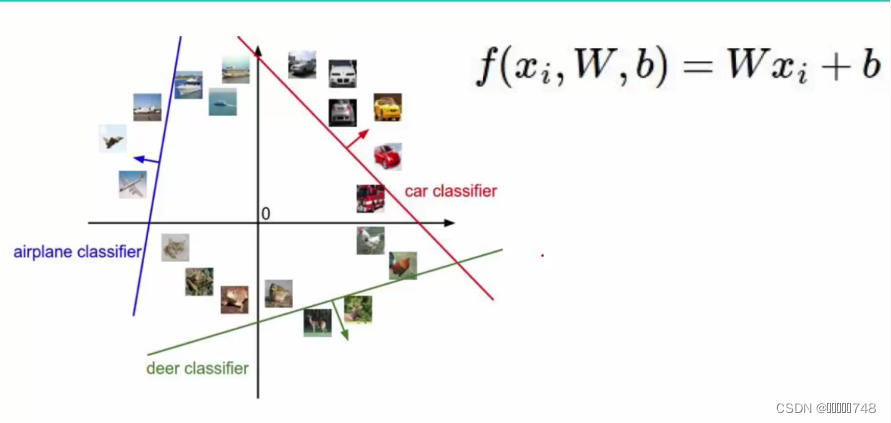
损失函数
作用:评估当前的模型的效果
判断标准:若损失函数算出来大于0,则有损失,若小于0,则无损失,直接令值为0。效果最好时,损失函数为0,损失函数值越大,表示该模型效果越差。
举例:
正则化惩罚项
平方
最终函数表达式

Softmax分类器
关键:将得分值转化为概率值

Sigmoid函数
损失函数:计算损失值
总结

最优化
找出最好的参数:通过梯度下降的方向求解角度
前向传播
梯度下降算法


每次迭代都会修正w
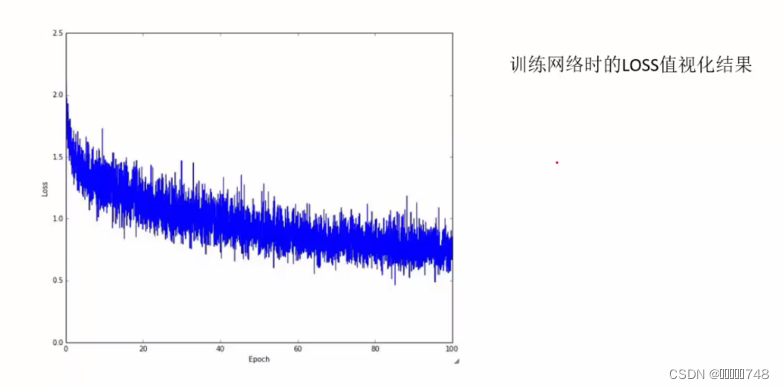
Epoch:跑完所有图像,称为一次Epoch
迭代:完成Bachsize所设置数量的图像的前向传播和反向传播
学习率
概率:让网络模型自己学习
学习率通常设置小一点,例如0.001或者0.0001

反向传播


加法门单位:均等分配
MAX门单元:给最大的
乘法门单元:互换的感觉
神经网络结构
神经网络永远都不会收敛
神经元

在每一层后面加一层激活函数,会使得神经网络的效果更好。

激活函数
1、
非线性函数,负无穷接近于0,正无穷接近于1
梯度消失现象太严重

2、
首选
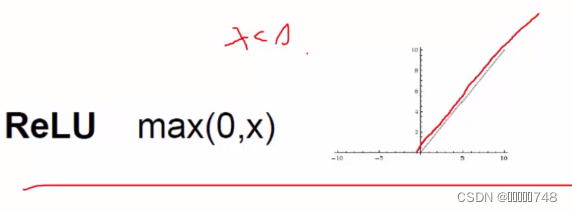
神经网络

一定范围内神经元的数量越多效果越好,越能表达复杂的模型,但是如果过多,会导致过拟合。
神经元就是权重参数
过拟合解决方案
正则化项在神经网络中的重要作用

数据预处理
zero-centered datacenter数据中心化
每个样本减去均值
normalized data归一化
以0为均值,所有值都在0-1区间
权重初始化
随机初始化
w=0.01*np.random.randn(D,H)
D,H是矩阵
关于b
零值初始化或者1初始化
drop-out
全连接会导致过拟合
随机选择神经元效果更好

#初始化w和b
w=0.01*np.random.randn(D,K)
b=np.zeros(1,K)
#加上正则化惩罚项
step_size=le-0
reg=le-3
#
num_examples=X.shape[0]
for i in xrange(1000):
scores=np.dot(X,W)+b #先进行前向传播
exp_scores=np.exp(scores)
probs=exp_scores/np.sum(exp_scores,axis=1,keepdims=True)#对得分值进行归一化操作,将得分值转化为概率值
corect_logprobs=-np.log(probs[range(num_examples),y])#计算log值
#进行反向传播
data_loss=np.sum(corect_logprobs)/num_examples
reg_loss=0.5*reg*np.sum(W*W)
loss=data_loss+reg_loss
if i %100==0:
print"iteration %d:loss %f"%(i,loss)
dscores=probs
dscores[range(num_examokes),y]-=1
dscores /=num_examples
dW=np.dot(X.T,dscores)
db=np.sum(dscores,axis=0,keepdims=True)
dW+=reg*WPCA降维
找出具有代表性的特征
#对特征进行标准化
from sklearn.preprocessing import StandardScaler
X_std=StandardScaler().fit_transform(X)
print(X_std)看指标
协方差:

#计算均值
mean_vec=np.mean(X_std,axis=0)
#创建协方差矩阵
#法一
cov_mat=(X_std-mean_vec).T.dot((X_std-mean_vec))/(X_std.shape[0]-1)
print('Covariance matrix \n%s' %cov_mat)
#法二
print('NumPy covariance matrix: \n%s' %np.cov(X_std.T))
#计算特征值eig_vals和特征向量eig_vecs
cov_mat=np.cov(X_std.T)
eig_vals,eig_vecs=np.linalg.eig(cov_mat)
#进行归一化
#cumsum函数每一个值等于前面所有值的和
tot=sum(eig_vals)
var_exp=[(i/tot)*100 for i in sorted(eig_vals,reverse=True)]
print(var_exp)
cum_var_exp=np.cumsum(var_exp)
cum_var_exp降维为多少维度看特征值的大小
matrix_w=np.hstack((eig_pairs[0][1].reshape(4,1),eig_pairs[1][1].reshape(4,1)))
#进行降维操作
Y=X_Std.dot(matrix_w)






 本文介绍了机器学习的基础,包括K-近邻算法、神经网络的线性分类和Softmax分类器。讨论了深度学习在图像识别中的应用,如图像分类,并深入讲解了神经网络的训练过程,如梯度下降和反向传播。同时,提到了防止过拟合的方法,如正则化和Dropout,并探讨了数据预处理和PCA降维的重要性。
本文介绍了机器学习的基础,包括K-近邻算法、神经网络的线性分类和Softmax分类器。讨论了深度学习在图像识别中的应用,如图像分类,并深入讲解了神经网络的训练过程,如梯度下降和反向传播。同时,提到了防止过拟合的方法,如正则化和Dropout,并探讨了数据预处理和PCA降维的重要性。
















 5598
5598

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








